Sphere with Shells
This section presents a model composed of a sphere with two concentric shells. We use the model to explore answers to the following questions:
- What compute time is required to create successively refined resolutions in
automesh? - What compute time is required to create these same resolutions in Sculpt?
- Given a rotational boundary condition, what are the displacement and strain fields for the voxel mesh?
- How do the results for the voxel mesh compare with the results for a conforming mesh?
- To what degree may smoothing the voxel mesh improve the results?
- To what degree may dualization of the voxel mesh improve the results?
Model
Python is used to create a segmentations, saved as .npy files, and visualize the results.
Given
Given three concentric spheres of radius 10, 11, and 12 cm, as shown in the figure below,
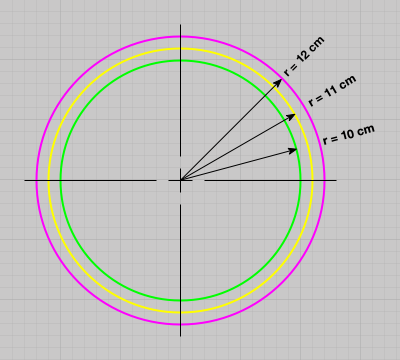
Figure: Schematic cross-section of three concentric spheres of radius 10, 11, and 12 cm. Grid spacing is 1 cm.
Find
Use segmentation resolutions 1, 2, 4, and 10 voxels per centimeter
with a cubic domain (nelx = nely = nelz) to create finite element meshes.
Solution
| vox/cm | element side length (cm) | nelx | # voxels | segmentation | file size |
|---|---|---|---|---|---|
| 1 | 1.0 | 24 | 13,824 | spheres_resolution_1.npy | 14 kB |
| 2 | 0.5 | 48 | 110,592 | spheres_resolution_2.npy | 111 kB |
| 4 | 0.25 | 96 | 884,736 | spheres_resolution_3.npy | 885 kB |
| 10 | 0.1 | 240 | 13,824,000 | spheres_resolution_4.npy | 13.78 MB |
Python Segmentation
The Python code used to generate the figures is included below.
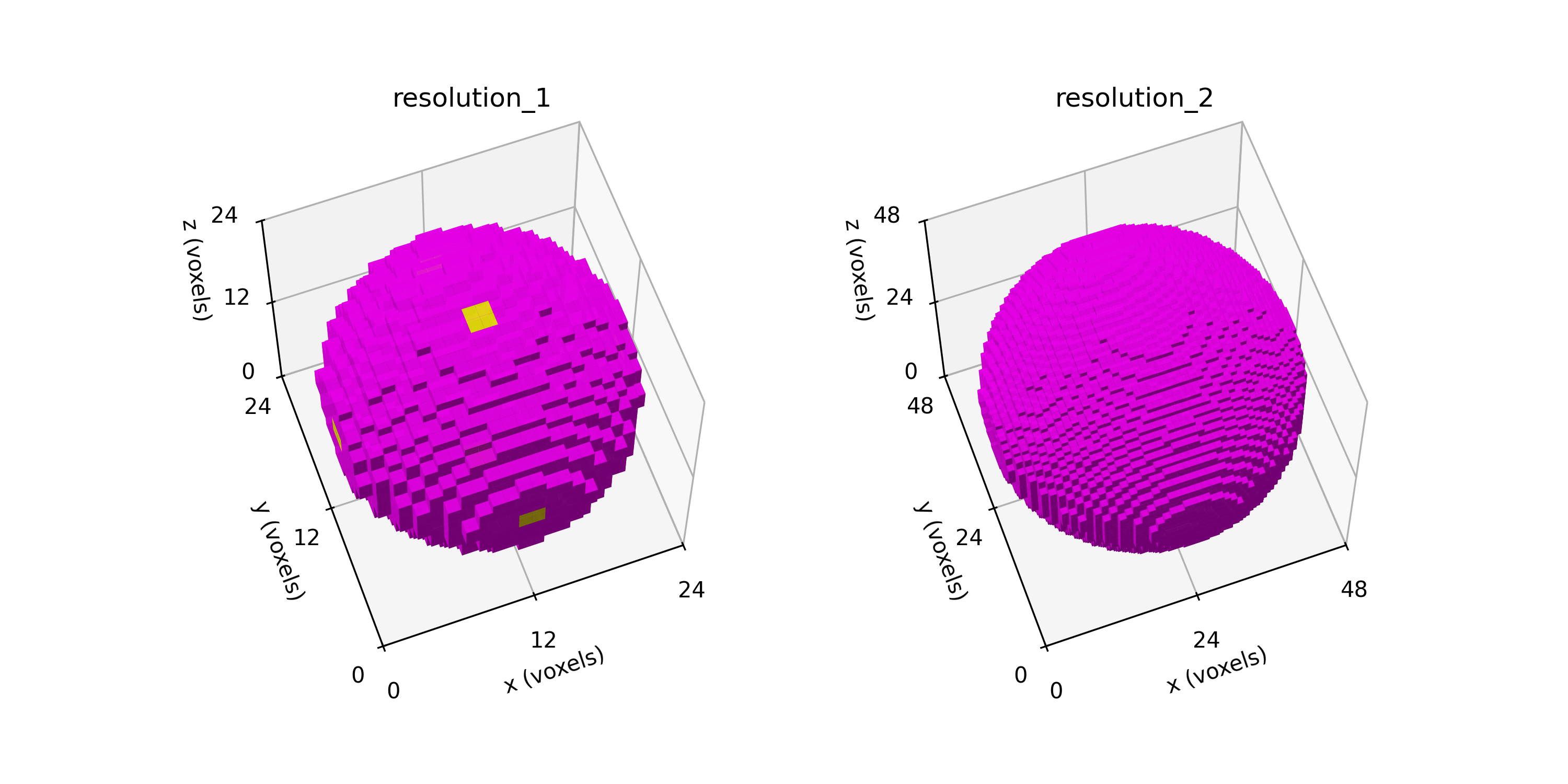
Figure: Sphere segmentations (left) spheres_resolution_1.npy and (right) spheres_resolution_2.npy shown in the voxel domain.
Because plotting large domains with Matplotlib
is slow, only the first two resolutions are shown.
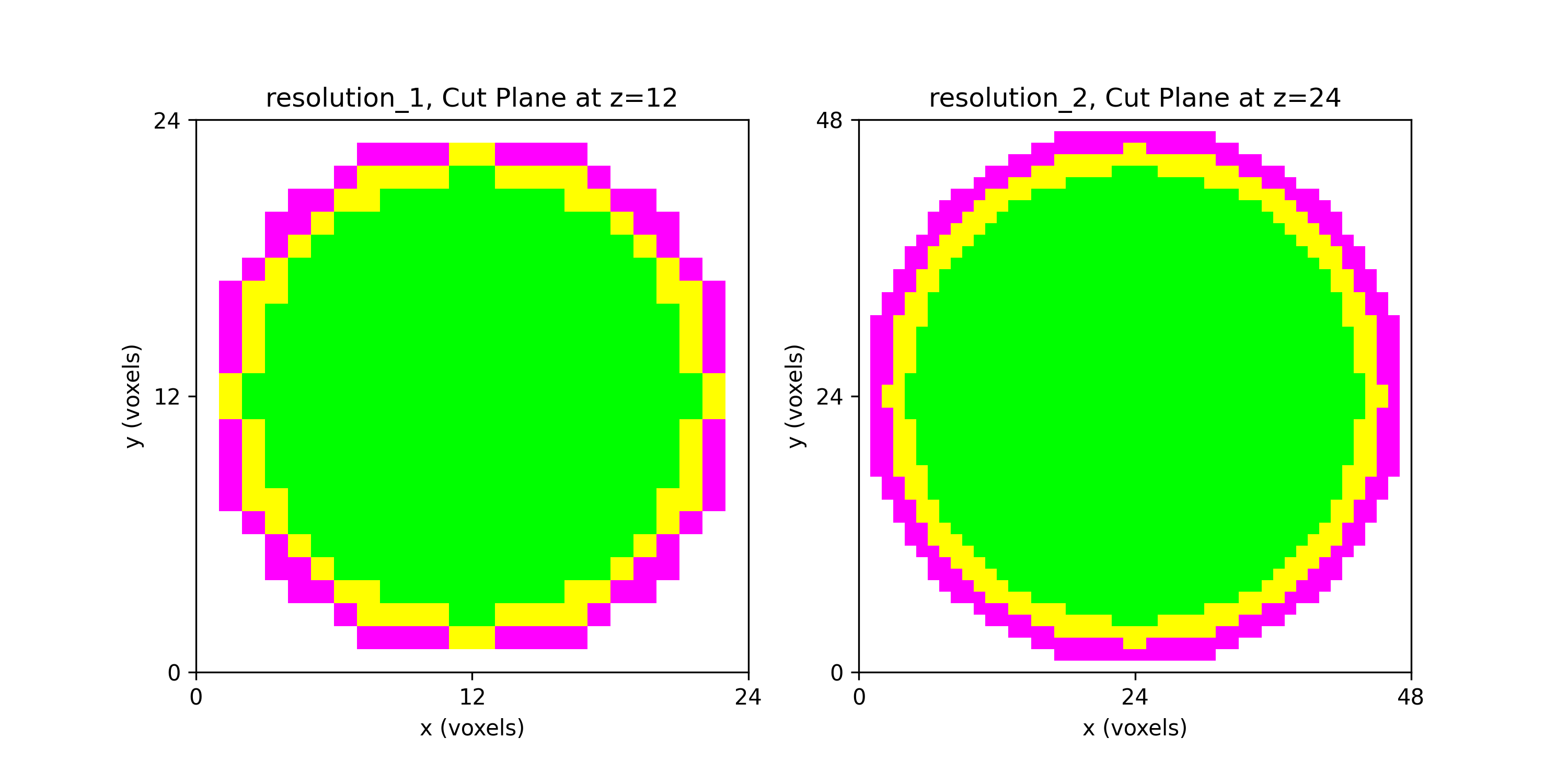
Figure: Sphere segmentations with cutting plane of (left) spheres_resolution_1.npy and (right) spheres_resolution_2.npy.
Source
spheres_cont.py