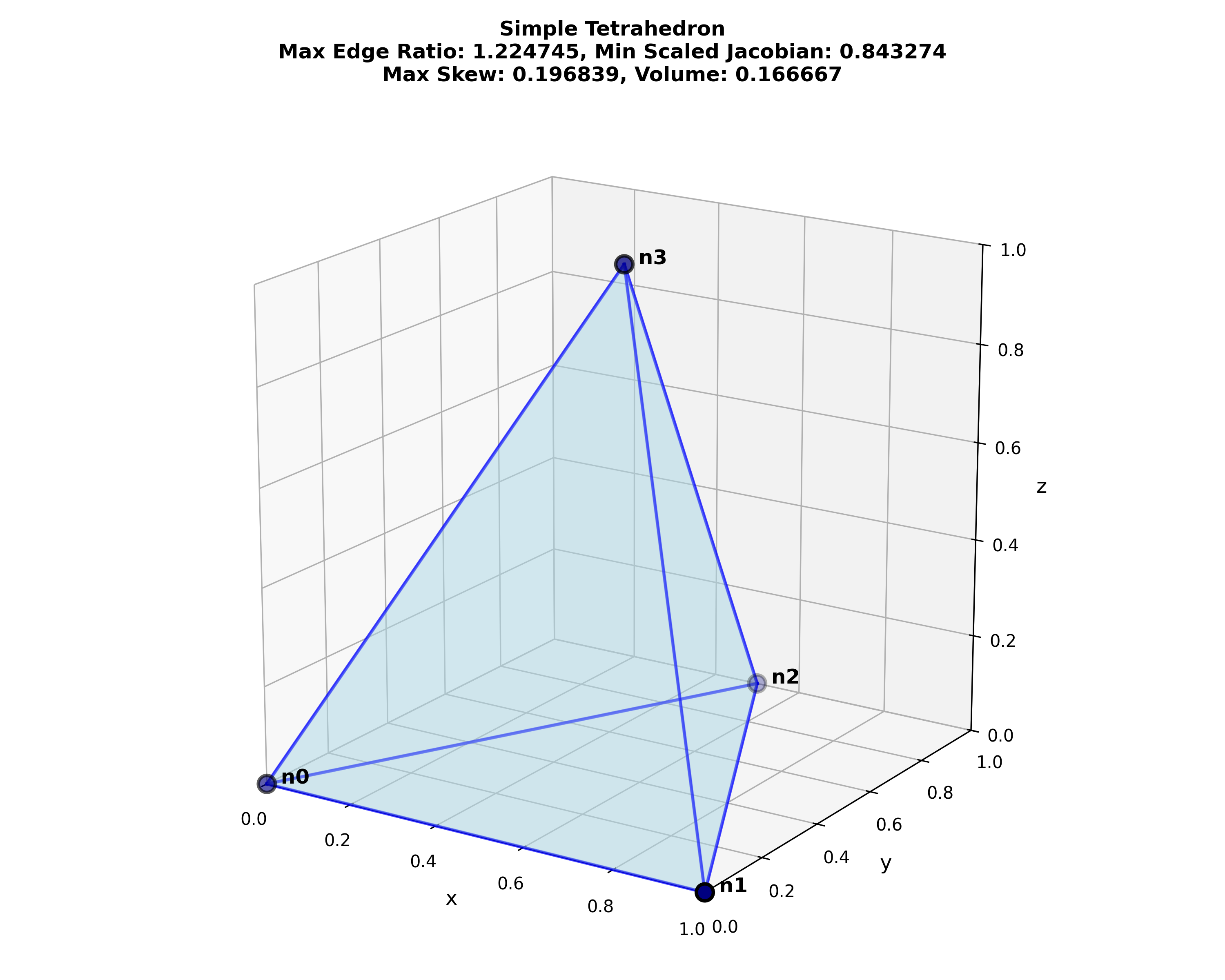
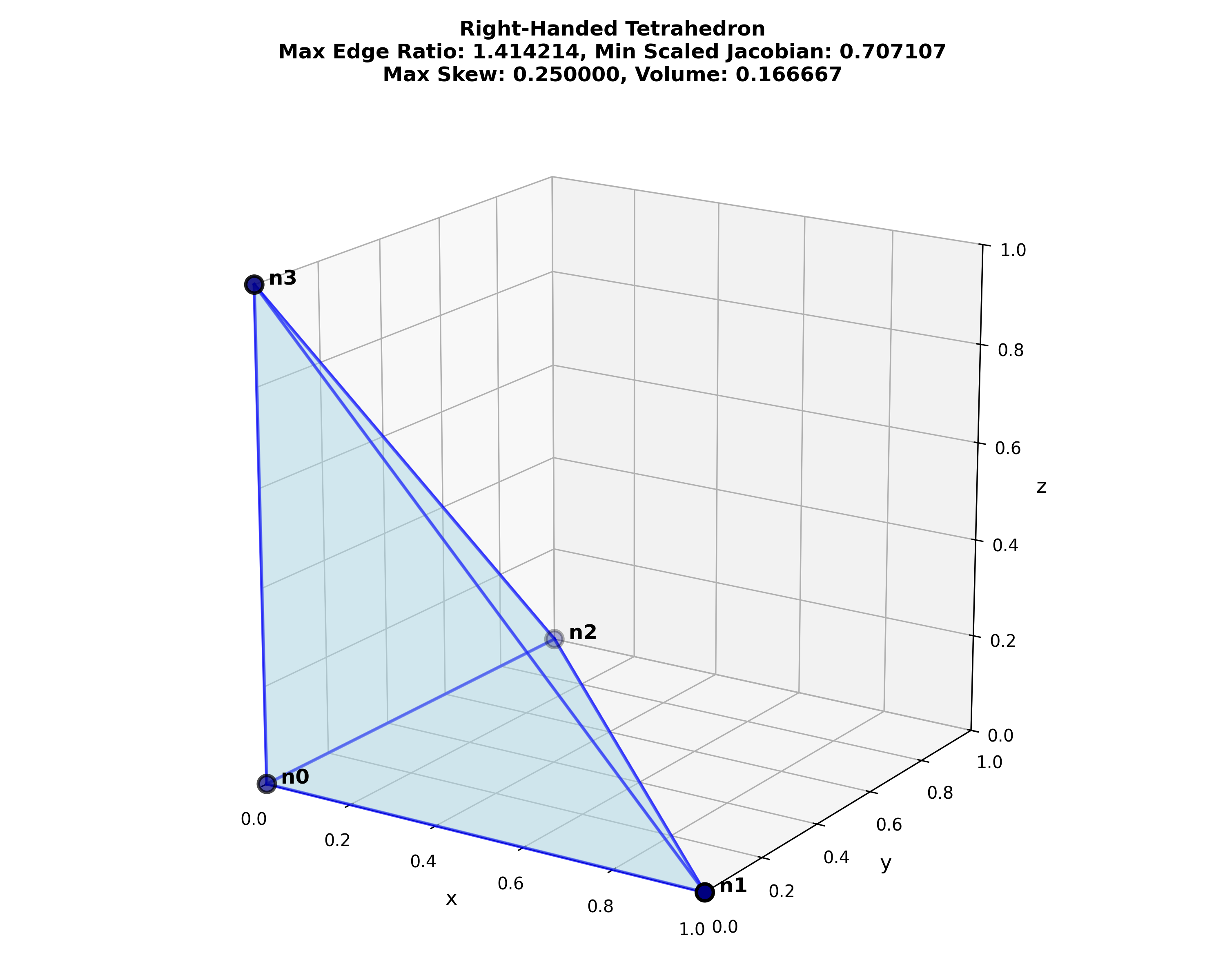
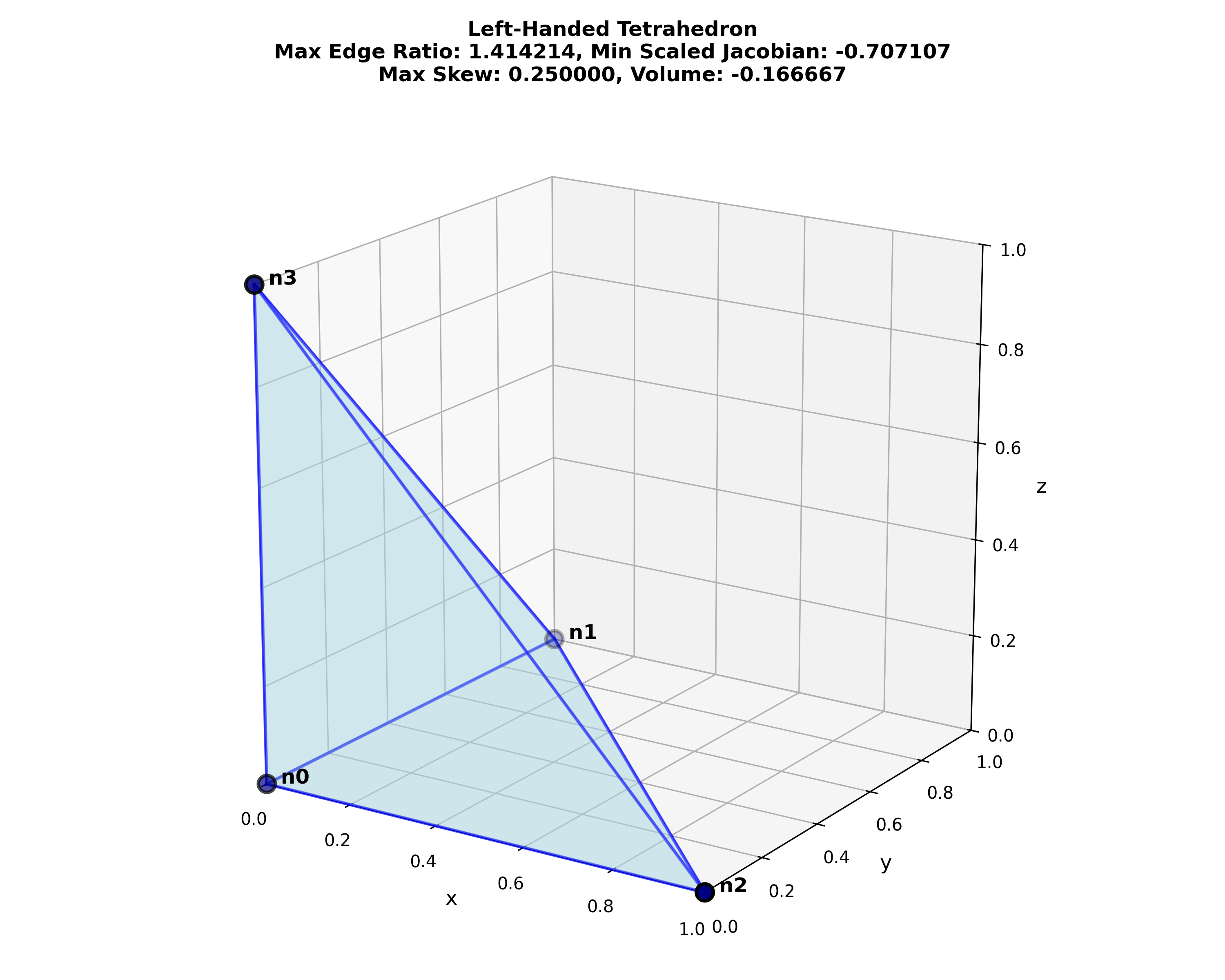
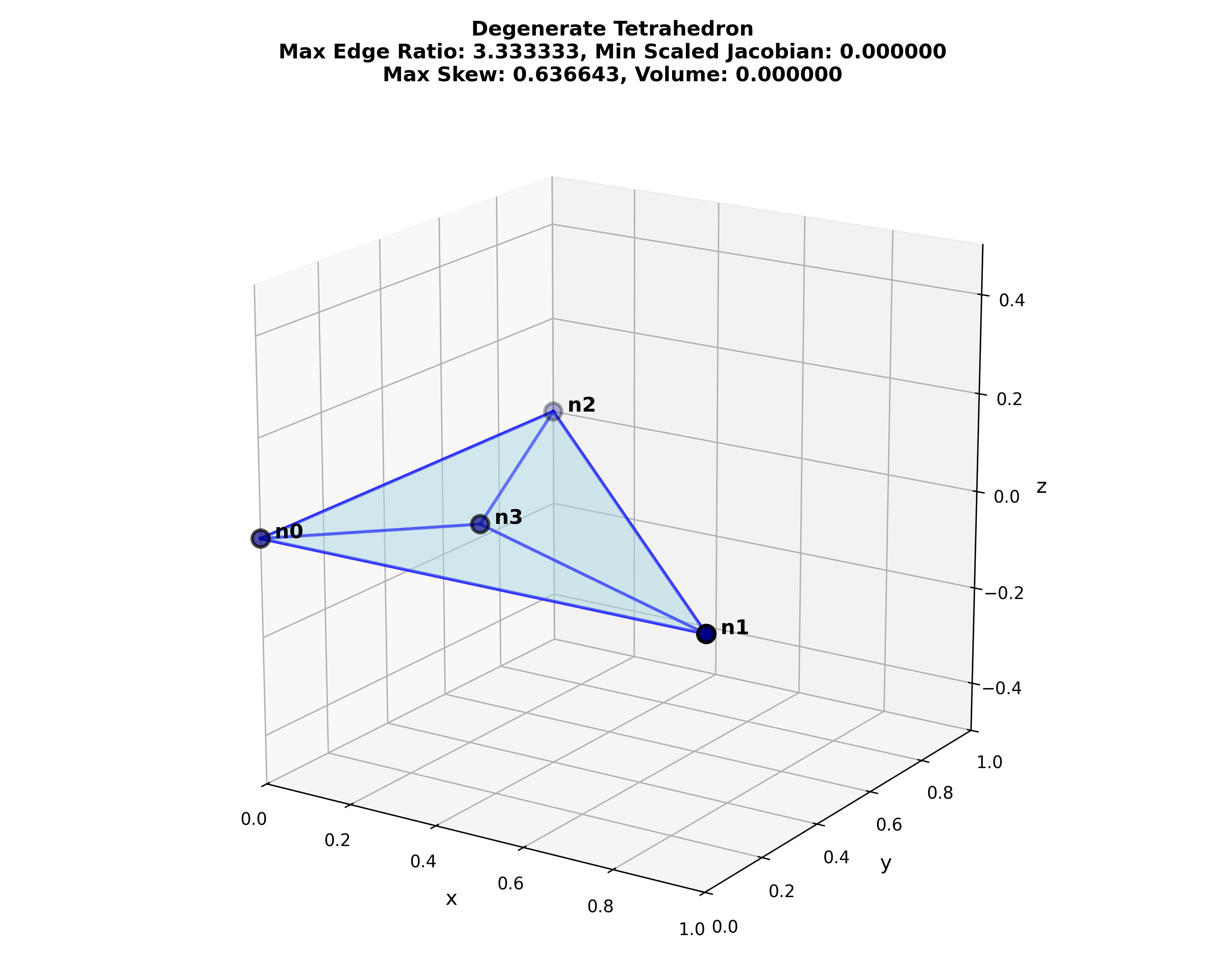
Introduction
automesh is an open-source Rust software program that uses a segmentation,
typically generated from a 3D image stack,
to create a finite element mesh,
composed either of hexahedral (volumetric)
or triangular (isosurface) elements.
automesh converts between
segmentation formats (.npy, .spn)
and
mesh formats (.exo, .inp, .mesh, .stl, .vtk).
automesh can defeature voxel domains,
apply Laplacian and Taubin smoothing,
and output mesh quality metrics.
automesh uses an internal octree for fast performance.
Segmentation
Segmentation is the process of categorizing pixels that compose a digital image into a class that represents some subject of interest. For example, in the image below, the image pixels are classified into classes of sky, trees, cat, grass, and cow.

Figure: Example of semantic segmentation, from Li et al.1
- Semantic segmentation does not differentiate between objects of the same class.
- Instance segmentation does differentiate between objects of the same class.
These two concepts are shown below:
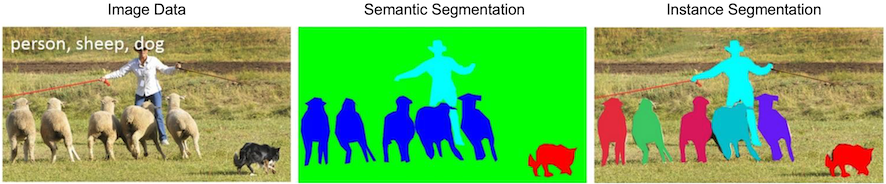
Figure: Distinction between semantic segmentation and instance segmentation, from Lin et al.2
Both segmentation types, semantic and instance, can be used with automesh. However, automesh operates on a 3D segmentation, not a 2D segmentation, as present in a digital image. To obtain a 3D segmentation, two or more images are stacked to compose a volume.
The structured volume of a stacked of pixel composes a volumetric unit called a voxel. A voxel, in the context of this work, will have the same dimensionality in the x and y dimension as the pixel in the image space, and will have the z dimensionality that is the stack interval distance between each image slice. All pixels are rectangular, and all voxels are cuboid.
The figure below illustrates the concept of stacked images:
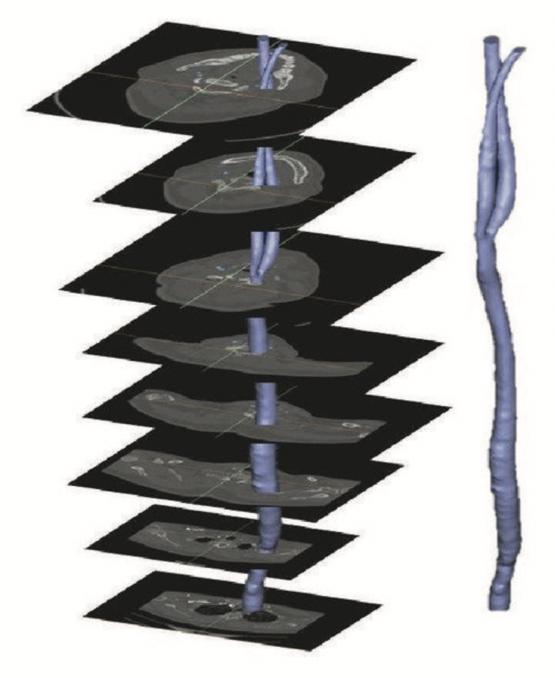
Figure: Example of stacking several images to create a 3D representation, from Bit et al.3
The digital image sources are frequently medical images, obtained by CT or MR, though automesh can be used for any subject that can be represented as a stacked segmentation. Anatomical regions are classified into categories. For example, in the image below, ten unique integers have been used to represent
bone, disc, vasculature, airway/sinus, membrane, cerebral spinal fluid, white matter, gray matter, muscle, and skin.
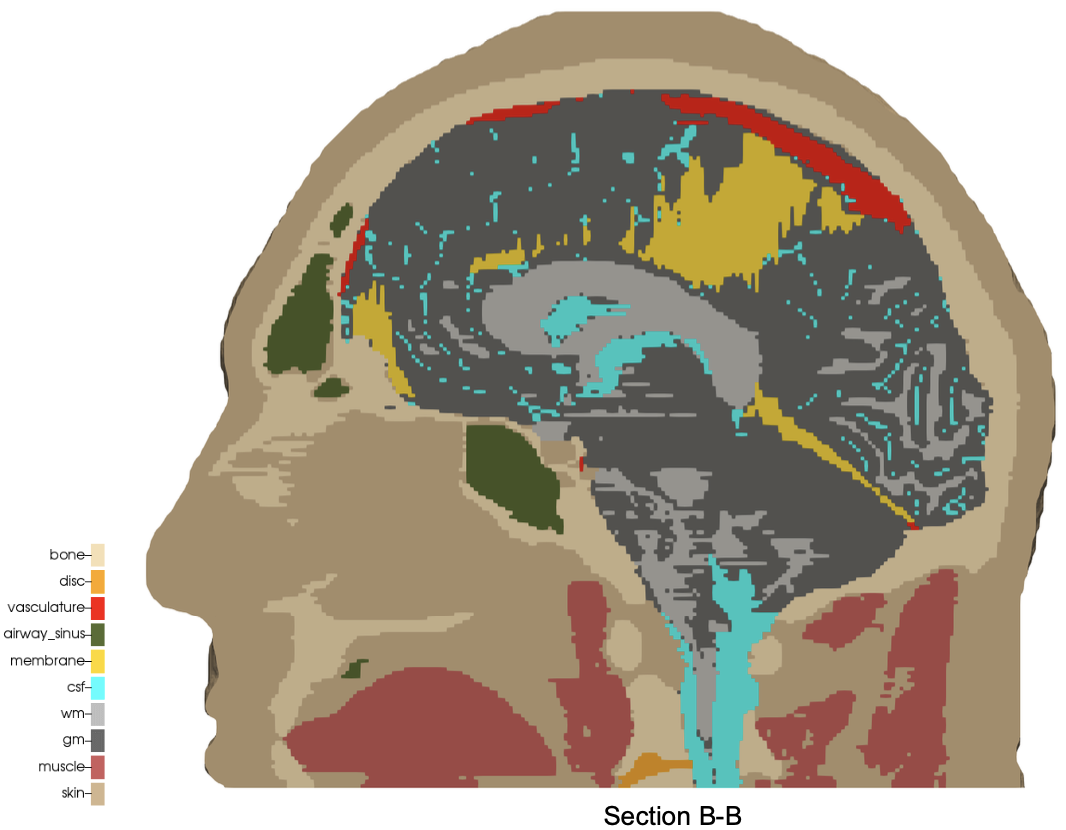
Figure: Example of a 3D voxel model, segmented into 10 categories, from Terpsma et al.4
Given a 3D segmentation, for any image slice that composes it, the pixels have been classified
into categories that are designated with unique, non-negative integers.
The range of integer values is limited to 256 = 2^8, since the uint8 data type is specified.
A practical example of a range could be [0, 1, 2, 3, 4]. The integers do not need to be sequential,
so a range of [4, 501, 2, 0, 42] is also valid, but not conventional.
Segmentations are frequently serialized (saved to disc) as either a NumPy (.npy) file
or a SPN (.spn) file.
A SPN file is a text (human-readable) file that contains a single a column of non-negative integer values. Each integer value defines a unique category of a segmentation.
Axis order (for example,
x, y, then z; or, z, y, x, etc.) is not implied by the SPN structure;
so additional data, typically provided through a configuration file, is
needed to uniquely interpret the pixel tile and voxel stack order
of the data in the SPN file.
For subjects that the human anatomy, we use the Patient Coordinate System (PCS), which directs the
x, y, and z axes to the left, posterior, and superior, as shown below:
| Patient Coordinate System: | Left, Posterior, Superior (x, y, z) |
|---|---|
 | 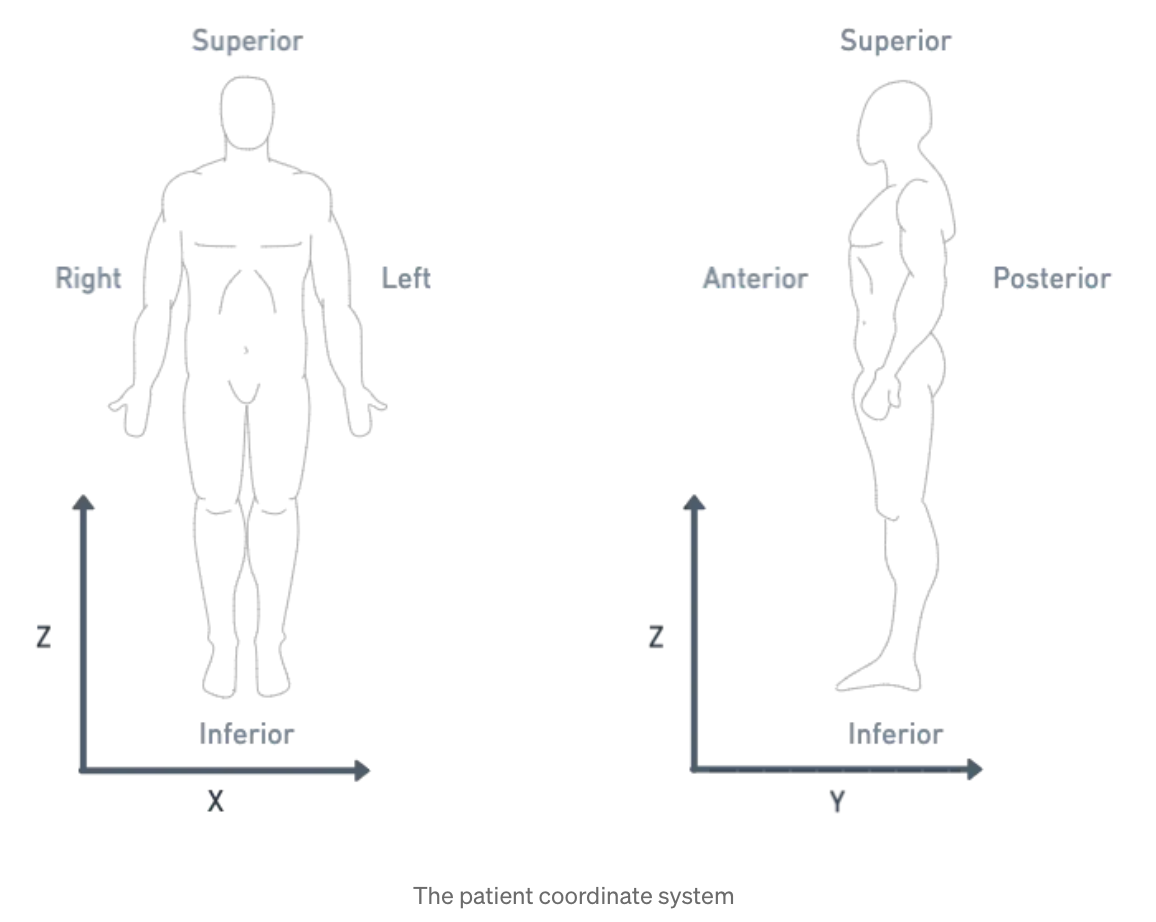 |
Figure: Illustration of the patient coordinate system, left figure from Terpsma et al.4 and right figure from Sharma.5
Finite Element Mesh
The main automesh file output type is .exo, which refers to the EXODUS II file format, or simply "Exodus" format.
Other mesh output types, such as .inp, .mesh, and .vtk, are also available.
EXODUS II is a model developed to store and retrieve data for finite element analyses. It is used for preprocesing (problem definition), postprocessing (results visualization), as well as code to code data transfer. An EXODUS II data file is a random access, machine independent binary file.6
EXODUS II depends on the Network Common Data Form (NetCDF) library.
NetCDF is a public domain database library that provides low-level data storage. The NetCDF library stores data in eXternal Data Representation (XDR) format, which provides machine independency.
EXODUS II library functions provide a map between finite element data objects and NetCDF dimensions, attributes, and variables.
EXODUS II data objects:
-
Initialization Data
- Number of nodes
- Number of elements
- optional informational text
- etc.
-
Model - static objects (i.e., objects that do not change over time)
- Nodal coordinates
- Element connectivity
- Node sets
- Side sets
-
optional Results
- Nodal results
- Element results
- Global results
Note:
automeshwill use Initialization Data and Model sections; it will not use the Results section.
We use the Exodus II convention for a hexahedral element local node numbering:
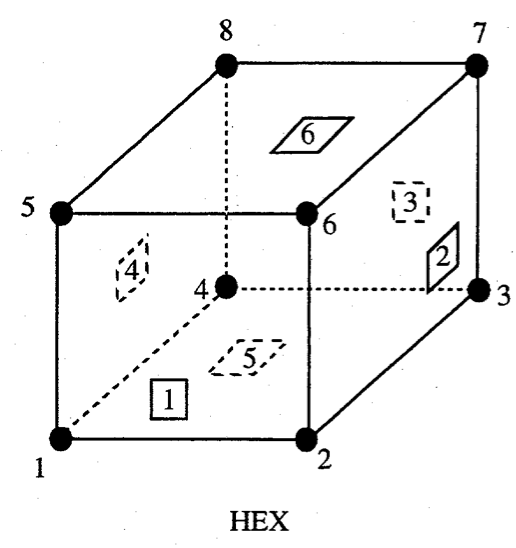
Figure: Exodus II hexahedral local finite element numbering scheme, from Schoof et al.6
References
-
Li FF, Johnson J, Yeung S. Lecture 11: Dection and Segmentation, CS 231n, Stanford Unveristy, 2017. link ↩
-
Lin TY, Maire M, Belongie S, Hays J, Perona P, Ramanan D, Dollár P, Zitnick CL. Microsoft coco: Common objects in context. In Computer Vision–ECCV 2014: 13th European Conference, Zurich, Switzerland, September 6-12, 2014, Proceedings, Part V 13 2014 (pp. 740-755). Springer International Publishing. link ↩
-
Bit A, Ghagare D, Rizvanov AA, Chattopadhyay H. Assessment of influences of stenoses in right carotid artery on left carotid artery using wall stress marker. BioMed research international. 2017;2017(1):2935195. link ↩
-
Terpsma RJ, Hovey CB. Blunt impact brain injury using cellular injury criterion. Sandia National Lab. (SNL-NM), Albuquerque, NM (United States); 2020 Oct 1. link ↩ ↩2
-
Sharma S. DICOM Coordinate Systems — 3D DICOM for computer vision engineers, Medium, 2021-12-22. link ↩
-
Schoof LA, Yarberry VR. EXODUS II: a finite element data model. Sandia National Lab. (SNL-NM), Albuquerque, NM (United States); 1994 Sep 1. link ↩ ↩2
Installation
Use automesh from one of the following interfaces:
- command line interface,
- Rust interface, or
- Python interface.
All interfaces are independent from each other:
- The Rust interfaces can be used without the Python interface.
- The Python interface can be used without the Rust interfaces.
For macOS and Linux, use a terminal. For Windows, use a Command Prompt (CMD) or PowerShell.
Some macOS users have encountered a build error with the netcdf-src crate. See Troubleshooting for a solution to this error.
Step 1: Install Prerequisites
- The command line interface and Rust interface depend on Rust and Cargo.
- Cargo is the Rust package manager.
- Cargo is included with the Rust installation.
- The Python interface depends on Python and pip.
- pip is the Python package installer.
- pip is included with the standard installation of Python starting from Python 3.4.
Rust Prerequisites
It is recommended to install Rust using Rustup, which is an installer and version management tool.
Python Prerequisites
macOS
- Install Homebrew (if you don't have it already). Open the Terminal and run:
/bin/bash -c "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/HEAD/install.sh)"
- Install Python. After Homebrew is installed, run:
brew install python
- Verify Python and pip are installed:
python3 --version
pip3 --version
Linux
- Update Package List. Open a terminal and run:
sudo apt update
- Install Python and pip. For Ubuntu or Debian-based systems, run:
sudo apt install python3 python3-pip
- Verify Python and pip are installed:
python3 --version
pip3 --version
Windows
- Download Python. Go to the official Python website and download the latest version of Python for Windows.
- Run the Installer. During installation, make sure to check the box that says "Add Python to PATH."
- Verify Python and pip are installed:
python --version
pip --version
All Environments
On all environments, a virtual environment is recommended, but not required. Create a virtual environment:
python3 -m venv .venv # venv, or
uv venv .venv # using uv
uv is a fast Python package manager, written in Rust. It is an alternative to pip.
Activate the virtual environment:
source .venv/bin/activate # for bash shell
source .venv/bin/activate.csh # for c shell
source .venv/bin/activate.fish # for fish shell
.\.venv\Scripts\activate # for powershell
Step 2: Install automesh
Install the desired interface.
Command Line Interface
cargo install automesh
Rust Interface
cargo add automesh
Python Interface
pip install automesh # using pip, or
uv pip install automesh # using uv
Step 3: Verify Installation
Rust Interfaces
Run the command line help:
automesh
which should display the following:
@@@@@@@@@@@@@@@@
@@@@ @@@@@@@@@@
@@@@ @@@@@@@@@@@ automesh: Automatic mesh generation
@@@@ @@@@@@@@@@@@
@@ @@ @@ v0.3.8 linux x86_64
@@ @@ @@ build d01ddd6 2026-02-27T16:44:12+0000
@@@@@@@@@@@@ @@@ Chad B. Hovey <chovey@sandia.gov>
@@@@@@@@@@@ @@@@ Michael R. Buche <mrbuche@sandia.gov>
@@@@@@@@@@ @@@@@ @
@@@@@@@@@@@@@@@@
Usage: automesh [COMMAND]
Commands:
convert Converts between mesh or segmentation file types
defeature Defeatures and creates a new segmentation
diff Show the difference between two segmentations
extract Extracts a specified range of voxels from a segmentation
mesh Creates a finite element mesh from a tessellation or segmentation
metrics Quality metrics for an existing finite element mesh
remesh Applies isotropic remeshing to an existing mesh
segment Creates a segmentation or voxelized mesh from an existing mesh
smooth Applies smoothing to an existing mesh
help Print this message or the help of the given subcommand(s)
Options:
-h, --help Print help
-V, --version Print version
Python Interface
python
# In Python, import the module
>>> import automesh
# List all attributes and methods of the module
>>> dir(automesh)
# Get help on the module
>>> help(automesh)
Troubleshooting
ZLIB target not found
Some users have encountered an error when trying to build the netcdf crate, e.g.,
...
error: failed to run custom build command for `netcdf-src v0.4.3`
...
The link interface of target "hdf5-static" contains:
ZLIB::ZLIB
but the target was not found. Possible reasons include:
* There is a typo in the target name.
* A find_package call is missing for an IMPORTED target.
* An ALIAS target is missing.
...
HDF5 is looking for ZLIB::ZLIB as a CMake target, but it's not being found
even though ZLIB is present.
A solution is to use a dynamically-linked netcdf from Homebrew instead of
trying to build it statically. This should avoid the CMake ZLIB::ZLIB target
issue entirely.
Update the Cargo.toml for automesh to avoid static linking:
...
# netcdf = { version = "=0.11.1", features = ["ndarray", "static"] }
netcdf = { version = "=0.11.1", features = ["ndarray"] }
...
Then,
# Make sure netcdf is installed via Homebrew
brew install netcdf
# Set the environment variable to use system netcdf
export NETCDF_DIR=/opt/homebrew
# Clean and build
cargo clean
cargo build
If you still encounter errors about netcdf not being found, also try:
export PKG_CONFIG_PATH=/opt/homebrew/lib/pkgconfig
export DYLD_LIBRARY_PATH=/opt/homebrew/lib
Getting Started
In this section, we use a simple segmentation to create a finite element mesh, a smoothed finite element mesh, and an isosurface.
Segmentation Input
We start with a segmentation of a regular octahedron composed of three materials. The segmentation encodes
0for void (or background), shown in gray,1for the inner domain, shown in green,2for the intermediate layer, shown in yellow, and3for the outer layer, shown in magenta.
The (7 x 7 x 7) segmentation, at the midline cut plane,
appears as follows:
Consider each slice, 1 to 7, in succession:
Remark: The (
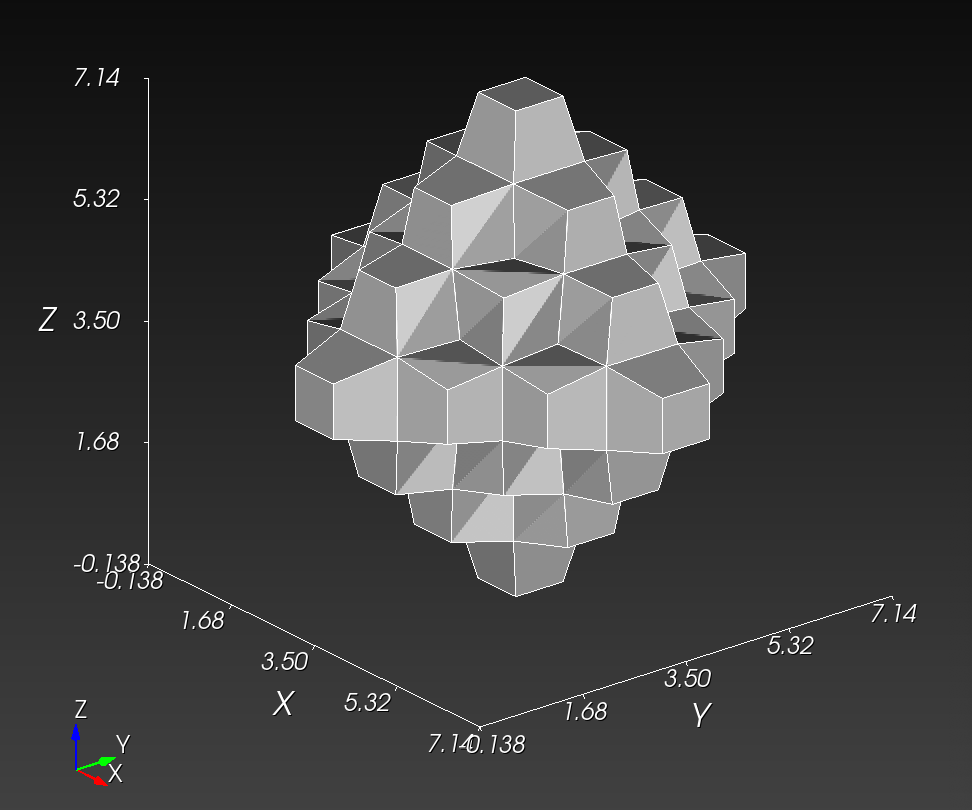
7 x 7 x 7) segmentation can be thought of as a conceptual start point for a process called Loop subdivision, used to produce spherical shapes at higher resolutions. See Octa Loop for additional information. A sphere in resolutions of (24 x 24 x 24) and (48 x 48 x 48), used in the Sphere with Shells section, is shown below:
Segmentation File Types
Two types of segmentation files types are supported: .spn and .npy.
The .spn file can be thought of as the most elementary segmentation file type because it is
saved as an ASCII text file and is therefore readily human-readable.
Below is an abbreviated and commented .spn segmentation of the (7 x 7 x 7) octahedron
discussed above.
0 # slice 1, row 1
0
0
0
0
0
0
0 # slice 1, row 2
0
0
0
0
0
0
0 # slice 1, row 3
0
0
0
0
0
0
0 # slice 1, row 4
0
0
3
0
0
0
0 # slice 1, row 5
0
0
0
0
0
0
0 # slice 1, row 6
0
0
0
0
0
0
0 # slice 1, row 7
0
0
0
0
0
0
# ... and so on for the remaining six slices
A disadvantage of .spn is that it can become difficult to keep track of data
slice-by-slice. Because it is not a compressed binary file, the .spn has a
larger file size than the equivalent .npy.
The .npy segmentation file format is an alternative to the .spn
format. The .npy format can be advantageous because is can be generated easily
from Python. This approach can be useful because Python can be used to
algorithmically create a segmentation and serialized the segmentation to a compressed
binary file in .npy format.
We illustrate creating the octahedron segmentation in Python:
"""This module creates a 7x7x7 octahedron segmentation."""
import numpy as np
segmentation = np.array(
[
[ # slice 1
[0, 0, 0, 0, 0, 0, 0], # row 1
[0, 0, 0, 0, 0, 0, 0], # row 2
[0, 0, 0, 0, 0, 0, 0], # row 3
[0, 0, 0, 3, 0, 0, 0], # row 4
[0, 0, 0, 0, 0, 0, 0], # row 5
[0, 0, 0, 0, 0, 0, 0], # row 6
[0, 0, 0, 0, 0, 0, 0], # row 7
],
[ # slice 2
[0, 0, 0, 0, 0, 0, 0], # row 1
[0, 0, 0, 0, 0, 0, 0], # row 2
[0, 0, 0, 3, 0, 0, 0], # row 3
[0, 0, 3, 2, 3, 0, 0], # row 4
[0, 0, 0, 3, 0, 0, 0], # row 5
[0, 0, 0, 0, 0, 0, 0], # row 6
[0, 0, 0, 0, 0, 0, 0], # row 7
],
[ # slice 3
[0, 0, 0, 0, 0, 0, 0], # row 1
[0, 0, 0, 3, 0, 0, 0], # row 2
[0, 0, 3, 2, 3, 0, 0], # row 3
[0, 3, 2, 1, 2, 3, 0], # row 4
[0, 0, 3, 2, 3, 0, 0], # row 5
[0, 0, 0, 3, 0, 0, 0], # row 6
[0, 0, 0, 0, 0, 0, 0], # row 7
],
[ # slice 4
[0, 0, 0, 3, 0, 0, 0], # row 1
[0, 0, 3, 2, 3, 0, 0], # row 2
[0, 3, 2, 1, 2, 3, 0], # row 3
[3, 2, 1, 1, 1, 2, 3], # row 4
[0, 3, 2, 1, 2, 3, 0], # row 5
[0, 0, 3, 2, 3, 0, 0], # row 6
[0, 0, 0, 3, 0, 0, 0], # row 7
],
[ # slice 5
[0, 0, 0, 0, 0, 0, 0], # row 1
[0, 0, 0, 3, 0, 0, 0], # row 2
[0, 0, 3, 2, 3, 0, 0], # row 3
[0, 3, 2, 1, 2, 3, 0], # row 4
[0, 0, 3, 2, 3, 0, 0], # row 5
[0, 0, 0, 3, 0, 0, 0], # row 6
[0, 0, 0, 0, 0, 0, 0], # row 7
],
[ # slice 6
[0, 0, 0, 0, 0, 0, 0], # row 1
[0, 0, 0, 0, 0, 0, 0], # row 2
[0, 0, 0, 3, 0, 0, 0], # row 3
[0, 0, 3, 2, 3, 0, 0], # row 4
[0, 0, 0, 3, 0, 0, 0], # row 5
[0, 0, 0, 0, 0, 0, 0], # row 6
[0, 0, 0, 0, 0, 0, 0], # row 7
],
[ # slice 7
[0, 0, 0, 0, 0, 0, 0], # row 1
[0, 0, 0, 0, 0, 0, 0], # row 2
[0, 0, 0, 0, 0, 0, 0], # row 3
[0, 0, 0, 3, 0, 0, 0], # row 4
[0, 0, 0, 0, 0, 0, 0], # row 5
[0, 0, 0, 0, 0, 0, 0], # row 6
[0, 0, 0, 0, 0, 0, 0], # row 7
],
],
dtype=np.uint8,
)
FILE_NAME = "octahedron.npy"
np.save(FILE_NAME, segmentation)
print(f"Saved {FILE_NAME} with shape {segmentation.shape}.")
The convert Command
automesh allows for interoperability between .spn. and .npy file types.
Use the automesh help to discover the command syntax:
automesh convert --help
Converts between mesh or segmentation file types
Usage: automesh convert <COMMAND>
Commands:
mesh Converts mesh file types (exo | inp | stl) -> (exo | mesh | stl | vtk)
segmentation Converts segmentation file types (npy | spn) -> (npy | spn)
help Print this message or the help of the given subcommand(s)
Options:
-h, --help Print help
For example, to convert the octahedron.npy to octahedron2.spn:
automesh convert segmentation -i octahedron.npy -o octahedron2.spn
automesh 0.3.8
Reading octahedron.npy
Done 75.845µs [4 materials, 343 voxels]
Writing octahedron2.spn
Done 45.431µs
Total 446.1µs
To convert from octahedron2.spn to octahedron3.npy:
automesh convert segmentation -i octahedron2.spn -x 7 -y 7 -z 7 -o octahedron3.npy
automesh 0.3.8
Reading octahedron2.spn
Done 36.585µs [4 materials, 343 voxels]
Writing octahedron3.npy
Done 32.926µs
Total 345.014µs
Remark: Notice that the
.spnrequires number of voxels in each of the x, y, and z dimensions to be specified using--nelx,--nely,--nelz(or, equivalently-x,-y,-z) flags.
We can verify the two .npy files encode the same segmentation:
"""The purpose of this module is to show that the
segmentation data encoded in two .npy files is the same.
"""
import numpy as np
aa = np.load("octahedron.npy")
print(aa)
bb = np.load("octahedron3.npy")
print(bb)
comparison = aa == bb
print(comparison)
result = np.all(comparison)
print(f"Element-by-element equality is {result}.")
Mesh Generation
automesh creates several finite element mesh file types from
a segmentation.
Use the automesh help to discover the command syntax:
automesh mesh --help
Creates a finite element mesh from a tessellation or segmentation
Usage: automesh mesh <COMMAND>
Commands:
hex Creates an all-hexahedral mesh from a tessellation or segmentation
tet Creates an all-tetrahedral mesh from a tessellation or segmentation
tri Creates all-triangular isosurface(s) from a tessellation or segmentation
help Print this message or the help of the given subcommand(s)
Options:
-h, --help Print help
To convert the octahedron.npy into an ABAQUS finite element mesh, while removing
segmentation 0 from the mesh:
automesh mesh hex -r 0 -i octahedron.npy -o octahedron.inp
automesh 0.3.8
Reading octahedron.npy
Done 62.609µs [4 materials, 343 voxels]
Meshing voxels into hexahedra
Done 272.245µs [3 blocks, 63 elements, 160 nodes]
Writing octahedron.inp
Done 194.175µs
Total 842.835µs
Smoothing
Use the automesh help to discover the command syntax:
automesh smooth --help
Applies smoothing to an existing mesh
Usage: automesh smooth <COMMAND>
Commands:
hex Smooths an all-hexahedral mesh
tet Smooths an all-tetrahedral mesh
tri Smooths an all-triangular mesh
help Print this message or the help of the given subcommand(s)
Options:
-h, --help Print help
To smooth the octahedron.inp mesh with Taubin smoothing parameters for five
iterations:
automesh smooth hex -n 5 -i octahedron.inp -o octahedron_s05.inp
automesh 0.3.8
Reading octahedron.inp
Done 133.775µs
Smoothing with 5 iterations of Taubin
Done 63.685µs
Writing octahedron_s05.inp
Done 153.503µs
Total 631.939µs
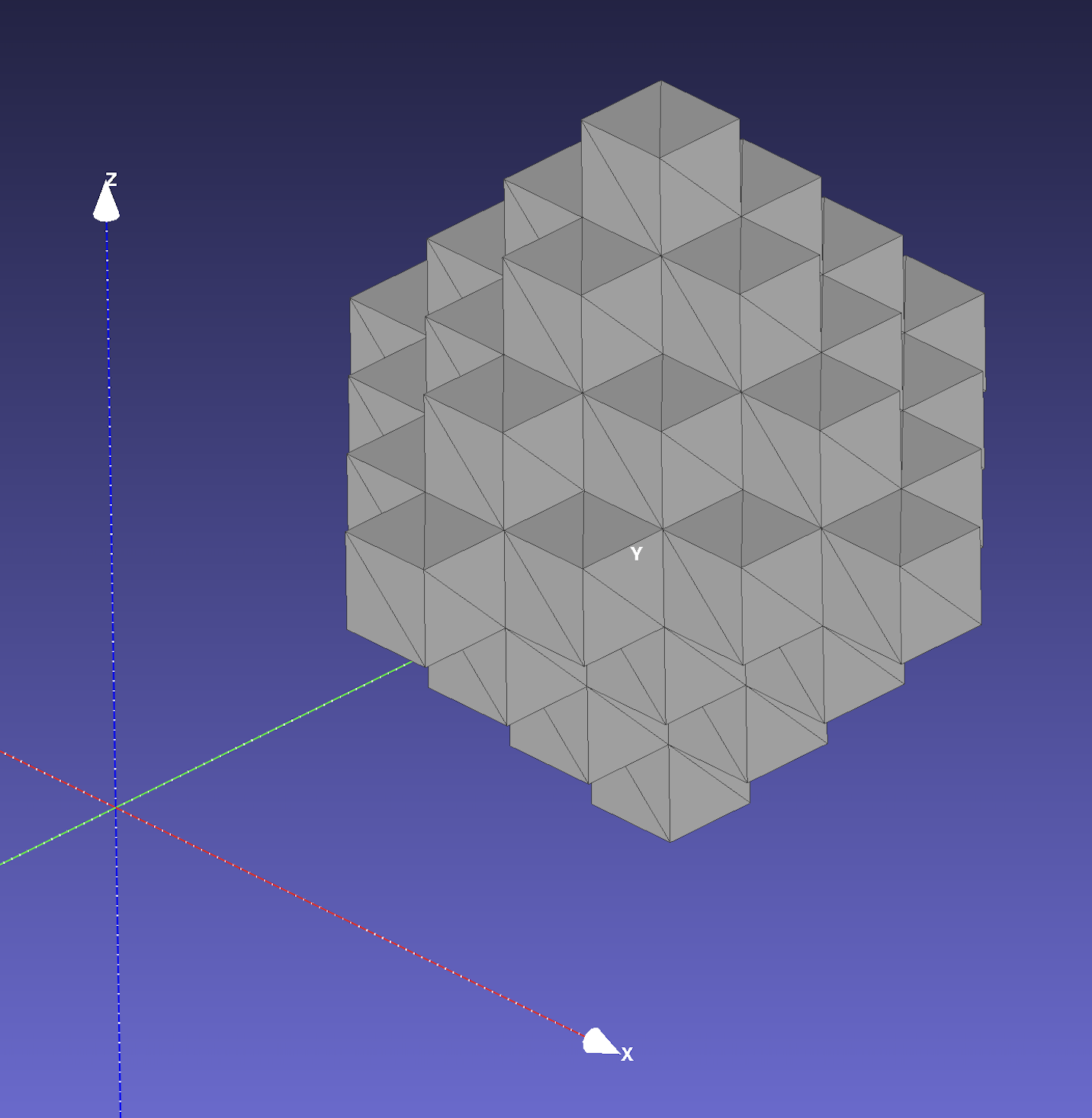
The original voxel mesh and the smoothed voxel mesh are shown below:
octahedron.inp | octahedron_s05.inp |
|---|---|
 |  |
See the Smoothing section for more information.
Isosurface
An isosurface can be generated from a segmentation using the tri command.
To create a mesh of the outer isosurfaces contained in the octahedron example:
automesh mesh tri -r 0 1 2 -i octahedron.npy -o octahedron.stl
automesh 0.3.8
Reading octahedron.npy
Done 62.328µs [4 materials, 343 voxels]
Meshing internal surfaces
Done 557.514µs [38 blocks, 456 elements, 808 nodes]
Writing octahedron.stl
Done 70.314µs
Total 985.194µs
The surfaces are visualized below:
octahedron.stl in MeshLab | octahedron.stl in Cubit with cut plane |
|---|---|
 |  |
automesh creates an isosurface from the boundary faces of voxels. The
quadrilateral faces are divided into two triangles. The Isosurface section contains more details about alternative methods used to create an isosurface.
The Sphere with Shells section contains more examples of the command line interface.
Examples
Following are examples created with automesh.
Unit Tests
The following illustates a subset of the unit tests used to validate the code implementation. For a complete listing of the unit sets, see voxels.rs and voxel.py.
The Python code used to generate the figures is included below.
Remark: We use the convention np when importing numpy as follows:
import numpy as np
Single
The minimum working example (MWE) is a single voxel, used to create a single mesh consisting of one block consisting of a single element. The NumPy input single.npy contains the following segmentation:
segmentation = np.array(
[
[
[ 11, ],
],
],
dtype=np.uint8,
)
where the segmentation 11 denotes block 11 in the finite element mesh.
Remark: Serialization (write and read)
| Write | Read |
|---|---|
Use the np.save command to serialize the segmentation a .npy file | Use the np.load command to deserialize the segmentation from a .npy file |
Example: Write the data in segmentation to a file called seg.npynp.save("seg.npy", segmentation) | Example: Read the data from the file seg.npy to a variable called loaded_arrayloaded_array = np.load("seg.npy") |
Equivalently, the single.spn contains a single integer:
11 # x:1 y:1 z:1
The resulting finite element mesh is visualized is shown in the following figure:
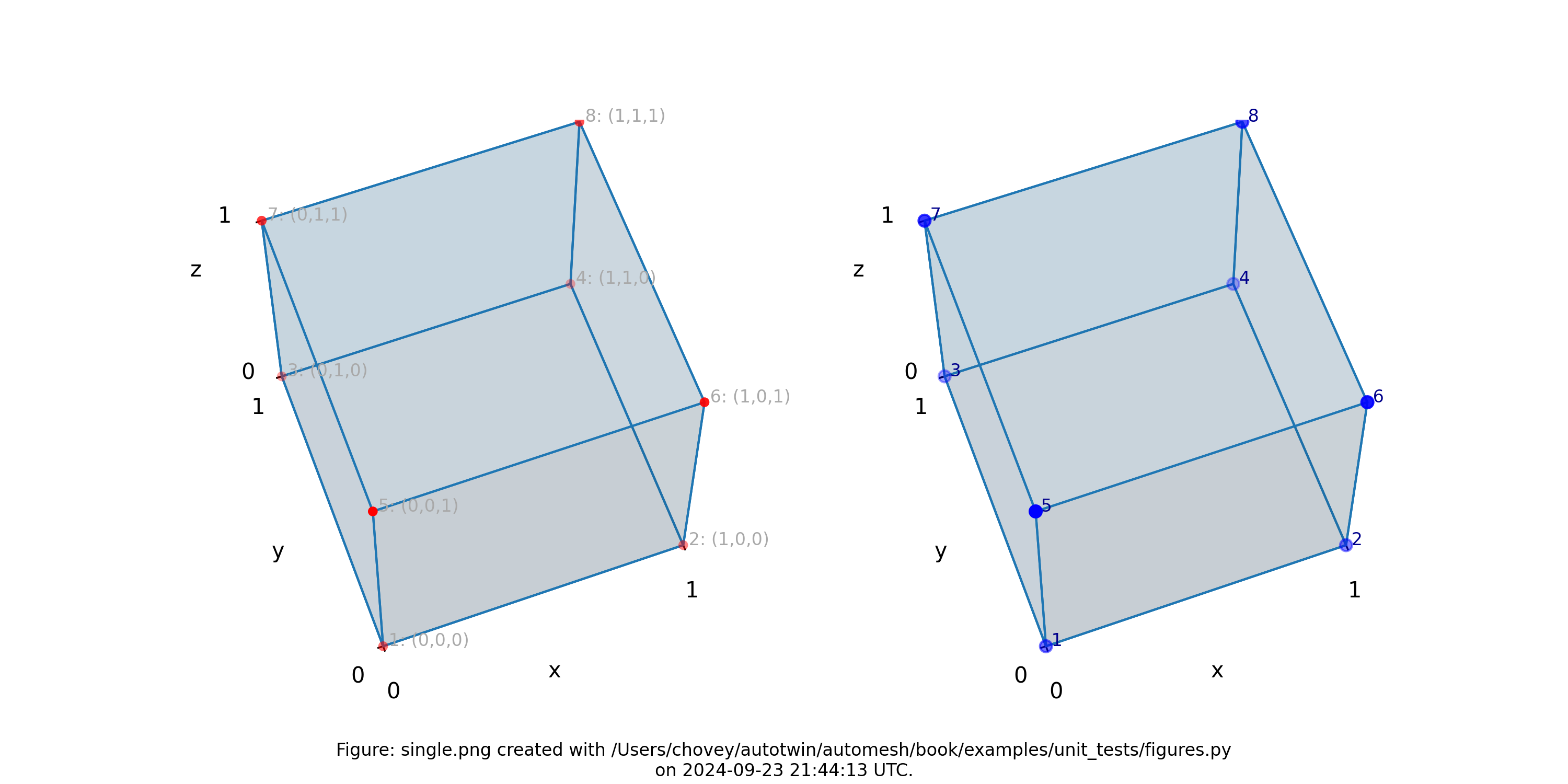
Figure: The single.png visualization, (left) lattice node numbers, (right)
mesh node numbers. Lattice node numbers appear in gray, with (x, y, z)
indices in parenthesis. The right-hand rule is used. Lattice coordinates
start at (0, 0, 0), and proceed along the x-axis, then
the y-axis, and then the z-axis.
The finite element mesh local node numbering map to the following global node numbers identically, and :
[1, 2, 4, 3, 5, 6, 8, 7]
->
[1, 2, 4, 3, 5, 6, 8, 7]
which is a special case not typically observed, as shown in more complex examples below.
Remark: Input .npy and .spn files for the examples below can be found on the repository at automesh/tests/input.
Double
The next level of complexity example is a two-voxel domain, used to create
a single block composed of two finite elements. We test propagation in
both the x and y directions. The figures below show these two
meshes.
Double X
11 # x:1 y:1 z:1
11 # 2 1 1
where the segmentation 11 denotes block 11 in the finite element mesh.
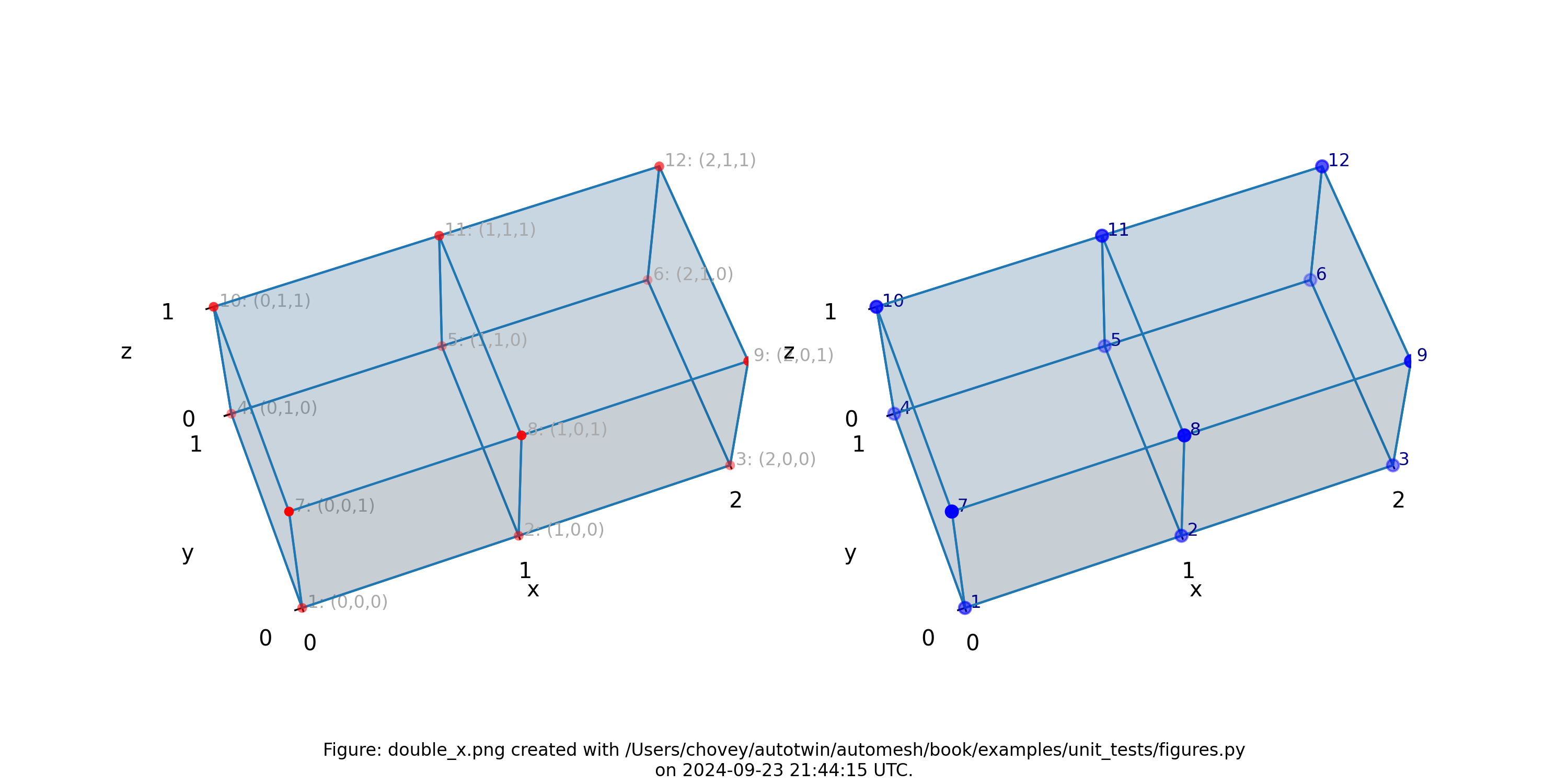
Figure: Mesh composed of a single block with two elements, propagating along
the x-axis, (left) lattice node numbers, (right) mesh node numbers.
Double Y
11 # x:1 y:1 z:1
11 # 1 2 1
where the segmentation 11 denotes block 11 in the finite element mesh.
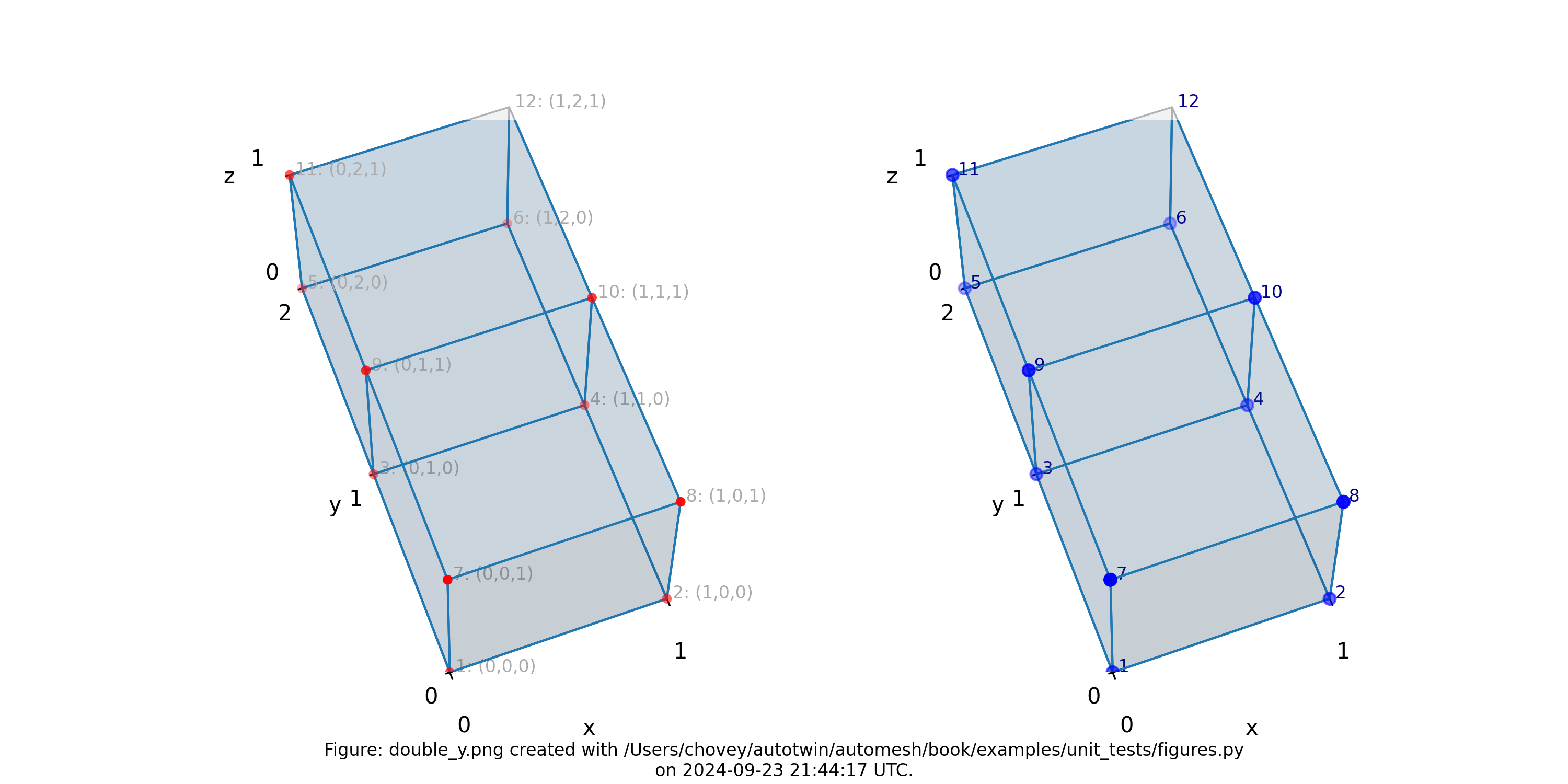
Figure: Mesh composed of a single block with two elements, propagating along
the y-axis, (left) lattice node numbers, (right) mesh node numbers.
Triple
11 # x:1 y:1 z:1
11 # 2 1 1
11 # 3 1 1
where the segmentation 11 denotes block 11 in the finite element mesh.
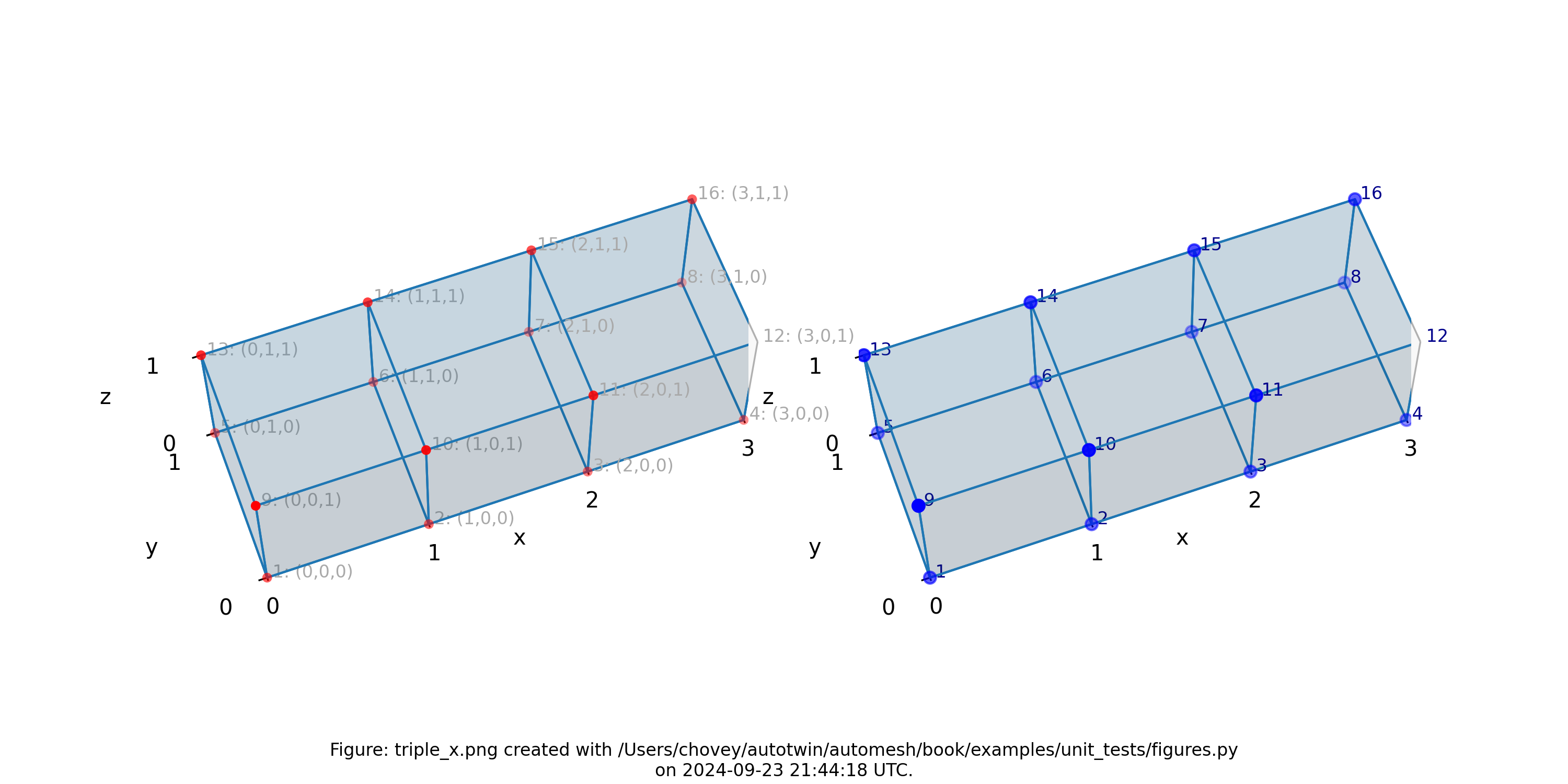
Figure: Mesh composed of a single block with three elements, propagating along
the x-axis, (left) lattice node numbers, (right) mesh node numbers.
Quadruple
11 # x:1 y:1 z:1
11 # 2 1 1
11 # 3 1 1
11 # 4 1 1
where the segmentation 11 denotes block 11 in the finite element mesh.
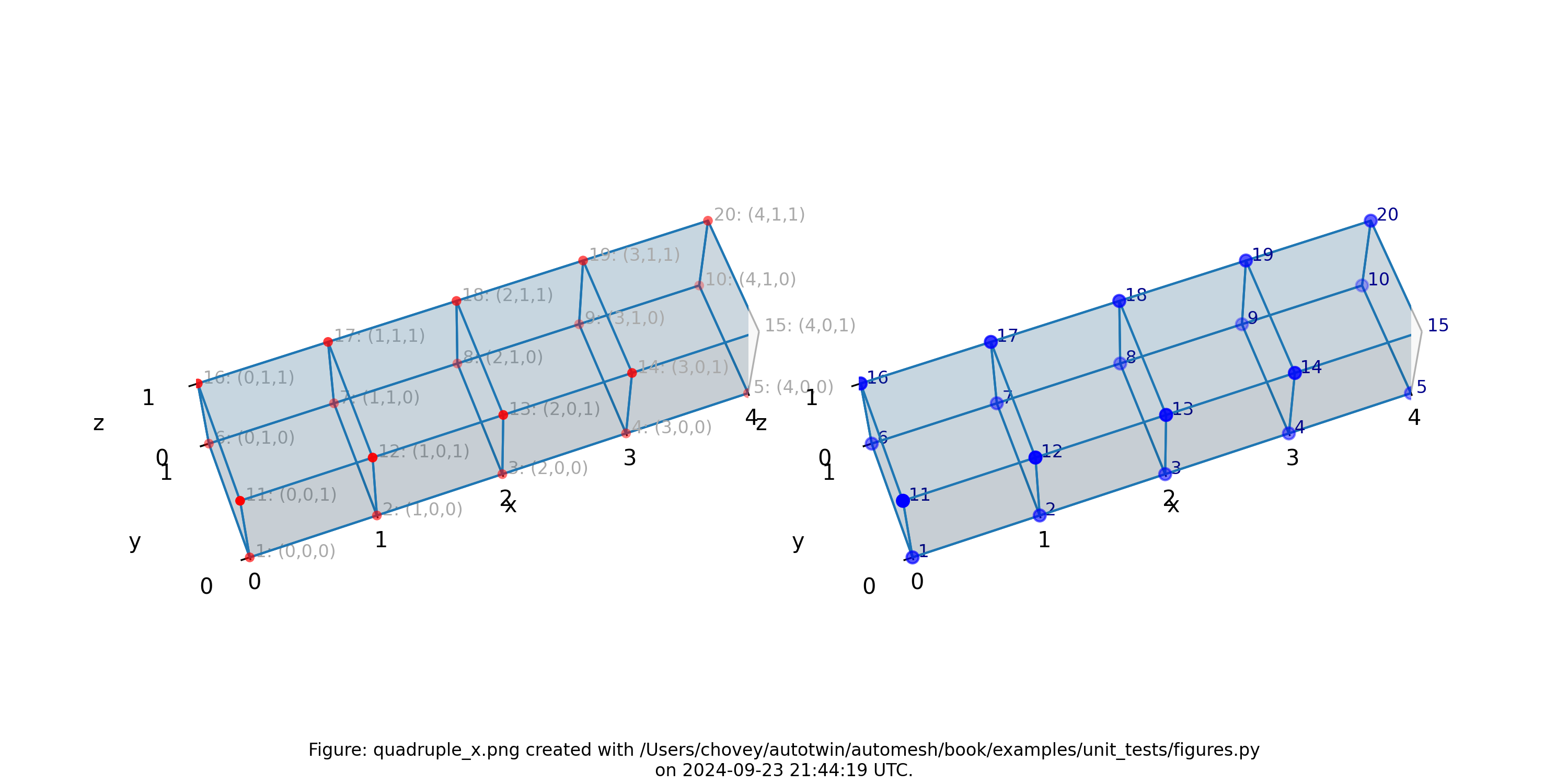
Figure: Mesh composed of a single block with four elements, propagating along
the x-axis, (left) lattice node numbers, (right) mesh node numbers.
Quadruple with Voids
99 # x:1 y:1 z:1
0 # 2 1 1
0 # 3 1 1
99 # 4 1 1
where the segmentation 99 denotes block 99 in the finite element mesh, and segmentation 0 is excluded from the mesh.
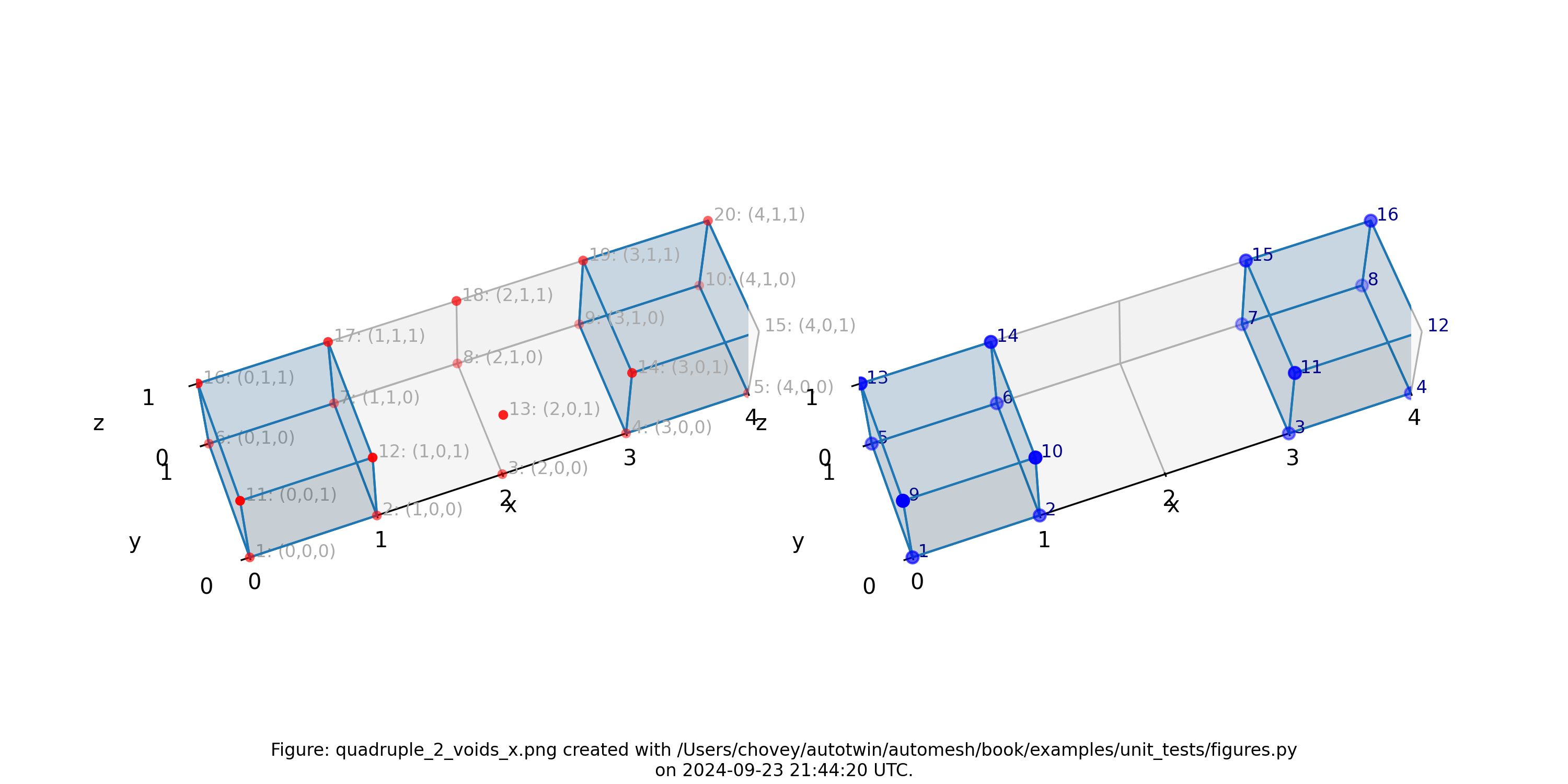
Figure: Mesh composed of a single block with two elements, propagating along
the x-axis and two voids, (left) lattice node numbers, (right) mesh node
numbers.
Quadruple with Two Blocks
100 # x:1 y:1 z:1
101 # 2 1 1
101 # 3 1 1
100 # 4 1 1
where the segmentation 100 and 101 denotes block 100 and 101,
respectively in the finite element mesh.
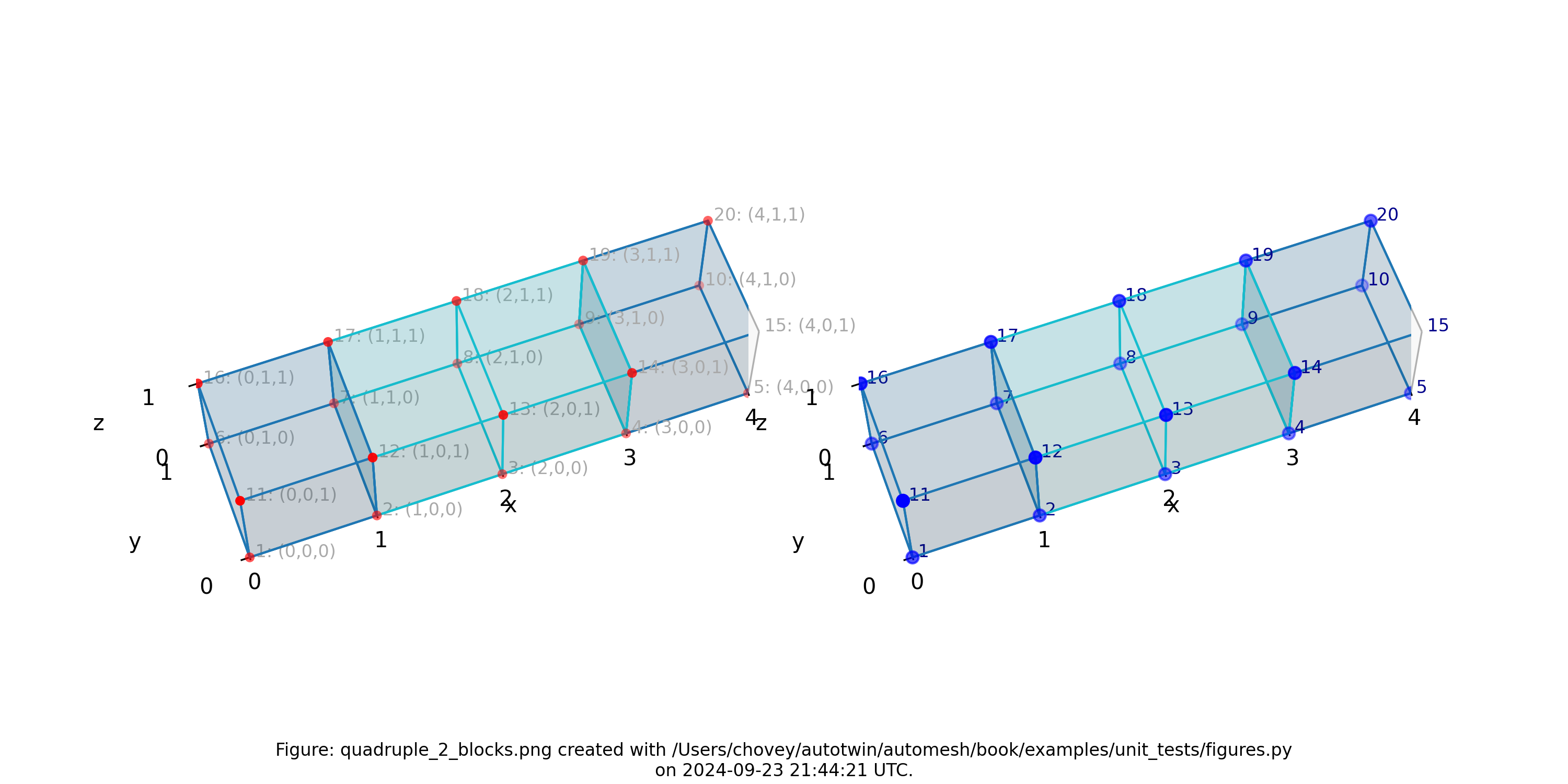
Figure: Mesh composed of two blocks with two elements elements each,
propagating along the x-axis, (left) lattice node numbers, (right) mesh
node numbers.
Quadruple with Two Blocks and Void
102 # x:1 y:1 z:1
103 # 2 1 1
0 # 3 1 1
102 # 4 1 1
where the segmentation 102 and 103 denotes block 102 and 103,
respectively, in the finite element mesh, and segmentation 0 will be included from the finite element mesh.
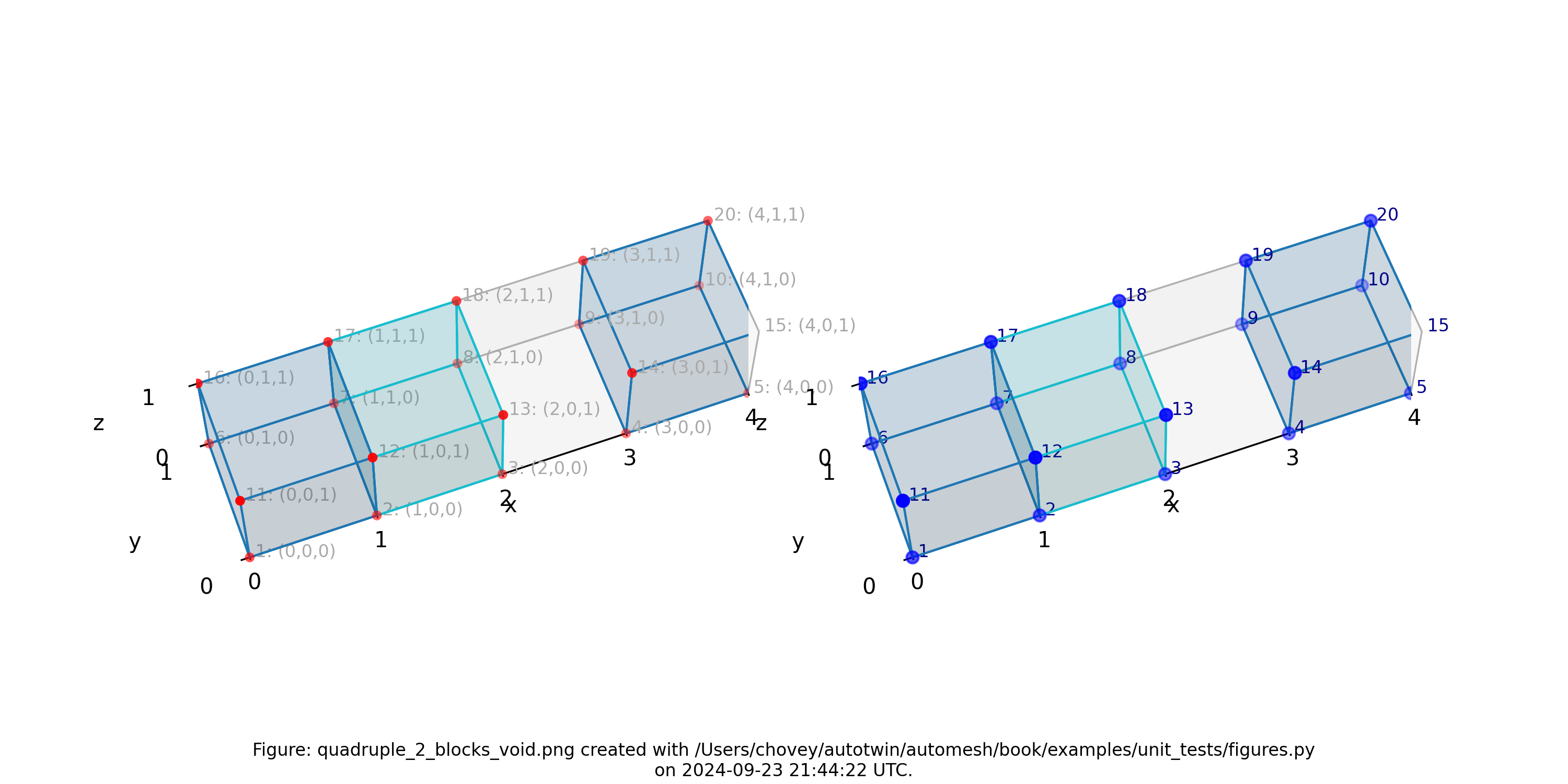
Figure: Mesh composed of one block with two elements, a second block with one
element, and a void, propagating along the x-axis, (left) lattice node
numbers, (right) mesh node numbers.
Cube
11 # x:1 y:1 z:1
11 # _ 2 _ 1 1
11 # 1 2 1
11 # _ 2 _ 2 _ 1
11 # 1 1 2
11 # _ 2 _ 1 2
11 # 1 2 2
11 # _ 2 _ 2 _ 2
where the segmentation 11 denotes block 11 in the finite element mesh.
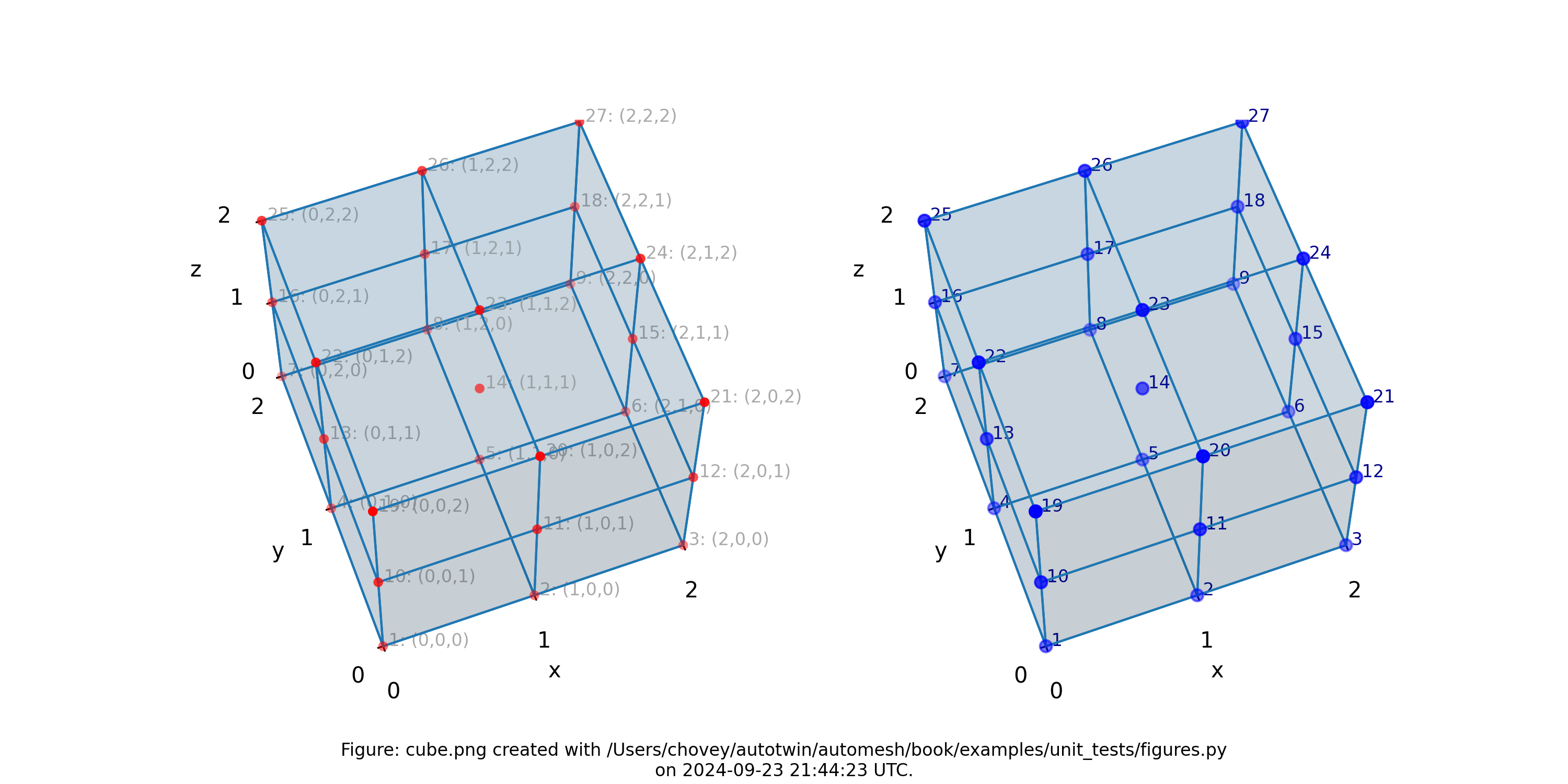
Figure: Mesh composed of one block with eight elements, (left) lattice node numbers, (right) mesh node numbers.
Cube with Multi Blocks and Void
82 # x:1 y:1 z:1
2 # _ 2 _ 1 1
2 # 1 2 1
2 # _ 2 _ 2 _ 1
0 # 1 1 2
31 # _ 2 _ 1 2
0 # 1 2 2
44 # _ 2 _ 2 _ 2
where the segmentation 82, 2, 31 and 44 denotes block 82, 2, 31
and 44, respectively, in the finite element mesh, and segmentation 0 will
be included from the finite element mesh.
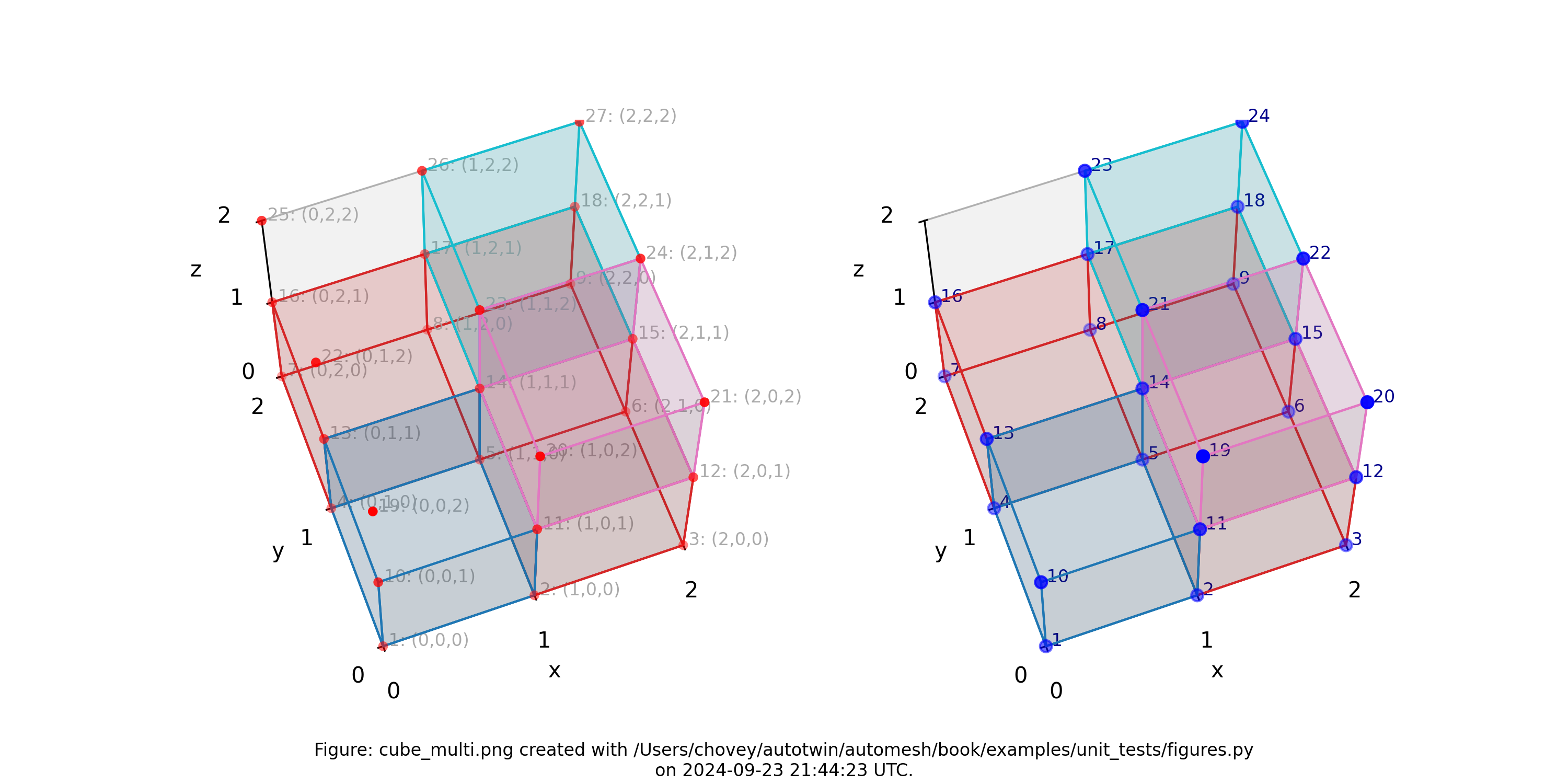
Figure: Mesh composed of four blocks (block 82 has one element, block 2
has three elements, block 31 has one element, and block 44 has one
element), (left) lattice node numbers, (right) mesh node numbers.
Cube with Inclusion
11 # x:1 y:1 z:1
11 # 2 1 1
11 # _ 3 _ 1 1
11 # 1 2 1
11 # 2 2 1
11 # _ 3 _ 2 1
11 # 1 3 1
11 # 2 3 1
11 # _ 3 _ 3 _ 1
11 # 1 1 2
11 # 2 1 2
11 # _ 3 _ 1 2
11 # 1 2 2
88 # 2 2 2
11 # _ 3 _ 2 2
11 # 1 3 2
11 # 2 3 2
11 # _ 3 _ 3 _ 2
11 # 1 1 3
11 # 2 1 3
11 # _ 3 _ 1 3
11 # 1 2 3
11 # 2 2 3
11 # _ 3 _ 2 3
11 # 1 3 3
11 # 2 3 3
11 # _ 3 _ 3 _ 3
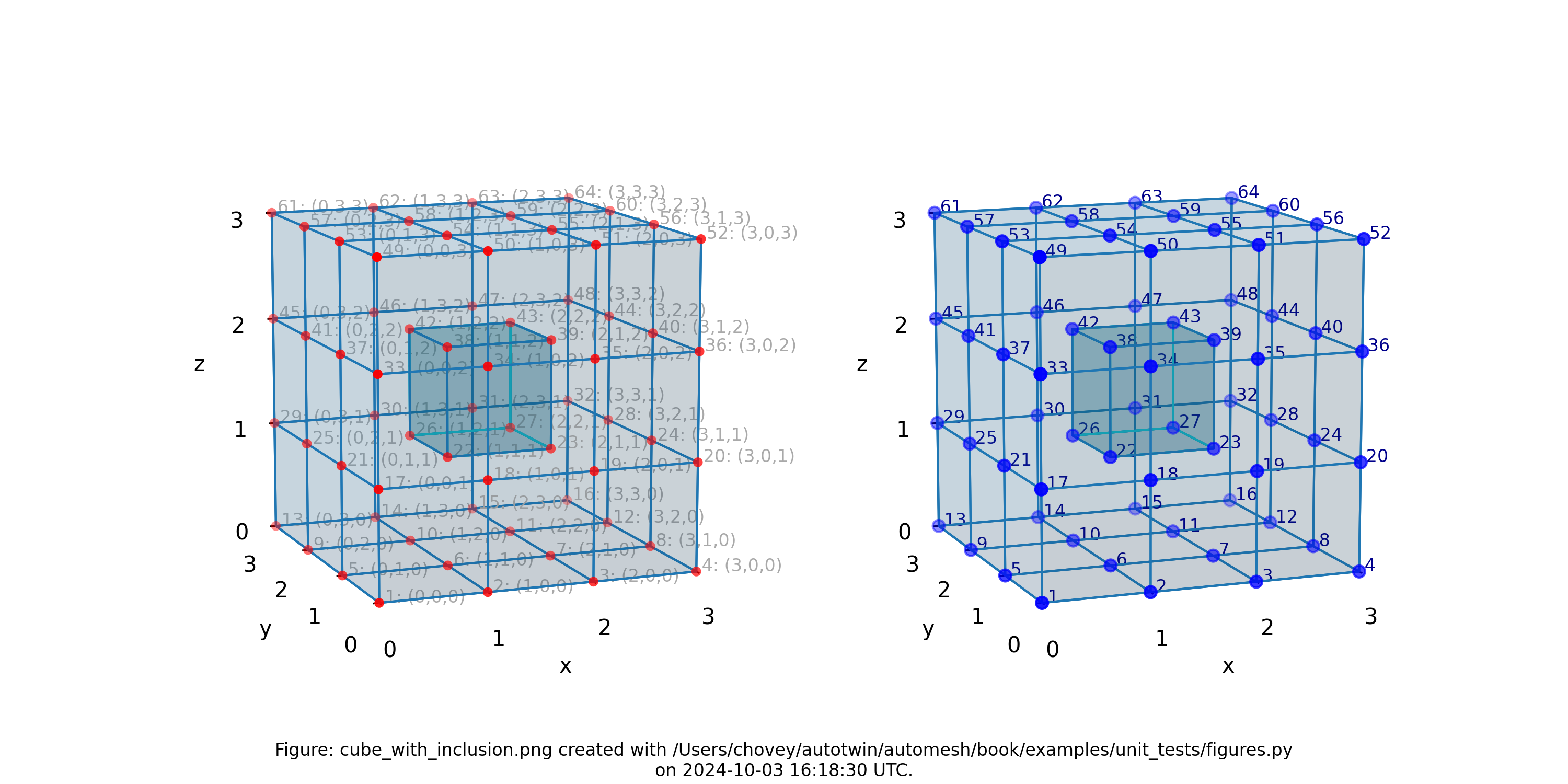
Figure: Mesh composed of 26 voxels of (block 11) and one voxel inslusion
(block 88), (left) lattice node numbers, (right) mesh node numbers.
Bracket
1 # x:1 y:1 z:1
1 # 2 1 1
1 # 3 1 1
1 # _ 4 _ 1 1
1 # x:1 y:2 z:1
1 # 2 2 1
1 # 3 2 1
1 # _ 4 _ 2 1
1 # x:1 y:3 z:1
1 # 2 3 1
0 # 3 3 1
0 # _ 4 _ 3 1
1 # x:1 y:4 z:1
1 # 2 4 1
0 # 3 4 1
0 # _ 4 _ 4 1
where the segmentation 1 denotes block 1 in the finite element mesh,
and segmentation 0 is excluded from the mesh.

Figure: Mesh composed of a L-shaped bracket in the xy plane.
Letter F
11 # x:1 y:1 z:1
0 # 2 1 1
0 # _ 3 _ 1 1
11 # 1 2 1
0 # 2 2 1
0 # _ 3 _ 2 1
11 # 1 3 1
11 # 2 3 1
0 # _ 3 _ 3 1
11 # 1 4 1
0 # 2 4 1
0 # _ 3 _ 4 1
11 # 1 5 1
11 # 2 5 1
11 # _ 3 _ 5 _ 1
where the segmentation 11 denotes block 11 in the finite element mesh.
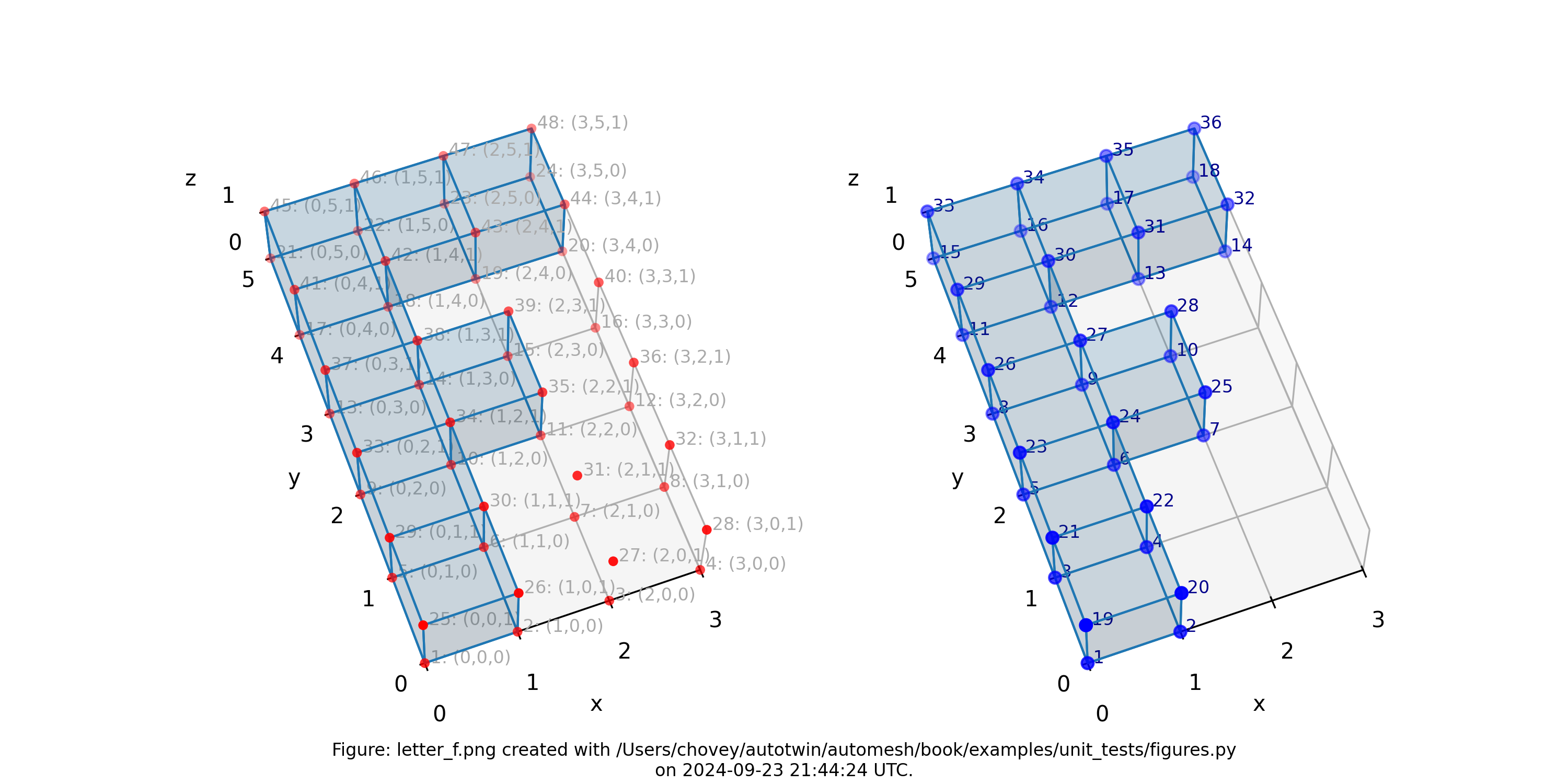
Figure: Mesh composed of a single block with eight elements, (left) lattice node numbers, (right) mesh node numbers.
Letter F in 3D
1 # x:1 y:1 z:1
1 # 2 1 1
1 # 3 1 1
1 # _ 4 _ 1 1
1 # 1 2 1
1 # 2 2 1
1 # 3 2 1
1 # _ 4 _ 2 1
1 # 1 3 1
1 # 2 3 1
1 # 3 3 1
1 # _ 4 _ 3 1
1 # 1 4 1
1 # 2 4 1
1 # 3 4 1
1 # _ 4 _ 4 1
1 # 1 5 1
1 # 2 5 1
1 # 3 5 1
1 # _ 4 _ 5 _ 1
1 # x:1 y:1 z:2
0 # 2 1 2
0 # 3 1 2
0 # _ 4 _ 1 2
1 # 1 2 2
0 # 2 2 2
0 # 3 2 2
0 # _ 4 _ 2 2
1 # 1 3 2
1 # 2 3 2
1 # 3 3 2
1 # _ 4 _ 3 2
1 # 1 4 2
0 # 2 4 2
0 # 3 4 2
0 # _ 4 _ 4 2
1 # 1 5 2
1 # 2 5 2
1 # 3 5 2
1 # _ 4 _ 5 _ 2
1 # x:1 y:1 z:3
0 # 2 1 j
0 # 3 1 2
0 # _ 4 _ 1 2
1 # 1 2 3
0 # 2 2 3
0 # 3 2 3
0 # _ 4 _ 2 3
1 # 1 3 3
0 # 2 3 3
0 # 3 3 3
0 # _ 4 _ 3 3
1 # 1 4 3
0 # 2 4 3
0 # 3 4 3
0 # _ 4 _ 4 3
1 # 1 5 3
1 # 2 5 3
1 # 3 5 3
1 # _ 4 _ 5 _ 3
which corresponds to --nelx 4, --nely 5, and --nelz 3 in the
command line interface.
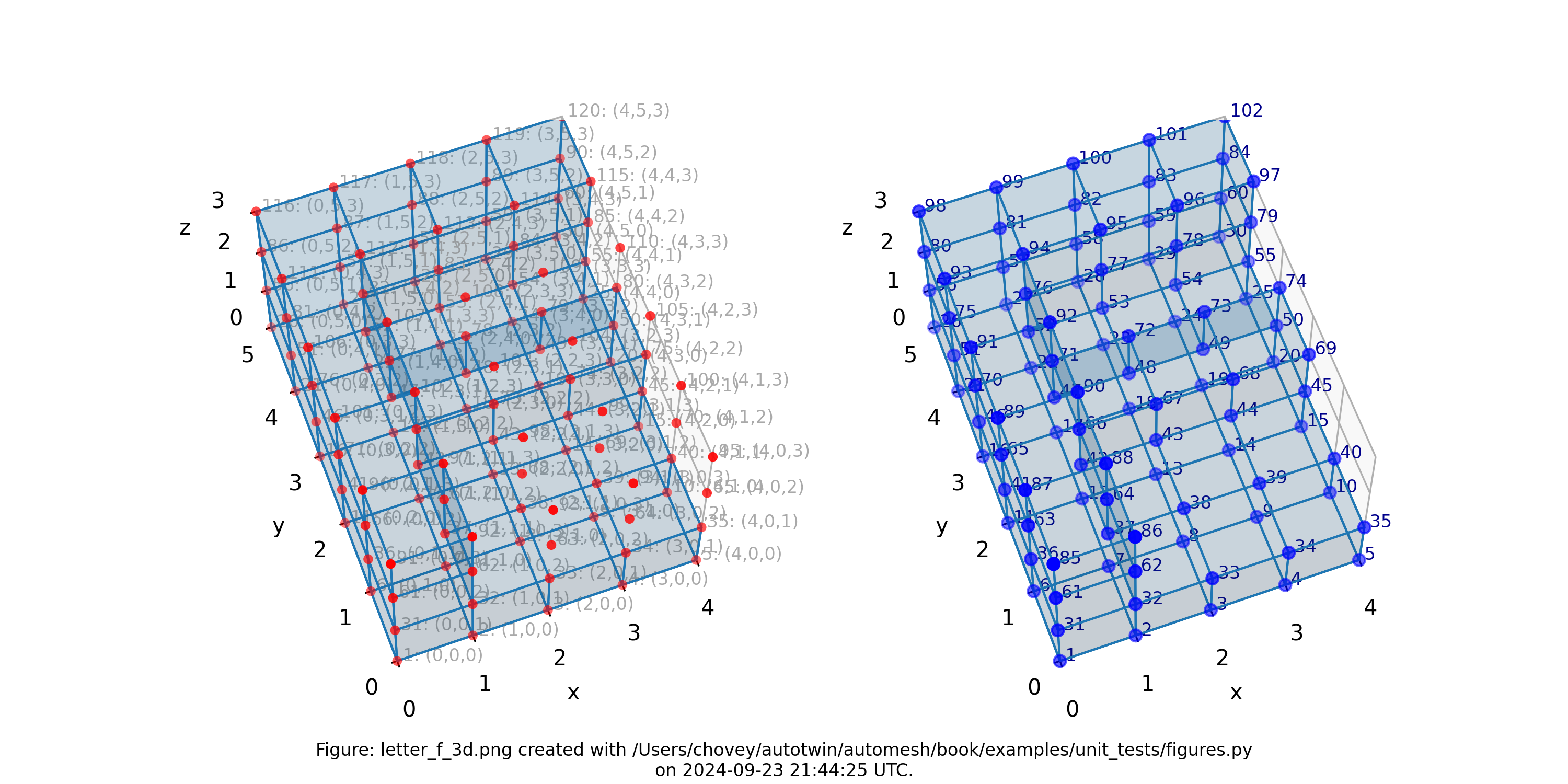
Figure: Mesh composed of a single block with thirty-nine elements, (left) lattice node numbers, (right) mesh node numbers.
The shape of the solid segmentation is more easily seen without the lattice and element nodes, and with decreased opacity, as shown below:

Figure: Mesh composed of a single block with thirty-nine elements, shown with decreased opacity and without lattice and element node numbers.
Sparse
0 # x:1 y:1 z:1
0 # 2 1 1
0 # 3 1 1
0 # 4 1 1
2 # _ 5 _ 1 1
0 # 1 2 1
1 # 2 2 1
0 # 3 2 1
0 # 4 2 1
2 # _ 5 _ 2 1
1 # 1 3 1
2 # 2 3 1
0 # 3 3 1
2 # 4 3 1
0 # _ 5 _ 3 1
0 # 1 4 1
1 # 2 4 1
0 # 3 4 1
2 # 4 4 1
0 # _ 5 _ 4 1
1 # 1 5 1
0 # 2 5 1
0 # 3 5 1
0 # 4 5 1
1 # _ 5 _ 5 _ 1
2 # x:1 y:1 z:2
0 # 2 1 2
2 # 3 1 2
0 # 4 1 2
0 # _ 5 _ 1 2
1 # 1 2 2
1 # 2 2 2
0 # 3 2 2
2 # 4 2 2
2 # _ 5 _ 2 2
2 # 1 3 2
0 # 2 3 2
0 # 3 3 2
0 # 4 3 2
0 # _ 5 _ 3 2
1 # 1 4 2
0 # 2 4 2
0 # 3 4 2
2 # 4 4 2
0 # _ 5 _ 4 2
2 # 1 5 2
0 # 2 5 2
2 # 3 5 2
0 # 4 5 2
2 # _ 5 _ 5 _ 2
0 # x:1 y:1 z:3
0 # 2 1 3
1 # 3 1 3
0 # 4 1 3
2 # _ 5 _ 1 3
0 # 1 2 3
0 # 2 2 3
0 # 3 2 3
1 # 4 2 3
2 # _ 5 _ 2 3
0 # 1 3 3
0 # 2 3 3
2 # 3 3 3
2 # 4 3 3
2 # _ 5 _ 3 3
0 # 1 4 3
0 # 2 4 3
1 # 3 4 3
0 # 4 4 3
1 # _ 5 _ 4 3
0 # 1 5 3
1 # 2 5 3
0 # 3 5 3
1 # 4 5 3
0 # _ 5 _ 5 _ 3
0 # x:1 y:1 z:4
1 # 2 1 4
2 # 3 1 4
1 # 4 1 4
2 # _ 5 _ 1 4
2 # 1 2 4
0 # 2 2 4
2 # 3 2 4
0 # 4 2 4
1 # _ 5 _ 2 4
1 # 1 3 4
2 # 2 3 4
2 # 3 3 4
0 # 4 3 4
0 # _ 5 _ 3 4
2 # 1 4 4
1 # 2 4 4
1 # 3 4 4
1 # 4 4 4
1 # _ 5 _ 4 4
0 # 1 5 4
0 # 2 5 4
1 # 3 5 4
0 # 4 5 4
0 # _ 5 _ 5 _ 4
0 # x:1 y:1 z:5
1 # 2 1 5
0 # 3 1 5
2 # 4 1 5
0 # _ 5 _ 1 5
1 # 1 2 5
0 # 2 2 5
0 # 3 2 5
0 # 4 2 5
2 # _ 5 _ 2 5
0 # 1 3 5
1 # 2 3 5
0 # 3 3 5
0 # 4 3 5
0 # _ 5 _ 3 5
1 # 1 4 5
0 # 2 4 5
0 # 3 4 5
0 # 4 4 5
0 # _ 5 _ 4 5
0 # 1 5 5
0 # 2 5 5
1 # 3 5 5
2 # 4 5 5
1 # _ 5 _ 5 _ 5
where the segmentation 1 denotes block 1 and segmentation 2 denotes block 2 in the finite eelement mesh (with segmentation 0 excluded).
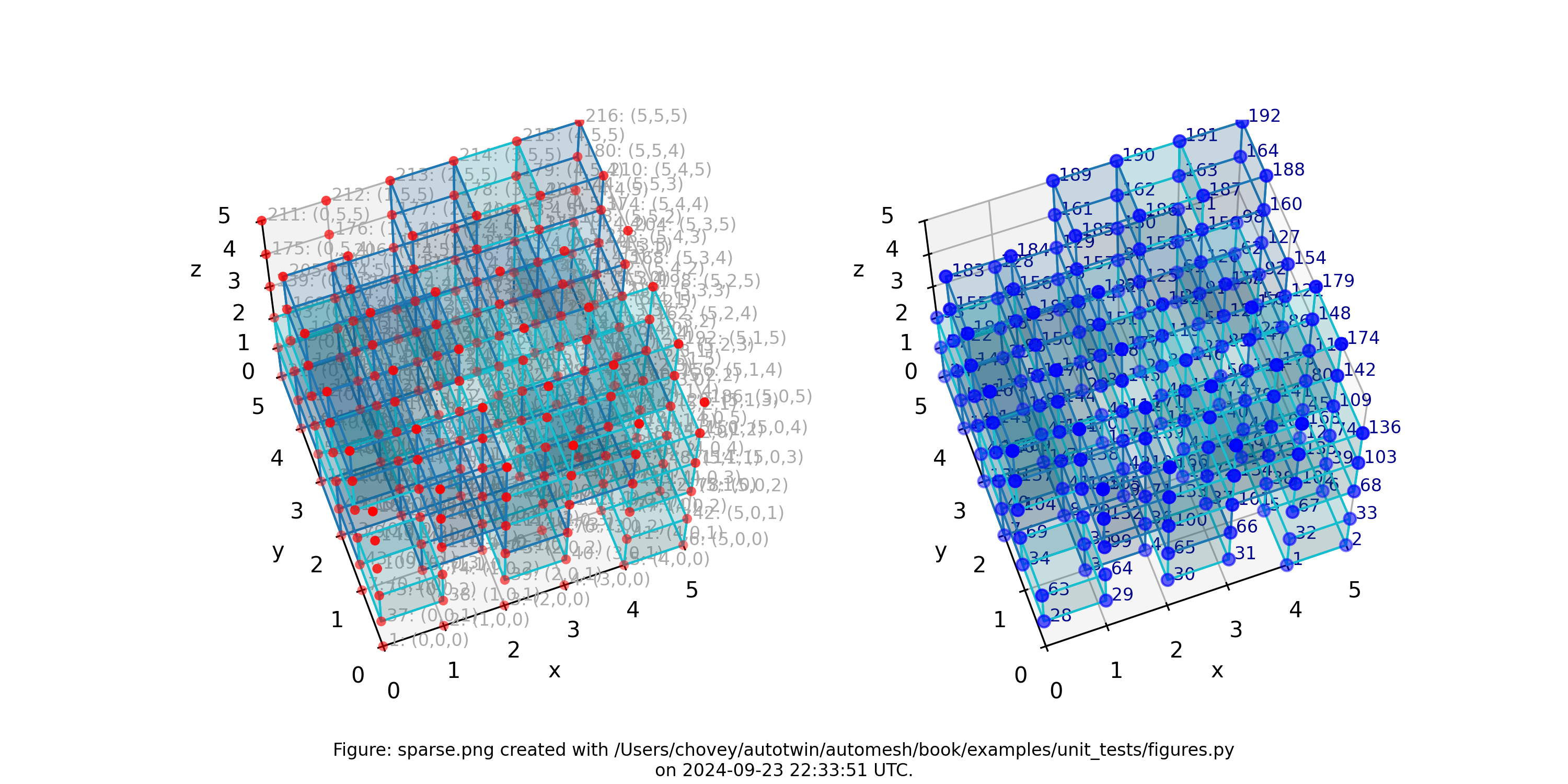
Figure: Sparse mesh composed of two materials at random voxel locations.
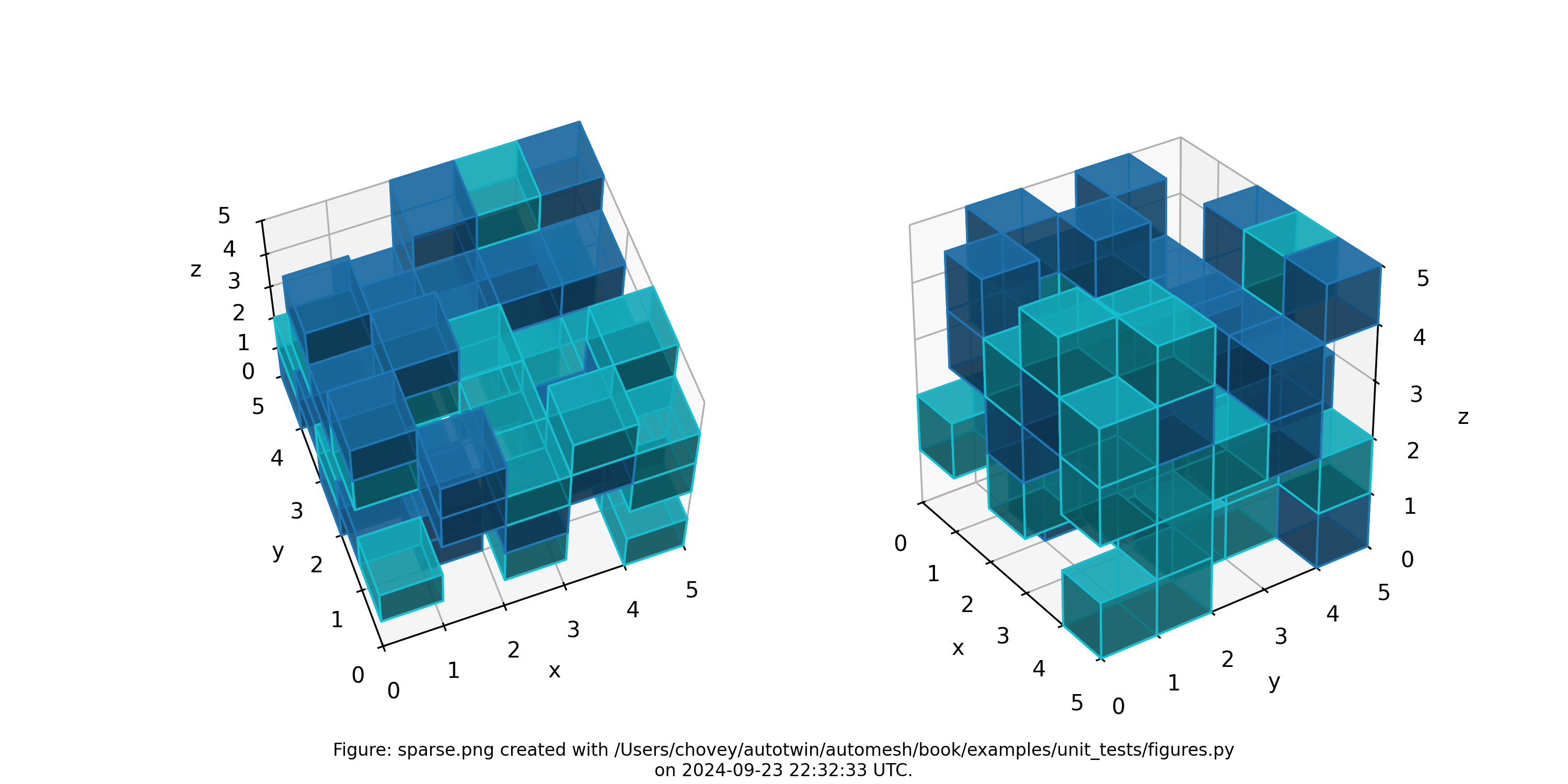
Figure: Sparse mesh composed of two materials at random voxel locations, shown with decreased opactity and without lattice and element node numbers.
Source
The figures were created with the following Python files:
examples_data.py
r"""This module, examples_data.py, contains the data for
the unit test examples.
"""
from typing import Final
import numpy as np
import examples_types as ty
# Type aliases
Example = ty.Example
COMMON_TITLE: Final[str] = "Lattice Index and Coordinates: "
class Single(Example):
"""A specific example of a single voxel."""
figure_title: str = COMMON_TITLE + "Single"
file_stem: str = "single"
segmentation = np.array(
[
[
[
11,
],
],
],
dtype=np.uint8,
)
included_ids = (11,)
gold_lattice = ((1, 2, 4, 3, 5, 6, 8, 7),)
gold_mesh_lattice_connectivity = (
(
11,
(1, 2, 4, 3, 5, 6, 8, 7),
),
)
gold_mesh_element_connectivity = (
(
11,
(1, 2, 4, 3, 5, 6, 8, 7),
),
)
class DoubleX(Example):
"""A specific example of a double voxel, coursed along the x-axis."""
figure_title: str = COMMON_TITLE + "DoubleX"
file_stem: str = "double_x"
segmentation = np.array(
[
[
[
11,
11,
],
],
],
dtype=np.uint8,
)
included_ids = (11,)
gold_lattice = (
(1, 2, 5, 4, 7, 8, 11, 10),
(2, 3, 6, 5, 8, 9, 12, 11),
)
gold_mesh_lattice_connectivity = (
(
11,
(1, 2, 5, 4, 7, 8, 11, 10),
(2, 3, 6, 5, 8, 9, 12, 11),
),
)
gold_mesh_element_connectivity = (
(
11,
(1, 2, 5, 4, 7, 8, 11, 10),
(2, 3, 6, 5, 8, 9, 12, 11),
),
)
class DoubleY(Example):
"""A specific example of a double voxel, coursed along the y-axis."""
figure_title: str = COMMON_TITLE + "DoubleY"
file_stem: str = "double_y"
segmentation = np.array(
[
[
[
11,
],
[
11,
],
],
],
dtype=np.uint8,
)
included_ids = (11,)
gold_lattice = (
(1, 2, 4, 3, 7, 8, 10, 9),
(3, 4, 6, 5, 9, 10, 12, 11),
)
gold_mesh_lattice_connectivity = (
(
11,
(1, 2, 4, 3, 7, 8, 10, 9),
(3, 4, 6, 5, 9, 10, 12, 11),
),
)
gold_mesh_element_connectivity = (
(
11,
(1, 2, 4, 3, 7, 8, 10, 9),
(3, 4, 6, 5, 9, 10, 12, 11),
),
)
class TripleX(Example):
"""A triple voxel lattice, coursed along the x-axis."""
figure_title: str = COMMON_TITLE + "Triple"
file_stem: str = "triple_x"
segmentation = np.array(
[
[
[
11,
11,
11,
],
],
],
dtype=np.uint8,
)
included_ids = (11,)
gold_lattice = (
(1, 2, 6, 5, 9, 10, 14, 13),
(2, 3, 7, 6, 10, 11, 15, 14),
(3, 4, 8, 7, 11, 12, 16, 15),
)
gold_mesh_lattice_connectivity = (
(
11,
(1, 2, 6, 5, 9, 10, 14, 13),
(2, 3, 7, 6, 10, 11, 15, 14),
(3, 4, 8, 7, 11, 12, 16, 15),
),
)
gold_mesh_element_connectivity = (
(
11,
(1, 2, 6, 5, 9, 10, 14, 13),
(2, 3, 7, 6, 10, 11, 15, 14),
(3, 4, 8, 7, 11, 12, 16, 15),
),
)
class QuadrupleX(Example):
"""A quadruple voxel lattice, coursed along the x-axis."""
figure_title: str = COMMON_TITLE + "Quadruple"
file_stem: str = "quadruple_x"
segmentation = np.array(
[
[
[
11,
11,
11,
11,
],
],
],
dtype=np.uint8,
)
included_ids = (11,)
gold_lattice = (
(1, 2, 7, 6, 11, 12, 17, 16),
(2, 3, 8, 7, 12, 13, 18, 17),
(3, 4, 9, 8, 13, 14, 19, 18),
(4, 5, 10, 9, 14, 15, 20, 19),
)
gold_mesh_lattice_connectivity = (
(
11,
(1, 2, 7, 6, 11, 12, 17, 16),
(2, 3, 8, 7, 12, 13, 18, 17),
(3, 4, 9, 8, 13, 14, 19, 18),
(4, 5, 10, 9, 14, 15, 20, 19),
),
)
gold_mesh_element_connectivity = (
(
11,
(1, 2, 7, 6, 11, 12, 17, 16),
(2, 3, 8, 7, 12, 13, 18, 17),
(3, 4, 9, 8, 13, 14, 19, 18),
(4, 5, 10, 9, 14, 15, 20, 19),
),
)
class Quadruple2VoidsX(Example):
"""A quadruple voxel lattice, coursed along the x-axis, with two
intermediate voxels in the segmentation being void.
"""
figure_title: str = COMMON_TITLE + "Quadruple2VoidsX"
file_stem: str = "quadruple_2_voids_x"
segmentation = np.array(
[
[
[
99,
0,
0,
99,
],
],
],
dtype=np.uint8,
)
included_ids = (99,)
gold_lattice = (
(1, 2, 7, 6, 11, 12, 17, 16),
(2, 3, 8, 7, 12, 13, 18, 17),
(3, 4, 9, 8, 13, 14, 19, 18),
(4, 5, 10, 9, 14, 15, 20, 19),
)
gold_mesh_lattice_connectivity = (
(
99,
(1, 2, 7, 6, 11, 12, 17, 16),
(4, 5, 10, 9, 14, 15, 20, 19),
),
)
gold_mesh_element_connectivity = (
(
99,
(1, 2, 6, 5, 9, 10, 14, 13),
(3, 4, 8, 7, 11, 12, 16, 15),
),
)
class Quadruple2Blocks(Example):
"""A quadruple voxel lattice, with the first intermediate voxel being
the second block and the second intermediate voxel being void.
"""
figure_title: str = COMMON_TITLE + "Quadruple2Blocks"
file_stem: str = "quadruple_2_blocks"
segmentation = np.array(
[
[
[
100,
101,
101,
100,
],
],
],
dtype=np.uint8,
)
included_ids = (
100,
101,
)
gold_lattice = (
(1, 2, 7, 6, 11, 12, 17, 16),
(2, 3, 8, 7, 12, 13, 18, 17),
(3, 4, 9, 8, 13, 14, 19, 18),
(4, 5, 10, 9, 14, 15, 20, 19),
)
gold_mesh_lattice_connectivity = (
(
100,
(1, 2, 7, 6, 11, 12, 17, 16),
(4, 5, 10, 9, 14, 15, 20, 19),
),
(
101,
(2, 3, 8, 7, 12, 13, 18, 17),
(3, 4, 9, 8, 13, 14, 19, 18),
),
)
gold_mesh_element_connectivity = (
(
100,
(1, 2, 7, 6, 11, 12, 17, 16),
(4, 5, 10, 9, 14, 15, 20, 19),
),
(
101,
(2, 3, 8, 7, 12, 13, 18, 17),
(3, 4, 9, 8, 13, 14, 19, 18),
),
)
class Quadruple2BlocksVoid(Example):
"""A quadruple voxel lattice, with the first intermediate voxel being
the second block and the second intermediate voxel being void.
"""
figure_title: str = COMMON_TITLE + "Quadruple2BlocksVoid"
file_stem: str = "quadruple_2_blocks_void"
segmentation = np.array(
[
[
[
102,
103,
0,
102,
],
],
],
dtype=np.uint8,
)
included_ids = (
102,
103,
)
gold_lattice = (
(1, 2, 7, 6, 11, 12, 17, 16),
(2, 3, 8, 7, 12, 13, 18, 17),
(3, 4, 9, 8, 13, 14, 19, 18),
(4, 5, 10, 9, 14, 15, 20, 19),
)
gold_mesh_lattice_connectivity = (
(
102,
(1, 2, 7, 6, 11, 12, 17, 16),
(4, 5, 10, 9, 14, 15, 20, 19),
),
(
103,
(2, 3, 8, 7, 12, 13, 18, 17),
),
)
gold_mesh_element_connectivity = (
(
102,
(1, 2, 7, 6, 11, 12, 17, 16),
(4, 5, 10, 9, 14, 15, 20, 19),
),
(
103,
(2, 3, 8, 7, 12, 13, 18, 17),
),
)
class Cube(Example):
"""A (2 x 2 x 2) voxel cube."""
figure_title: str = COMMON_TITLE + "Cube"
file_stem: str = "cube"
segmentation = np.array(
[
[
[
11,
11,
],
[
11,
11,
],
],
[
[
11,
11,
],
[
11,
11,
],
],
],
dtype=np.uint8,
)
included_ids = (11,)
gold_lattice = (
(1, 2, 5, 4, 10, 11, 14, 13),
(2, 3, 6, 5, 11, 12, 15, 14),
(4, 5, 8, 7, 13, 14, 17, 16),
(5, 6, 9, 8, 14, 15, 18, 17),
(10, 11, 14, 13, 19, 20, 23, 22),
(11, 12, 15, 14, 20, 21, 24, 23),
(13, 14, 17, 16, 22, 23, 26, 25),
(14, 15, 18, 17, 23, 24, 27, 26),
)
gold_mesh_lattice_connectivity = (
(
11,
(1, 2, 5, 4, 10, 11, 14, 13),
(2, 3, 6, 5, 11, 12, 15, 14),
(4, 5, 8, 7, 13, 14, 17, 16),
(5, 6, 9, 8, 14, 15, 18, 17),
(10, 11, 14, 13, 19, 20, 23, 22),
(11, 12, 15, 14, 20, 21, 24, 23),
(13, 14, 17, 16, 22, 23, 26, 25),
(14, 15, 18, 17, 23, 24, 27, 26),
),
)
gold_mesh_element_connectivity = (
(
11,
(1, 2, 5, 4, 10, 11, 14, 13),
(2, 3, 6, 5, 11, 12, 15, 14),
(4, 5, 8, 7, 13, 14, 17, 16),
(5, 6, 9, 8, 14, 15, 18, 17),
(10, 11, 14, 13, 19, 20, 23, 22),
(11, 12, 15, 14, 20, 21, 24, 23),
(13, 14, 17, 16, 22, 23, 26, 25),
(14, 15, 18, 17, 23, 24, 27, 26),
),
)
class CubeMulti(Example):
"""A (2 x 2 x 2) voxel cube with two voids and six elements."""
figure_title: str = COMMON_TITLE + "CubeMulti"
file_stem: str = "cube_multi"
segmentation = np.array(
[
[
[
82,
2,
],
[
2,
2,
],
],
[
[
0,
31,
],
[
0,
44,
],
],
],
dtype=np.uint8,
)
included_ids = (
82,
2,
31,
44,
)
gold_lattice = (
(1, 2, 5, 4, 10, 11, 14, 13),
(2, 3, 6, 5, 11, 12, 15, 14),
(4, 5, 8, 7, 13, 14, 17, 16),
(5, 6, 9, 8, 14, 15, 18, 17),
(10, 11, 14, 13, 19, 20, 23, 22),
(11, 12, 15, 14, 20, 21, 24, 23),
(13, 14, 17, 16, 22, 23, 26, 25),
(14, 15, 18, 17, 23, 24, 27, 26),
)
gold_mesh_lattice_connectivity = (
# (
# 0,
# (10, 11, 14, 13, 19, 20, 23, 22),
# ),
# (
# 0,
# (13, 14, 17, 16, 22, 23, 26, 25),
(
2,
(2, 3, 6, 5, 11, 12, 15, 14),
(4, 5, 8, 7, 13, 14, 17, 16),
(5, 6, 9, 8, 14, 15, 18, 17),
),
(
31,
(11, 12, 15, 14, 20, 21, 24, 23),
),
(
44,
(14, 15, 18, 17, 23, 24, 27, 26),
),
(
82,
(1, 2, 5, 4, 10, 11, 14, 13),
),
)
gold_mesh_element_connectivity = (
(
2,
(2, 3, 6, 5, 11, 12, 15, 14),
(4, 5, 8, 7, 13, 14, 17, 16),
(5, 6, 9, 8, 14, 15, 18, 17),
),
(
31,
(11, 12, 15, 14, 19, 20, 22, 21),
),
(
44,
(14, 15, 18, 17, 21, 22, 24, 23),
),
(
82,
(1, 2, 5, 4, 10, 11, 14, 13),
),
)
class CubeWithInclusion(Example):
"""A (3 x 3 x 3) voxel cube with a single voxel inclusion
at the center.
"""
figure_title: str = COMMON_TITLE + "CubeWithInclusion"
file_stem: str = "cube_with_inclusion"
segmentation = np.array(
[
[
[
11,
11,
11,
],
[
11,
11,
11,
],
[
11,
11,
11,
],
],
[
[
11,
11,
11,
],
[
11,
88,
11,
],
[
11,
11,
11,
],
],
[
[
11,
11,
11,
],
[
11,
11,
11,
],
[
11,
11,
11,
],
],
],
dtype=np.uint8,
)
included_ids = (
11,
88,
)
gold_lattice = (
(1, 2, 6, 5, 17, 18, 22, 21),
(2, 3, 7, 6, 18, 19, 23, 22),
(3, 4, 8, 7, 19, 20, 24, 23),
(5, 6, 10, 9, 21, 22, 26, 25),
(6, 7, 11, 10, 22, 23, 27, 26),
(7, 8, 12, 11, 23, 24, 28, 27),
(9, 10, 14, 13, 25, 26, 30, 29),
(10, 11, 15, 14, 26, 27, 31, 30),
(11, 12, 16, 15, 27, 28, 32, 31),
(17, 18, 22, 21, 33, 34, 38, 37),
(18, 19, 23, 22, 34, 35, 39, 38),
(19, 20, 24, 23, 35, 36, 40, 39),
(21, 22, 26, 25, 37, 38, 42, 41),
(22, 23, 27, 26, 38, 39, 43, 42),
(23, 24, 28, 27, 39, 40, 44, 43),
(25, 26, 30, 29, 41, 42, 46, 45),
(26, 27, 31, 30, 42, 43, 47, 46),
(27, 28, 32, 31, 43, 44, 48, 47),
(33, 34, 38, 37, 49, 50, 54, 53),
(34, 35, 39, 38, 50, 51, 55, 54),
(35, 36, 40, 39, 51, 52, 56, 55),
(37, 38, 42, 41, 53, 54, 58, 57),
(38, 39, 43, 42, 54, 55, 59, 58),
(39, 40, 44, 43, 55, 56, 60, 59),
(41, 42, 46, 45, 57, 58, 62, 61),
(42, 43, 47, 46, 58, 59, 63, 62),
(43, 44, 48, 47, 59, 60, 64, 63),
)
gold_mesh_lattice_connectivity = (
(
11,
(1, 2, 6, 5, 17, 18, 22, 21),
(2, 3, 7, 6, 18, 19, 23, 22),
(3, 4, 8, 7, 19, 20, 24, 23),
(5, 6, 10, 9, 21, 22, 26, 25),
(6, 7, 11, 10, 22, 23, 27, 26),
(7, 8, 12, 11, 23, 24, 28, 27),
(9, 10, 14, 13, 25, 26, 30, 29),
(10, 11, 15, 14, 26, 27, 31, 30),
(11, 12, 16, 15, 27, 28, 32, 31),
(17, 18, 22, 21, 33, 34, 38, 37),
(18, 19, 23, 22, 34, 35, 39, 38),
(19, 20, 24, 23, 35, 36, 40, 39),
(21, 22, 26, 25, 37, 38, 42, 41),
(23, 24, 28, 27, 39, 40, 44, 43),
(25, 26, 30, 29, 41, 42, 46, 45),
(26, 27, 31, 30, 42, 43, 47, 46),
(27, 28, 32, 31, 43, 44, 48, 47),
(33, 34, 38, 37, 49, 50, 54, 53),
(34, 35, 39, 38, 50, 51, 55, 54),
(35, 36, 40, 39, 51, 52, 56, 55),
(37, 38, 42, 41, 53, 54, 58, 57),
(38, 39, 43, 42, 54, 55, 59, 58),
(39, 40, 44, 43, 55, 56, 60, 59),
(41, 42, 46, 45, 57, 58, 62, 61),
(42, 43, 47, 46, 58, 59, 63, 62),
(43, 44, 48, 47, 59, 60, 64, 63),
),
(
88,
(22, 23, 27, 26, 38, 39, 43, 42),
),
)
gold_mesh_element_connectivity = (
(
11,
(1, 2, 6, 5, 17, 18, 22, 21),
(2, 3, 7, 6, 18, 19, 23, 22),
(3, 4, 8, 7, 19, 20, 24, 23),
(5, 6, 10, 9, 21, 22, 26, 25),
(6, 7, 11, 10, 22, 23, 27, 26),
(7, 8, 12, 11, 23, 24, 28, 27),
(9, 10, 14, 13, 25, 26, 30, 29),
(10, 11, 15, 14, 26, 27, 31, 30),
(11, 12, 16, 15, 27, 28, 32, 31),
(17, 18, 22, 21, 33, 34, 38, 37),
(18, 19, 23, 22, 34, 35, 39, 38),
(19, 20, 24, 23, 35, 36, 40, 39),
(21, 22, 26, 25, 37, 38, 42, 41),
(23, 24, 28, 27, 39, 40, 44, 43),
(25, 26, 30, 29, 41, 42, 46, 45),
(26, 27, 31, 30, 42, 43, 47, 46),
(27, 28, 32, 31, 43, 44, 48, 47),
(33, 34, 38, 37, 49, 50, 54, 53),
(34, 35, 39, 38, 50, 51, 55, 54),
(35, 36, 40, 39, 51, 52, 56, 55),
(37, 38, 42, 41, 53, 54, 58, 57),
(38, 39, 43, 42, 54, 55, 59, 58),
(39, 40, 44, 43, 55, 56, 60, 59),
(41, 42, 46, 45, 57, 58, 62, 61),
(42, 43, 47, 46, 58, 59, 63, 62),
(43, 44, 48, 47, 59, 60, 64, 63),
),
(
88,
(22, 23, 27, 26, 38, 39, 43, 42),
),
)
class Bracket(Example):
"""An L-shape bracket in the xy plane."""
figure_title: str = COMMON_TITLE + "Bracket"
file_stem: str = "bracket"
segmentation = np.array(
[
[
[1, 1, 1, 1],
[1, 1, 1, 1],
[1, 1, 0, 0],
[1, 1, 0, 0],
],
]
)
included_ids = (1,)
gold_lattice = (
(1, 2, 7, 6, 26, 27, 32, 31),
(2, 3, 8, 7, 27, 28, 33, 32),
(3, 4, 9, 8, 28, 29, 34, 33),
(4, 5, 10, 9, 29, 30, 35, 34),
(6, 7, 12, 11, 31, 32, 37, 36),
(7, 8, 13, 12, 32, 33, 38, 37),
(8, 9, 14, 13, 33, 34, 39, 38),
(9, 10, 15, 14, 34, 35, 40, 39),
(11, 12, 17, 16, 36, 37, 42, 41),
(12, 13, 18, 17, 37, 38, 43, 42),
(13, 14, 19, 18, 38, 39, 44, 43),
(14, 15, 20, 19, 39, 40, 45, 44),
(16, 17, 22, 21, 41, 42, 47, 46),
(17, 18, 23, 22, 42, 43, 48, 47),
(18, 19, 24, 23, 43, 44, 49, 48),
(19, 20, 25, 24, 44, 45, 50, 49),
)
gold_mesh_lattice_connectivity = (
(
1,
(1, 2, 7, 6, 26, 27, 32, 31),
(2, 3, 8, 7, 27, 28, 33, 32),
(3, 4, 9, 8, 28, 29, 34, 33),
(4, 5, 10, 9, 29, 30, 35, 34),
(6, 7, 12, 11, 31, 32, 37, 36),
(7, 8, 13, 12, 32, 33, 38, 37),
(8, 9, 14, 13, 33, 34, 39, 38),
(9, 10, 15, 14, 34, 35, 40, 39),
(11, 12, 17, 16, 36, 37, 42, 41),
(12, 13, 18, 17, 37, 38, 43, 42),
(16, 17, 22, 21, 41, 42, 47, 46),
(17, 18, 23, 22, 42, 43, 48, 47),
),
)
gold_mesh_element_connectivity = (
(
1,
(1, 2, 7, 6, 22, 23, 28, 27),
(2, 3, 8, 7, 23, 24, 29, 28),
(3, 4, 9, 8, 24, 25, 30, 29),
(4, 5, 10, 9, 25, 26, 31, 30),
(6, 7, 12, 11, 27, 28, 33, 32),
(7, 8, 13, 12, 28, 29, 34, 33),
(8, 9, 14, 13, 29, 30, 35, 34),
(9, 10, 15, 14, 30, 31, 36, 35),
(11, 12, 17, 16, 32, 33, 38, 37),
(12, 13, 18, 17, 33, 34, 39, 38),
(16, 17, 20, 19, 37, 38, 41, 40),
(17, 18, 21, 20, 38, 39, 42, 41),
),
)
class LetterF(Example):
"""A minimal letter F example."""
figure_title: str = COMMON_TITLE + "LetterF"
file_stem: str = "letter_f"
segmentation = np.array(
[
[
[
11,
0,
0,
],
[
11,
0,
0,
],
[
11,
11,
0,
],
[
11,
0,
0,
],
[
11,
11,
11,
],
],
],
dtype=np.uint8,
)
included_ids = (11,)
gold_lattice = (
(1, 2, 6, 5, 25, 26, 30, 29),
(2, 3, 7, 6, 26, 27, 31, 30),
(3, 4, 8, 7, 27, 28, 32, 31),
(5, 6, 10, 9, 29, 30, 34, 33),
(6, 7, 11, 10, 30, 31, 35, 34),
(7, 8, 12, 11, 31, 32, 36, 35),
(9, 10, 14, 13, 33, 34, 38, 37),
(10, 11, 15, 14, 34, 35, 39, 38),
(11, 12, 16, 15, 35, 36, 40, 39),
(13, 14, 18, 17, 37, 38, 42, 41),
(14, 15, 19, 18, 38, 39, 43, 42),
(15, 16, 20, 19, 39, 40, 44, 43),
(17, 18, 22, 21, 41, 42, 46, 45),
(18, 19, 23, 22, 42, 43, 47, 46),
(19, 20, 24, 23, 43, 44, 48, 47),
)
gold_mesh_lattice_connectivity = (
(
11,
(1, 2, 6, 5, 25, 26, 30, 29),
# (2, 3, 7, 6, 26, 27, 31, 30),
# (3, 4, 8, 7, 27, 28, 32, 31),
(5, 6, 10, 9, 29, 30, 34, 33),
# (6, 7, 11, 10, 30, 31, 35, 34),
# (7, 8, 12, 11, 31, 32, 36, 35),
(9, 10, 14, 13, 33, 34, 38, 37),
(10, 11, 15, 14, 34, 35, 39, 38),
# (11, 12, 16, 15, 35, 36, 40, 39),
(13, 14, 18, 17, 37, 38, 42, 41),
# (14, 15, 19, 18, 38, 39, 43, 42),
# (15, 16, 20, 19, 39, 40, 44, 43),
(17, 18, 22, 21, 41, 42, 46, 45),
(18, 19, 23, 22, 42, 43, 47, 46),
(19, 20, 24, 23, 43, 44, 48, 47),
),
)
gold_mesh_element_connectivity = (
(
11,
(1, 2, 4, 3, 19, 20, 22, 21),
#
#
(3, 4, 6, 5, 21, 22, 24, 23),
#
#
(5, 6, 9, 8, 23, 24, 27, 26),
(6, 7, 10, 9, 24, 25, 28, 27),
#
(8, 9, 12, 11, 26, 27, 30, 29),
#
#
(11, 12, 16, 15, 29, 30, 34, 33),
(12, 13, 17, 16, 30, 31, 35, 34),
(13, 14, 18, 17, 31, 32, 36, 35),
),
)
class LetterF3D(Example):
"""A three dimensional variation of the letter F, in a non-standard
orientation.
"""
figure_title: str = COMMON_TITLE + "LetterF3D"
file_stem: str = "letter_f_3d"
segmentation = np.array(
[
[
[1, 1, 1, 1],
[1, 1, 1, 1],
[1, 1, 1, 1],
[1, 1, 1, 1],
[1, 1, 1, 1],
],
[
[1, 0, 0, 0],
[1, 0, 0, 0],
[1, 1, 1, 1],
[1, 0, 0, 0],
[1, 1, 1, 1],
],
[
[1, 0, 0, 0],
[1, 0, 0, 0],
[1, 0, 0, 0],
[1, 0, 0, 0],
[1, 1, 1, 1],
],
],
dtype=np.uint8,
)
included_ids = (1,)
gold_lattice = (
(1, 2, 7, 6, 31, 32, 37, 36),
(2, 3, 8, 7, 32, 33, 38, 37),
(3, 4, 9, 8, 33, 34, 39, 38),
(4, 5, 10, 9, 34, 35, 40, 39),
(6, 7, 12, 11, 36, 37, 42, 41),
(7, 8, 13, 12, 37, 38, 43, 42),
(8, 9, 14, 13, 38, 39, 44, 43),
(9, 10, 15, 14, 39, 40, 45, 44),
(11, 12, 17, 16, 41, 42, 47, 46),
(12, 13, 18, 17, 42, 43, 48, 47),
(13, 14, 19, 18, 43, 44, 49, 48),
(14, 15, 20, 19, 44, 45, 50, 49),
(16, 17, 22, 21, 46, 47, 52, 51),
(17, 18, 23, 22, 47, 48, 53, 52),
(18, 19, 24, 23, 48, 49, 54, 53),
(19, 20, 25, 24, 49, 50, 55, 54),
(21, 22, 27, 26, 51, 52, 57, 56),
(22, 23, 28, 27, 52, 53, 58, 57),
(23, 24, 29, 28, 53, 54, 59, 58),
(24, 25, 30, 29, 54, 55, 60, 59),
(31, 32, 37, 36, 61, 62, 67, 66),
(32, 33, 38, 37, 62, 63, 68, 67),
(33, 34, 39, 38, 63, 64, 69, 68),
(34, 35, 40, 39, 64, 65, 70, 69),
(36, 37, 42, 41, 66, 67, 72, 71),
(37, 38, 43, 42, 67, 68, 73, 72),
(38, 39, 44, 43, 68, 69, 74, 73),
(39, 40, 45, 44, 69, 70, 75, 74),
(41, 42, 47, 46, 71, 72, 77, 76),
(42, 43, 48, 47, 72, 73, 78, 77),
(43, 44, 49, 48, 73, 74, 79, 78),
(44, 45, 50, 49, 74, 75, 80, 79),
(46, 47, 52, 51, 76, 77, 82, 81),
(47, 48, 53, 52, 77, 78, 83, 82),
(48, 49, 54, 53, 78, 79, 84, 83),
(49, 50, 55, 54, 79, 80, 85, 84),
(51, 52, 57, 56, 81, 82, 87, 86),
(52, 53, 58, 57, 82, 83, 88, 87),
(53, 54, 59, 58, 83, 84, 89, 88),
(54, 55, 60, 59, 84, 85, 90, 89),
(61, 62, 67, 66, 91, 92, 97, 96),
(62, 63, 68, 67, 92, 93, 98, 97),
(63, 64, 69, 68, 93, 94, 99, 98),
(64, 65, 70, 69, 94, 95, 100, 99),
(66, 67, 72, 71, 96, 97, 102, 101),
(67, 68, 73, 72, 97, 98, 103, 102),
(68, 69, 74, 73, 98, 99, 104, 103),
(69, 70, 75, 74, 99, 100, 105, 104),
(71, 72, 77, 76, 101, 102, 107, 106),
(72, 73, 78, 77, 102, 103, 108, 107),
(73, 74, 79, 78, 103, 104, 109, 108),
(74, 75, 80, 79, 104, 105, 110, 109),
(76, 77, 82, 81, 106, 107, 112, 111),
(77, 78, 83, 82, 107, 108, 113, 112),
(78, 79, 84, 83, 108, 109, 114, 113),
(79, 80, 85, 84, 109, 110, 115, 114),
(81, 82, 87, 86, 111, 112, 117, 116),
(82, 83, 88, 87, 112, 113, 118, 117),
(83, 84, 89, 88, 113, 114, 119, 118),
(84, 85, 90, 89, 114, 115, 120, 119),
)
gold_mesh_lattice_connectivity = (
(
1,
(1, 2, 7, 6, 31, 32, 37, 36),
(2, 3, 8, 7, 32, 33, 38, 37),
(3, 4, 9, 8, 33, 34, 39, 38),
(4, 5, 10, 9, 34, 35, 40, 39),
(6, 7, 12, 11, 36, 37, 42, 41),
(7, 8, 13, 12, 37, 38, 43, 42),
(8, 9, 14, 13, 38, 39, 44, 43),
(9, 10, 15, 14, 39, 40, 45, 44),
(11, 12, 17, 16, 41, 42, 47, 46),
(12, 13, 18, 17, 42, 43, 48, 47),
(13, 14, 19, 18, 43, 44, 49, 48),
(14, 15, 20, 19, 44, 45, 50, 49),
(16, 17, 22, 21, 46, 47, 52, 51),
(17, 18, 23, 22, 47, 48, 53, 52),
(18, 19, 24, 23, 48, 49, 54, 53),
(19, 20, 25, 24, 49, 50, 55, 54),
(21, 22, 27, 26, 51, 52, 57, 56),
(22, 23, 28, 27, 52, 53, 58, 57),
(23, 24, 29, 28, 53, 54, 59, 58),
(24, 25, 30, 29, 54, 55, 60, 59),
(31, 32, 37, 36, 61, 62, 67, 66),
(36, 37, 42, 41, 66, 67, 72, 71),
(41, 42, 47, 46, 71, 72, 77, 76),
(42, 43, 48, 47, 72, 73, 78, 77),
(43, 44, 49, 48, 73, 74, 79, 78),
(44, 45, 50, 49, 74, 75, 80, 79),
(46, 47, 52, 51, 76, 77, 82, 81),
(51, 52, 57, 56, 81, 82, 87, 86),
(52, 53, 58, 57, 82, 83, 88, 87),
(53, 54, 59, 58, 83, 84, 89, 88),
(54, 55, 60, 59, 84, 85, 90, 89),
(61, 62, 67, 66, 91, 92, 97, 96),
(66, 67, 72, 71, 96, 97, 102, 101),
(71, 72, 77, 76, 101, 102, 107, 106),
(76, 77, 82, 81, 106, 107, 112, 111),
(81, 82, 87, 86, 111, 112, 117, 116),
(82, 83, 88, 87, 112, 113, 118, 117),
(83, 84, 89, 88, 113, 114, 119, 118),
(84, 85, 90, 89, 114, 115, 120, 119),
),
)
gold_mesh_element_connectivity = (
(
1,
(1, 2, 7, 6, 31, 32, 37, 36),
(2, 3, 8, 7, 32, 33, 38, 37),
(3, 4, 9, 8, 33, 34, 39, 38),
(4, 5, 10, 9, 34, 35, 40, 39),
(6, 7, 12, 11, 36, 37, 42, 41),
(7, 8, 13, 12, 37, 38, 43, 42),
(8, 9, 14, 13, 38, 39, 44, 43),
(9, 10, 15, 14, 39, 40, 45, 44),
(11, 12, 17, 16, 41, 42, 47, 46),
(12, 13, 18, 17, 42, 43, 48, 47),
(13, 14, 19, 18, 43, 44, 49, 48),
(14, 15, 20, 19, 44, 45, 50, 49),
(16, 17, 22, 21, 46, 47, 52, 51),
(17, 18, 23, 22, 47, 48, 53, 52),
(18, 19, 24, 23, 48, 49, 54, 53),
(19, 20, 25, 24, 49, 50, 55, 54),
(21, 22, 27, 26, 51, 52, 57, 56),
(22, 23, 28, 27, 52, 53, 58, 57),
(23, 24, 29, 28, 53, 54, 59, 58),
(24, 25, 30, 29, 54, 55, 60, 59),
(31, 32, 37, 36, 61, 62, 64, 63),
(36, 37, 42, 41, 63, 64, 66, 65),
(41, 42, 47, 46, 65, 66, 71, 70),
(42, 43, 48, 47, 66, 67, 72, 71),
(43, 44, 49, 48, 67, 68, 73, 72),
(44, 45, 50, 49, 68, 69, 74, 73),
(46, 47, 52, 51, 70, 71, 76, 75),
(51, 52, 57, 56, 75, 76, 81, 80),
(52, 53, 58, 57, 76, 77, 82, 81),
(53, 54, 59, 58, 77, 78, 83, 82),
(54, 55, 60, 59, 78, 79, 84, 83),
(61, 62, 64, 63, 85, 86, 88, 87),
(63, 64, 66, 65, 87, 88, 90, 89),
(65, 66, 71, 70, 89, 90, 92, 91),
(70, 71, 76, 75, 91, 92, 94, 93),
(75, 76, 81, 80, 93, 94, 99, 98),
(76, 77, 82, 81, 94, 95, 100, 99),
(77, 78, 83, 82, 95, 96, 101, 100),
(78, 79, 84, 83, 96, 97, 102, 101),
),
)
class Sparse(Example):
"""A radomized 5x5x5 segmentation."""
figure_title: str = COMMON_TITLE + "Sparse"
file_stem: str = "sparse"
segmentation = np.array(
[
[
[0, 0, 0, 0, 2],
[0, 1, 0, 0, 2],
[1, 2, 0, 2, 0],
[0, 1, 0, 2, 0],
[1, 0, 0, 0, 1],
],
[
[2, 0, 2, 0, 0],
[1, 1, 0, 2, 2],
[2, 0, 0, 0, 0],
[1, 0, 0, 2, 0],
[2, 0, 2, 0, 2],
],
[
[0, 0, 1, 0, 2],
[0, 0, 0, 1, 2],
[0, 0, 2, 2, 2],
[0, 0, 1, 0, 1],
[0, 1, 0, 1, 0],
],
[
[0, 1, 2, 1, 2],
[2, 0, 2, 0, 1],
[1, 2, 2, 0, 0],
[2, 1, 1, 1, 1],
[0, 0, 1, 0, 0],
],
[
[0, 1, 0, 2, 0],
[1, 0, 0, 0, 2],
[0, 1, 0, 0, 0],
[1, 0, 0, 0, 0],
[0, 0, 1, 2, 1],
],
],
dtype=np.uint8,
)
included_ids = (
1,
2,
)
gold_lattice = (
(1, 2, 8, 7, 37, 38, 44, 43),
(2, 3, 9, 8, 38, 39, 45, 44),
(3, 4, 10, 9, 39, 40, 46, 45),
(4, 5, 11, 10, 40, 41, 47, 46),
(5, 6, 12, 11, 41, 42, 48, 47),
(7, 8, 14, 13, 43, 44, 50, 49),
(8, 9, 15, 14, 44, 45, 51, 50),
(9, 10, 16, 15, 45, 46, 52, 51),
(10, 11, 17, 16, 46, 47, 53, 52),
(11, 12, 18, 17, 47, 48, 54, 53),
(13, 14, 20, 19, 49, 50, 56, 55),
(14, 15, 21, 20, 50, 51, 57, 56),
(15, 16, 22, 21, 51, 52, 58, 57),
(16, 17, 23, 22, 52, 53, 59, 58),
(17, 18, 24, 23, 53, 54, 60, 59),
(19, 20, 26, 25, 55, 56, 62, 61),
(20, 21, 27, 26, 56, 57, 63, 62),
(21, 22, 28, 27, 57, 58, 64, 63),
(22, 23, 29, 28, 58, 59, 65, 64),
(23, 24, 30, 29, 59, 60, 66, 65),
(25, 26, 32, 31, 61, 62, 68, 67),
(26, 27, 33, 32, 62, 63, 69, 68),
(27, 28, 34, 33, 63, 64, 70, 69),
(28, 29, 35, 34, 64, 65, 71, 70),
(29, 30, 36, 35, 65, 66, 72, 71),
(37, 38, 44, 43, 73, 74, 80, 79),
(38, 39, 45, 44, 74, 75, 81, 80),
(39, 40, 46, 45, 75, 76, 82, 81),
(40, 41, 47, 46, 76, 77, 83, 82),
(41, 42, 48, 47, 77, 78, 84, 83),
(43, 44, 50, 49, 79, 80, 86, 85),
(44, 45, 51, 50, 80, 81, 87, 86),
(45, 46, 52, 51, 81, 82, 88, 87),
(46, 47, 53, 52, 82, 83, 89, 88),
(47, 48, 54, 53, 83, 84, 90, 89),
(49, 50, 56, 55, 85, 86, 92, 91),
(50, 51, 57, 56, 86, 87, 93, 92),
(51, 52, 58, 57, 87, 88, 94, 93),
(52, 53, 59, 58, 88, 89, 95, 94),
(53, 54, 60, 59, 89, 90, 96, 95),
(55, 56, 62, 61, 91, 92, 98, 97),
(56, 57, 63, 62, 92, 93, 99, 98),
(57, 58, 64, 63, 93, 94, 100, 99),
(58, 59, 65, 64, 94, 95, 101, 100),
(59, 60, 66, 65, 95, 96, 102, 101),
(61, 62, 68, 67, 97, 98, 104, 103),
(62, 63, 69, 68, 98, 99, 105, 104),
(63, 64, 70, 69, 99, 100, 106, 105),
(64, 65, 71, 70, 100, 101, 107, 106),
(65, 66, 72, 71, 101, 102, 108, 107),
(73, 74, 80, 79, 109, 110, 116, 115),
(74, 75, 81, 80, 110, 111, 117, 116),
(75, 76, 82, 81, 111, 112, 118, 117),
(76, 77, 83, 82, 112, 113, 119, 118),
(77, 78, 84, 83, 113, 114, 120, 119),
(79, 80, 86, 85, 115, 116, 122, 121),
(80, 81, 87, 86, 116, 117, 123, 122),
(81, 82, 88, 87, 117, 118, 124, 123),
(82, 83, 89, 88, 118, 119, 125, 124),
(83, 84, 90, 89, 119, 120, 126, 125),
(85, 86, 92, 91, 121, 122, 128, 127),
(86, 87, 93, 92, 122, 123, 129, 128),
(87, 88, 94, 93, 123, 124, 130, 129),
(88, 89, 95, 94, 124, 125, 131, 130),
(89, 90, 96, 95, 125, 126, 132, 131),
(91, 92, 98, 97, 127, 128, 134, 133),
(92, 93, 99, 98, 128, 129, 135, 134),
(93, 94, 100, 99, 129, 130, 136, 135),
(94, 95, 101, 100, 130, 131, 137, 136),
(95, 96, 102, 101, 131, 132, 138, 137),
(97, 98, 104, 103, 133, 134, 140, 139),
(98, 99, 105, 104, 134, 135, 141, 140),
(99, 100, 106, 105, 135, 136, 142, 141),
(100, 101, 107, 106, 136, 137, 143, 142),
(101, 102, 108, 107, 137, 138, 144, 143),
(109, 110, 116, 115, 145, 146, 152, 151),
(110, 111, 117, 116, 146, 147, 153, 152),
(111, 112, 118, 117, 147, 148, 154, 153),
(112, 113, 119, 118, 148, 149, 155, 154),
(113, 114, 120, 119, 149, 150, 156, 155),
(115, 116, 122, 121, 151, 152, 158, 157),
(116, 117, 123, 122, 152, 153, 159, 158),
(117, 118, 124, 123, 153, 154, 160, 159),
(118, 119, 125, 124, 154, 155, 161, 160),
(119, 120, 126, 125, 155, 156, 162, 161),
(121, 122, 128, 127, 157, 158, 164, 163),
(122, 123, 129, 128, 158, 159, 165, 164),
(123, 124, 130, 129, 159, 160, 166, 165),
(124, 125, 131, 130, 160, 161, 167, 166),
(125, 126, 132, 131, 161, 162, 168, 167),
(127, 128, 134, 133, 163, 164, 170, 169),
(128, 129, 135, 134, 164, 165, 171, 170),
(129, 130, 136, 135, 165, 166, 172, 171),
(130, 131, 137, 136, 166, 167, 173, 172),
(131, 132, 138, 137, 167, 168, 174, 173),
(133, 134, 140, 139, 169, 170, 176, 175),
(134, 135, 141, 140, 170, 171, 177, 176),
(135, 136, 142, 141, 171, 172, 178, 177),
(136, 137, 143, 142, 172, 173, 179, 178),
(137, 138, 144, 143, 173, 174, 180, 179),
(145, 146, 152, 151, 181, 182, 188, 187),
(146, 147, 153, 152, 182, 183, 189, 188),
(147, 148, 154, 153, 183, 184, 190, 189),
(148, 149, 155, 154, 184, 185, 191, 190),
(149, 150, 156, 155, 185, 186, 192, 191),
(151, 152, 158, 157, 187, 188, 194, 193),
(152, 153, 159, 158, 188, 189, 195, 194),
(153, 154, 160, 159, 189, 190, 196, 195),
(154, 155, 161, 160, 190, 191, 197, 196),
(155, 156, 162, 161, 191, 192, 198, 197),
(157, 158, 164, 163, 193, 194, 200, 199),
(158, 159, 165, 164, 194, 195, 201, 200),
(159, 160, 166, 165, 195, 196, 202, 201),
(160, 161, 167, 166, 196, 197, 203, 202),
(161, 162, 168, 167, 197, 198, 204, 203),
(163, 164, 170, 169, 199, 200, 206, 205),
(164, 165, 171, 170, 200, 201, 207, 206),
(165, 166, 172, 171, 201, 202, 208, 207),
(166, 167, 173, 172, 202, 203, 209, 208),
(167, 168, 174, 173, 203, 204, 210, 209),
(169, 170, 176, 175, 205, 206, 212, 211),
(170, 171, 177, 176, 206, 207, 213, 212),
(171, 172, 178, 177, 207, 208, 214, 213),
(172, 173, 179, 178, 208, 209, 215, 214),
(173, 174, 180, 179, 209, 210, 216, 215),
)
gold_mesh_lattice_connectivity = (
(
1,
(8, 9, 15, 14, 44, 45, 51, 50),
(13, 14, 20, 19, 49, 50, 56, 55),
(20, 21, 27, 26, 56, 57, 63, 62),
(25, 26, 32, 31, 61, 62, 68, 67),
(29, 30, 36, 35, 65, 66, 72, 71),
(43, 44, 50, 49, 79, 80, 86, 85),
(44, 45, 51, 50, 80, 81, 87, 86),
(55, 56, 62, 61, 91, 92, 98, 97),
(75, 76, 82, 81, 111, 112, 118, 117),
(82, 83, 89, 88, 118, 119, 125, 124),
(93, 94, 100, 99, 129, 130, 136, 135),
(95, 96, 102, 101, 131, 132, 138, 137),
(98, 99, 105, 104, 134, 135, 141, 140),
(100, 101, 107, 106, 136, 137, 143, 142),
(110, 111, 117, 116, 146, 147, 153, 152),
(112, 113, 119, 118, 148, 149, 155, 154),
(119, 120, 126, 125, 155, 156, 162, 161),
(121, 122, 128, 127, 157, 158, 164, 163),
(128, 129, 135, 134, 164, 165, 171, 170),
(129, 130, 136, 135, 165, 166, 172, 171),
(130, 131, 137, 136, 166, 167, 173, 172),
(131, 132, 138, 137, 167, 168, 174, 173),
(135, 136, 142, 141, 171, 172, 178, 177),
(146, 147, 153, 152, 182, 183, 189, 188),
(151, 152, 158, 157, 187, 188, 194, 193),
(158, 159, 165, 164, 194, 195, 201, 200),
(163, 164, 170, 169, 199, 200, 206, 205),
(171, 172, 178, 177, 207, 208, 214, 213),
(173, 174, 180, 179, 209, 210, 216, 215),
),
(
2,
(5, 6, 12, 11, 41, 42, 48, 47),
(11, 12, 18, 17, 47, 48, 54, 53),
(14, 15, 21, 20, 50, 51, 57, 56),
(16, 17, 23, 22, 52, 53, 59, 58),
(22, 23, 29, 28, 58, 59, 65, 64),
(37, 38, 44, 43, 73, 74, 80, 79),
(39, 40, 46, 45, 75, 76, 82, 81),
(46, 47, 53, 52, 82, 83, 89, 88),
(47, 48, 54, 53, 83, 84, 90, 89),
(49, 50, 56, 55, 85, 86, 92, 91),
(58, 59, 65, 64, 94, 95, 101, 100),
(61, 62, 68, 67, 97, 98, 104, 103),
(63, 64, 70, 69, 99, 100, 106, 105),
(65, 66, 72, 71, 101, 102, 108, 107),
(77, 78, 84, 83, 113, 114, 120, 119),
(83, 84, 90, 89, 119, 120, 126, 125),
(87, 88, 94, 93, 123, 124, 130, 129),
(88, 89, 95, 94, 124, 125, 131, 130),
(89, 90, 96, 95, 125, 126, 132, 131),
(111, 112, 118, 117, 147, 148, 154, 153),
(113, 114, 120, 119, 149, 150, 156, 155),
(115, 116, 122, 121, 151, 152, 158, 157),
(117, 118, 124, 123, 153, 154, 160, 159),
(122, 123, 129, 128, 158, 159, 165, 164),
(123, 124, 130, 129, 159, 160, 166, 165),
(127, 128, 134, 133, 163, 164, 170, 169),
(148, 149, 155, 154, 184, 185, 191, 190),
(155, 156, 162, 161, 191, 192, 198, 197),
(172, 173, 179, 178, 208, 209, 215, 214),
),
)
gold_mesh_element_connectivity = (
(
1,
(3, 4, 9, 8, 35, 36, 42, 41),
(7, 8, 14, 13, 40, 41, 47, 46),
(14, 15, 20, 19, 47, 48, 53, 52),
(18, 19, 25, 24, 51, 52, 58, 57),
(22, 23, 27, 26, 55, 56, 62, 61),
(34, 35, 41, 40, 69, 70, 76, 75),
(35, 36, 42, 41, 70, 71, 77, 76),
(46, 47, 52, 51, 81, 82, 88, 87),
(65, 66, 72, 71, 100, 101, 107, 106),
(72, 73, 79, 78, 107, 108, 114, 113),
(83, 84, 90, 89, 118, 119, 125, 124),
(85, 86, 92, 91, 120, 121, 127, 126),
(88, 89, 95, 94, 123, 124, 129, 128),
(90, 91, 97, 96, 125, 126, 131, 130),
(99, 100, 106, 105, 132, 133, 139, 138),
(101, 102, 108, 107, 134, 135, 141, 140),
(108, 109, 115, 114, 141, 142, 148, 147),
(110, 111, 117, 116, 143, 144, 150, 149),
(117, 118, 124, 123, 150, 151, 157, 156),
(118, 119, 125, 124, 151, 152, 158, 157),
(119, 120, 126, 125, 152, 153, 159, 158),
(120, 121, 127, 126, 153, 154, 160, 159),
(124, 125, 130, 129, 157, 158, 162, 161),
(132, 133, 139, 138, 165, 166, 171, 170),
(137, 138, 144, 143, 169, 170, 176, 175),
(144, 145, 151, 150, 176, 177, 182, 181),
(149, 150, 156, 155, 180, 181, 184, 183),
(157, 158, 162, 161, 185, 186, 190, 189),
(159, 160, 164, 163, 187, 188, 192, 191),
),
(
2,
(1, 2, 6, 5, 32, 33, 39, 38),
(5, 6, 12, 11, 38, 39, 45, 44),
(8, 9, 15, 14, 41, 42, 48, 47),
(10, 11, 17, 16, 43, 44, 50, 49),
(16, 17, 22, 21, 49, 50, 55, 54),
(28, 29, 35, 34, 63, 64, 70, 69),
(30, 31, 37, 36, 65, 66, 72, 71),
(37, 38, 44, 43, 72, 73, 79, 78),
(38, 39, 45, 44, 73, 74, 80, 79),
(40, 41, 47, 46, 75, 76, 82, 81),
(49, 50, 55, 54, 84, 85, 91, 90),
(51, 52, 58, 57, 87, 88, 94, 93),
(53, 54, 60, 59, 89, 90, 96, 95),
(55, 56, 62, 61, 91, 92, 98, 97),
(67, 68, 74, 73, 102, 103, 109, 108),
(73, 74, 80, 79, 108, 109, 115, 114),
(77, 78, 84, 83, 112, 113, 119, 118),
(78, 79, 85, 84, 113, 114, 120, 119),
(79, 80, 86, 85, 114, 115, 121, 120),
(100, 101, 107, 106, 133, 134, 140, 139),
(102, 103, 109, 108, 135, 136, 142, 141),
(104, 105, 111, 110, 137, 138, 144, 143),
(106, 107, 113, 112, 139, 140, 146, 145),
(111, 112, 118, 117, 144, 145, 151, 150),
(112, 113, 119, 118, 145, 146, 152, 151),
(116, 117, 123, 122, 149, 150, 156, 155),
(134, 135, 141, 140, 167, 168, 173, 172),
(141, 142, 148, 147, 173, 174, 179, 178),
(158, 159, 163, 162, 186, 187, 191, 190),
),
)
examples_figures.py
r"""This module, examples_figures.py, demonstrates creating a pixel slice in
the (x, y) plane, and then appending layers in the z axis, to create a 3D
voxel lattice, as a precursor for a hexahedral finite element mesh.
Example
-------
source ~/autotwin/automesh/.venv/bin/activate
pip install matplotlib
cd ~/autotwin/automesh/book/examples/unit_tests
python examples_figures.py
Ouputk
-----
The `output_npy` segmentation data files
The `output_png` visualization files
"""
# standard library
import datetime
from pathlib import Path
from typing import Final
# third-party libary
import matplotlib.pyplot as plt
from matplotlib.colors import LightSource
import numpy as np
from numpy.typing import NDArray
import examples_types as types
import examples_data as data
# Type aliases
Example = types.Example
def lattice_connectivity(ex: Example) -> NDArray[np.uint8]:
"""Given an Example, prints the lattice connectivity."""
offset = 0
nz, ny, nx = ex.segmentation.shape
nzp, nyp, nxp = nz + 1, ny + 1, nx + 1
# Generate the lattice nodes
lattice_nodes = []
lattice_node = 0
for k in range(nzp):
for j in range(nyp):
for i in range(nxp):
lattice_node += 1
lattice_nodes.append([lattice_node, i, j, k])
# connectivity for each voxel
cvs = []
offset = 0
# print("processing indices...")
for iz in range(nz):
for iy in range(ny):
for ix in range(nx):
# print(f"(ix, iy, iz) = ({ix}, {iy}, {iz})")
cv = offset + np.array(
[
(iz + 0) * (nxp * nyp) + (iy + 0) * nxp + ix + 1,
(iz + 0) * (nxp * nyp) + (iy + 0) * nxp + ix + 2,
(iz + 0) * (nxp * nyp) + (iy + 1) * nxp + ix + 2,
(iz + 0) * (nxp * nyp) + (iy + 1) * nxp + ix + 1,
(iz + 1) * (nxp * nyp) + (iy + 0) * nxp + ix + 1,
(iz + 1) * (nxp * nyp) + (iy + 0) * nxp + ix + 2,
(iz + 1) * (nxp * nyp) + (iy + 1) * nxp + ix + 2,
(iz + 1) * (nxp * nyp) + (iy + 1) * nxp + ix + 1,
]
)
cvs.append(cv)
cs = np.vstack(cvs)
# voxel by voxel comparison
# breakpoint()
vv = ex.gold_lattice == cs
assert np.all(vv)
return cs
def mesh_lattice_connectivity(
ex: Example,
lattice: np.ndarray,
) -> tuple:
"""Given an Example (in particular, the Example's voxel data structure,
a segmentation) and the `lattice_connectivity`, create the connectivity
for the mesh with lattice node numbers. A voxel with a segmentation id not
in the Example's included ids tuple is excluded from the mesh.
"""
# segmentation = ex.segmentation.flatten().squeeze()
segmentation = ex.segmentation.flatten()
# breakpoint()
# assert that the list of included ids is equal
included_set_unordered = set(ex.included_ids)
included_list_ordered = sorted(included_set_unordered)
# breakpoint()
seg_set = set(segmentation)
for item in included_list_ordered:
assert item in seg_set, (
f"Error: `included_ids` item {item} is not in the segmentation"
)
# Create a list of finite elements from the lattice elements. If the
# lattice element has a segmentation id that is not in the included_ids,
# exlude the voxel element from the collected list to create the finite
# element list
blocks = () # empty tuple
# breakpoint()
for bb in included_list_ordered:
# included_elements = []
elements = () # empty tuple
elements = elements + (bb,) # insert the block number
for i, element in enumerate(lattice):
if bb == segmentation[i]:
# breakpoint()
elements = elements + (tuple(element.tolist()),) # overwrite
blocks = blocks + (elements,) # overwrite
# breakpoint()
# return np.array(blocks)
return blocks
def renumber(source: tuple, old: tuple, new: tuple) -> tuple:
"""Given a source tuple, composed of a list of positive integers,
a tuple of `old` numbers that maps into `new` numbers, return the
source tuple with the `new` numbers."""
# the old and the new tuples musts have the same length
err = "Tuples `old` and `new` must have equal length."
assert len(old) == len(new), err
result = ()
for item in source:
idx = old.index(item)
new_value = new[idx]
result = result + (new_value,)
return result
def mesh_element_connectivity(mesh_with_lattice_connectivity: tuple):
"""Given a mesh with lattice connectivity, return a mesh with finite
element connectivity.
"""
# create a list of unordered lattice node numbers
ln = []
for item in mesh_with_lattice_connectivity:
# print(f"item is {item}")
# The first item is the block number
# block = item[0]
# The second and onward items are the elements
elements = item[1:]
for element in elements:
ln += list(element)
ln_set = set(ln) # sets are not necessarily ordered
ln_ordered = tuple(sorted(ln_set)) # now these unique integers are ordered
# and they will map into the new compressed unique interger list `mapsto`
mapsto = tuple(range(1, len(ln_ordered) + 1))
# now build a mesh_with_element_connectivity
mesh = () # empty tuple
# breakpoint()
for item in mesh_with_lattice_connectivity:
# The first item is the block number
block_number = item[0]
block_and_elements = () # empty tuple
# insert the block number
block_and_elements = block_and_elements + (block_number,)
for element in item[1:]:
new_element = renumber(source=element, old=ln_ordered, new=mapsto)
# overwrite
block_and_elements = block_and_elements + (new_element,)
mesh = mesh + (block_and_elements,) # overwrite
return mesh
def flatten_tuple(t):
"""Uses recursion to convert nested tuples into a single-sevel tuple.
Example:
nested_tuple = (1, (2, 3), (4, (5, 6)), 7)
flattened_tuple = flatten_tuple(nested_tuple)
print(flattened_tuple) # Output: (1, 2, 3, 4, 5, 6, 7)
"""
flat_list = []
for item in t:
if isinstance(item, tuple):
flat_list.extend(flatten_tuple(item))
else:
flat_list.append(item)
# breakpoint()
return tuple(flat_list)
def elements_without_block_ids(mesh: tuple) -> tuple:
"""Given a mesh, removes the block ids and returns only just the
element connectivities.
"""
aa = ()
for item in mesh:
bb = item[1:]
aa = aa + bb
return aa
def main():
"""The main program."""
# Create an instance of a specific example
# user input begin
examples = [
data.Single(),
# data.DoubleX(),
# data.DoubleY(),
# data.TripleX(),
# data.QuadrupleX(),
# data.Quadruple2VoidsX(),
# data.Quadruple2Blocks(),
# data.Quadruple2BlocksVoid(),
# data.Cube(),
# data.CubeMulti(),
# data.CubeWithInclusion(),
data.Bracket(),
# data.LetterF(),
# data.LetterF3D(),
# data.Sparse(),
]
# output_dir: Final[str] = "~/scratch"
output_dir: Final[Path] = Path(__file__).parent
DPI: Final[int] = 300 # resolution, dots per inch
for ex in examples:
# computation
output_npy: Path = Path(output_dir).expanduser().joinpath(ex.file_stem + ".npy")
# visualization
SHOW: Final[bool] = True # Post-processing visuals, show on screen
SAVE: Final[bool] = True # Save the .png file
output_png_short = ex.file_stem + ".png"
output_png: Path = Path(output_dir).expanduser().joinpath(output_png_short)
# el, az, roll = 25, -115, 0
# el, az, roll = 28, -115, 0
el, az, roll = 63, -110, 0 # used for most visuals
# el, az, roll = 11, -111, 0 # used for CubeWithInclusion
# el, az, roll = 60, -121, 0
# el, az, roll = 42, -120, 0
#
# colors
# cmap = cm.get_cmap("viridis") # viridis colormap
# cmap = plt.get_cmap(name="viridis")
cmap = plt.get_cmap(name="tab10")
# number of discrete colors
num_colors = len(ex.included_ids)
colors = cmap(np.linspace(0, 1, num_colors))
# breakpoint()
# azimuth (deg):
# 0 is east (from +y-axis looking back toward origin)
# 90 is north (from +x-axis looking back toward origin)
# 180 is west (from -y-axis looking back toward origin)
# 270 is south (from -x-axis looking back toward origin)
# elevation (deg): 0 is horizontal, 90 is vertical (+z-axis up)
lightsource = LightSource(azdeg=325, altdeg=45) # azimuth, elevation
nodes_shown: bool = True
# nodes_shown: bool = False
voxel_alpha: float = 0.1
# voxel_alpha: float = 0.7
# io: if the output directory does not already exist, create it
output_path = Path(output_dir).expanduser()
if not output_path.exists():
print(f"Could not find existing output directory: {output_path}")
Path.mkdir(output_path)
print(f"Created: {output_path}")
assert output_path.exists()
nelz, nely, nelx = ex.segmentation.shape
lc = lattice_connectivity(ex=ex)
# breakpoint()
mesh_w_lattice_conn = mesh_lattice_connectivity(ex=ex, lattice=lc)
err = "Calculated lattice connectivity error."
assert mesh_w_lattice_conn == ex.gold_mesh_lattice_connectivity, err
mesh_w_element_conn = mesh_element_connectivity(mesh_w_lattice_conn)
err = "Calcualted element connectivity error." # overwrite
assert mesh_w_element_conn == ex.gold_mesh_element_connectivity, err
# save the numpy data as a .npy file
np.save(output_npy, ex.segmentation)
print(f"Saved: {output_npy}")
# to load the array back from the .npy file,
# use the numpy.load function:
loaded_array = np.load(output_npy)
# verify the loaded array
# print(f"segmentation loaded from saved file: {loaded_array}")
assert np.all(loaded_array == ex.segmentation)
# now that the .npy file has been created and verified,
# move it to the repo at ~/autotwin/automesh/tests/input
if not SHOW:
return
# visualization
# Define the dimensions of the lattice
nxp, nyp, nzp = (nelx + 1, nely + 1, nelz + 1)
# Create a figure and a 3D axis
# fig = plt.figure()
fig = plt.figure(figsize=(10, 5)) # Adjust the figure size
# fig = plt.figure(figsize=(8, 4)) # Adjust the figure size
# ax = fig.add_subplot(111, projection="3d")
# figure with 1 row, 2 columns
ax = fig.add_subplot(1, 2, 1, projection="3d") # r1, c2, 1st subplot
ax2 = fig.add_subplot(1, 2, 2, projection="3d") # r1, c2, 2nd subplot
# For 3D plotting of voxels in matplotlib, we must swap the 'x' and the
# 'z' axes. The original axes in the segmentation are (z, y, x) and
# are numbered (0, 1, 2). We want new exists as (x, y, z) and thus
# with numbering (2, 1, 0).
vox = np.transpose(ex.segmentation, (2, 1, 0))
# add voxels for each of the included materials
for i, block_id in enumerate(ex.included_ids):
# breakpoint()
solid = vox == block_id
# ax.voxels(solid, facecolors=voxel_color, alpha=voxel_alpha)
# ax.voxels(solid, facecolors=colors[i], alpha=voxel_alpha)
ax.voxels(
solid,
facecolors=colors[i],
edgecolor=colors[i],
alpha=voxel_alpha,
lightsource=lightsource,
)
# plot the same voxels on the 2nd axis
ax2.voxels(
solid,
facecolors=colors[i],
edgecolor=colors[i],
alpha=voxel_alpha,
lightsource=lightsource,
)
# breakpoint()
# Generate the lattice points
x = []
y = []
z = []
labels = []
# Generate the element points
xel = []
yel = []
zel = []
# generate a set from the element connectivity
# breakpoint()
# ec_set = set(flatten_tuple(mesh_w_lattice_conn)) # bug!
# bug fix:
ec_set = set(flatten_tuple(elements_without_block_ids(mesh_w_lattice_conn)))
# breakpoint()
lattice_ijk = 0
# gnn = global node number
gnn = 0
gnn_labels = []
for k in range(nzp):
for j in range(nyp):
for i in range(nxp):
x.append(i)
y.append(j)
z.append(k)
if lattice_ijk + 1 in ec_set:
gnn += 1
xel.append(i)
yel.append(j)
zel.append(k)
gnn_labels.append(f" {gnn}")
lattice_ijk += 1
labels.append(f" {lattice_ijk}: ({i},{j},{k})")
if nodes_shown:
# Plot the lattice coordinates
ax.scatter(
x,
y,
z,
s=20,
facecolors="red",
edgecolors="none",
)
# Label the lattice coordinates
for n, label in enumerate(labels):
ax.text(x[n], y[n], z[n], label, color="darkgray", fontsize=8)
# Plot the nodes included in the finite element connectivity
ax2.scatter(
xel,
yel,
zel,
s=30,
facecolors="blue",
edgecolors="blue",
)
# Label the global node numbers
for n, label in enumerate(gnn_labels):
ax2.text(xel[n], yel[n], zel[n], label, color="darkblue", fontsize=8)
# Set labels for the axes
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("z")
# repeat for the 2nd axis
ax2.set_xlabel("x")
ax2.set_ylabel("y")
ax2.set_zlabel("z")
x_ticks = list(range(nxp))
y_ticks = list(range(nyp))
z_ticks = list(range(nzp))
ax.set_xticks(x_ticks)
ax.set_yticks(y_ticks)
ax.set_zticks(z_ticks)
# repeat for the 2nd axis
ax2.set_xticks(x_ticks)
ax2.set_yticks(y_ticks)
ax2.set_zticks(z_ticks)
ax.set_xlim(float(x_ticks[0]), float(x_ticks[-1]))
ax.set_ylim(float(y_ticks[0]), float(y_ticks[-1]))
ax.set_zlim(float(z_ticks[0]), float(z_ticks[-1]))
# repeat for the 2nd axis
ax2.set_xlim(float(x_ticks[0]), float(x_ticks[-1]))
ax2.set_ylim(float(y_ticks[0]), float(y_ticks[-1]))
ax2.set_zlim(float(z_ticks[0]), float(z_ticks[-1]))
# Set the camera view
ax.set_aspect("equal")
ax.view_init(elev=el, azim=az, roll=roll)
# repeat for the 2nd axis
ax2.set_aspect("equal")
ax2.view_init(elev=el, azim=az, roll=roll)
# Adjust the distance of the camera. The default value is 10.
# Increasing/decreasing this value will zoom in/out, respectively.
# ax.dist = 5 # Change the distance of the camera
# Doesn't seem to work, and the title is clipping the uppermost node
# and lattice numbers, so suppress the titles for now.
# Set the title
# ax.set_title(ex.figure_title)
# Add a footnote
# Get the current date and time in UTC
now_utc = datetime.datetime.now(datetime.UTC)
# Format the date and time as a string
timestamp_utc = now_utc.strftime("%Y-%m-%d %H:%M:%S UTC")
fn = f"Figure: {output_png_short} "
fn += f"created with {__file__}\non {timestamp_utc}."
fig.text(0.5, 0.01, fn, ha="center", fontsize=8)
# Show the plot
if SHOW:
plt.show()
if SAVE:
# plt.show()
fig.savefig(output_png, dpi=DPI)
print(f"Saved: {output_png}")
if __name__ == "__main__":
main()
examples_test.py
r"""This module, examples_test.py, tests functionality of the included module.
Example
-------
source ~/autotwin/automesh/.venv/bin/activate
cd ~/autotwin/automesh/book/examples/unit_tests
python -m pytest examples_test.py -v # -v is for verbose
to run a single test in this module, for example `test_hello` function:
python -m pytest examples_test.py::test_foo -v
"""
import pytest
import examples_figures as ff
def test_renumber():
"""Tests that the renumber function works as expected."""
source = (300, 22, 1)
old = (1, 22, 300, 40)
new = (42, 2, 9, 1000)
result = ff.renumber(source=source, old=old, new=new)
assert result == (9, 2, 42)
# Assure that tuples old and new of unequal length raise an AssertionError
new = (42, 2) # overwrite
err = "Tuples `old` and `new` must have equal length."
with pytest.raises(AssertionError, match=err):
_ = ff.renumber(source=source, old=old, new=new)
def test_mesh_with_element_connectivity():
"""Test CubeMulti by hand."""
gold_mesh_lattice_connectivity = (
(
2,
(2, 3, 6, 5, 11, 12, 15, 14),
(4, 5, 8, 7, 13, 14, 17, 16),
(5, 6, 9, 8, 14, 15, 18, 17),
),
(
31,
(11, 12, 15, 14, 20, 21, 24, 23),
),
(
44,
(14, 15, 18, 17, 23, 24, 27, 26),
),
(
82,
(1, 2, 5, 4, 10, 11, 14, 13),
),
)
gold_mesh_element_connectivity = (
(
2,
(2, 3, 6, 5, 11, 12, 15, 14),
(4, 5, 8, 7, 13, 14, 17, 16),
(5, 6, 9, 8, 14, 15, 18, 17),
),
(31, (11, 12, 15, 14, 19, 20, 22, 21)),
(44, (14, 15, 18, 17, 21, 22, 24, 23)),
(82, (1, 2, 5, 4, 10, 11, 14, 13)),
)
result = ff.mesh_element_connectivity(
mesh_with_lattice_connectivity=gold_mesh_lattice_connectivity
)
assert result == gold_mesh_element_connectivity
def test_elements_no_block_ids():
"""Given a mesh, strips the block ids from the"""
known_input = (
(
2,
(2, 3, 6, 5, 11, 12, 15, 14),
(4, 5, 8, 7, 13, 14, 17, 16),
(5, 6, 9, 8, 14, 15, 18, 17),
),
(31, (11, 12, 15, 14, 20, 21, 24, 23)),
(44, (14, 15, 18, 17, 23, 24, 27, 26)),
(82, (1, 2, 5, 4, 10, 11, 14, 13)),
)
gold_output = (
(2, 3, 6, 5, 11, 12, 15, 14),
(4, 5, 8, 7, 13, 14, 17, 16),
(5, 6, 9, 8, 14, 15, 18, 17),
(11, 12, 15, 14, 20, 21, 24, 23),
(14, 15, 18, 17, 23, 24, 27, 26),
(1, 2, 5, 4, 10, 11, 14, 13),
)
result = ff.elements_without_block_ids(mesh=known_input)
assert result == gold_output
examples_types.py
r"""This module, examples_types.py, defines types used
for unit test examples.
"""
from typing import NamedTuple
import numpy as np
class Example(NamedTuple):
"""A base class that has all of the fields required to specialize into a
specific example."""
figure_title: str = "Figure Title"
file_stem: str = "filename"
segmentation = np.array(
[
[
[
1,
],
],
],
dtype=np.uint8,
)
included_ids = (1,)
gold_lattice = None
gold_mesh_lattice_connectivity = None
gold_mesh_element_connectivity = None
Spheres
We segment a sphere into very coarse voxel meshes. The Python code used to generate the voxelations and figures is included below.
Segmentation
Objective: Create very coarse spheres of three successively more refined
resolutions, radius=1, radius=3, and radius=5, as shown below:
Figure: Sphere segmentations at selected resolutions, shown in the voxel domain.
The radius=1 case has the following data structure,
spheres["radius_1"]
array([[[0, 0, 0],
[0, 1, 0],
[0, 0, 0]],
[[0, 1, 0],
[1, 1, 1],
[0, 1, 0]],
[[0, 0, 0],
[0, 1, 0],
[0, 0, 0]]], dtype=uint8)
Because of large size, the data structures for sphere_3 and
sphere_5 are not shown here.
These segmentations are saved to
automesh
automesh is used to convert the .npy segmentations into .inp meshes.
automesh mesh hex -i spheres_radius_1.npy -o spheres_radius_1.inp
automesh 0.3.8
Reading spheres_radius_1.npy
Done 65.689µs [2 materials, 27 voxels]
Meshing voxels into hexahedra
Done 260.492µs [2 blocks, 27 elements, 64 nodes]
Writing spheres_radius_1.inp
Done 94.553µs
Total 732.004µs
automesh mesh hex -i spheres_radius_3.npy -o spheres_radius_3.inp
automesh 0.3.8
Reading spheres_radius_3.npy
Done 66.965µs [2 materials, 343 voxels]
Meshing voxels into hexahedra
Done 293.006µs [2 blocks, 343 elements, 512 nodes]
Writing spheres_radius_3.inp
Done 564.61µs
Total 1.220219ms
automesh mesh hex -i spheres_radius_5.npy -o spheres_radius_5.inp
automesh 0.3.8
Reading spheres_radius_5.npy
Done 65.209µs [2 materials, 1331 voxels]
Meshing voxels into hexahedra
Done 446.647µs [2 blocks, 1331 elements, 1728 nodes]
Writing spheres_radius_5.inp
Done 1.950062ms
Total 2.792232ms
Mesh
The spheres_radius_1.inp file:
** autotwin.automesh
** version 0.3.8
** autogenerated on 2026-02-27 16:47:08.836471689 UTC
********************************** N O D E S **********************************
*NODE, NSET=ALLNODES
1, 0.000000e0, 0.000000e0, 0.000000e0
2, 1.000000e0, 0.000000e0, 0.000000e0
3, 2.000000e0, 0.000000e0, 0.000000e0
4, 3.000000e0, 0.000000e0, 0.000000e0
5, 0.000000e0, 1.000000e0, 0.000000e0
6, 1.000000e0, 1.000000e0, 0.000000e0
7, 2.000000e0, 1.000000e0, 0.000000e0
8, 3.000000e0, 1.000000e0, 0.000000e0
9, 0.000000e0, 2.000000e0, 0.000000e0
10, 1.000000e0, 2.000000e0, 0.000000e0
11, 2.000000e0, 2.000000e0, 0.000000e0
12, 3.000000e0, 2.000000e0, 0.000000e0
13, 0.000000e0, 3.000000e0, 0.000000e0
14, 1.000000e0, 3.000000e0, 0.000000e0
15, 2.000000e0, 3.000000e0, 0.000000e0
16, 3.000000e0, 3.000000e0, 0.000000e0
17, 0.000000e0, 0.000000e0, 1.000000e0
18, 1.000000e0, 0.000000e0, 1.000000e0
19, 2.000000e0, 0.000000e0, 1.000000e0
20, 3.000000e0, 0.000000e0, 1.000000e0
21, 0.000000e0, 1.000000e0, 1.000000e0
22, 1.000000e0, 1.000000e0, 1.000000e0
23, 2.000000e0, 1.000000e0, 1.000000e0
24, 3.000000e0, 1.000000e0, 1.000000e0
25, 0.000000e0, 2.000000e0, 1.000000e0
26, 1.000000e0, 2.000000e0, 1.000000e0
27, 2.000000e0, 2.000000e0, 1.000000e0
28, 3.000000e0, 2.000000e0, 1.000000e0
29, 0.000000e0, 3.000000e0, 1.000000e0
30, 1.000000e0, 3.000000e0, 1.000000e0
31, 2.000000e0, 3.000000e0, 1.000000e0
32, 3.000000e0, 3.000000e0, 1.000000e0
33, 0.000000e0, 0.000000e0, 2.000000e0
34, 1.000000e0, 0.000000e0, 2.000000e0
35, 2.000000e0, 0.000000e0, 2.000000e0
36, 3.000000e0, 0.000000e0, 2.000000e0
37, 0.000000e0, 1.000000e0, 2.000000e0
38, 1.000000e0, 1.000000e0, 2.000000e0
39, 2.000000e0, 1.000000e0, 2.000000e0
40, 3.000000e0, 1.000000e0, 2.000000e0
41, 0.000000e0, 2.000000e0, 2.000000e0
42, 1.000000e0, 2.000000e0, 2.000000e0
43, 2.000000e0, 2.000000e0, 2.000000e0
44, 3.000000e0, 2.000000e0, 2.000000e0
45, 0.000000e0, 3.000000e0, 2.000000e0
46, 1.000000e0, 3.000000e0, 2.000000e0
47, 2.000000e0, 3.000000e0, 2.000000e0
48, 3.000000e0, 3.000000e0, 2.000000e0
49, 0.000000e0, 0.000000e0, 3.000000e0
50, 1.000000e0, 0.000000e0, 3.000000e0
51, 2.000000e0, 0.000000e0, 3.000000e0
52, 3.000000e0, 0.000000e0, 3.000000e0
53, 0.000000e0, 1.000000e0, 3.000000e0
54, 1.000000e0, 1.000000e0, 3.000000e0
55, 2.000000e0, 1.000000e0, 3.000000e0
56, 3.000000e0, 1.000000e0, 3.000000e0
57, 0.000000e0, 2.000000e0, 3.000000e0
58, 1.000000e0, 2.000000e0, 3.000000e0
59, 2.000000e0, 2.000000e0, 3.000000e0
60, 3.000000e0, 2.000000e0, 3.000000e0
61, 0.000000e0, 3.000000e0, 3.000000e0
62, 1.000000e0, 3.000000e0, 3.000000e0
63, 2.000000e0, 3.000000e0, 3.000000e0
64, 3.000000e0, 3.000000e0, 3.000000e0
**
********************************** E L E M E N T S ****************************
*ELEMENT, TYPE=C3D8R, ELSET=EB0
1, 1, 2, 6, 5, 17, 18, 22, 21
2, 2, 3, 7, 6, 18, 19, 23, 22
3, 3, 4, 8, 7, 19, 20, 24, 23
4, 5, 6, 10, 9, 21, 22, 26, 25
6, 7, 8, 12, 11, 23, 24, 28, 27
7, 9, 10, 14, 13, 25, 26, 30, 29
8, 10, 11, 15, 14, 26, 27, 31, 30
9, 11, 12, 16, 15, 27, 28, 32, 31
10, 17, 18, 22, 21, 33, 34, 38, 37
12, 19, 20, 24, 23, 35, 36, 40, 39
16, 25, 26, 30, 29, 41, 42, 46, 45
18, 27, 28, 32, 31, 43, 44, 48, 47
19, 33, 34, 38, 37, 49, 50, 54, 53
20, 34, 35, 39, 38, 50, 51, 55, 54
21, 35, 36, 40, 39, 51, 52, 56, 55
22, 37, 38, 42, 41, 53, 54, 58, 57
24, 39, 40, 44, 43, 55, 56, 60, 59
25, 41, 42, 46, 45, 57, 58, 62, 61
26, 42, 43, 47, 46, 58, 59, 63, 62
27, 43, 44, 48, 47, 59, 60, 64, 63
*ELEMENT, TYPE=C3D8R, ELSET=EB1
5, 6, 7, 11, 10, 22, 23, 27, 26
11, 18, 19, 23, 22, 34, 35, 39, 38
13, 21, 22, 26, 25, 37, 38, 42, 41
14, 22, 23, 27, 26, 38, 39, 43, 42
15, 23, 24, 28, 27, 39, 40, 44, 43
17, 26, 27, 31, 30, 42, 43, 47, 46
23, 38, 39, 43, 42, 54, 55, 59, 58
**
********************************** P R O P E R T I E S ************************
*SOLID SECTION, ELSET=EB0, MATERIAL=Default-Steel
*SOLID SECTION, ELSET=EB1, MATERIAL=Default-Steel
**```
Because of large size, the mesh structures for `sphere_3` and
`sphere_5` are not shown here.
## Source
### `spheres.py`
```python
r"""This module, spheres.py, creates a voxelized sphere and exports
it as a .npy file.
Example
-------
source ~/autotwin/automesh/.venv/bin/activate
cd book/examples/spheres
python spheres.py
"""
from pathlib import Path
from typing import Final
from matplotlib.colors import LightSource
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
def sphere(radius: int, dtype=np.uint8) -> np.ndarray:
"""Generate a 3D voxelized representation of a sphere.
Parameters
----------
radius: int
The radius of the sphere. Minimum value is 1.
dtype: data-type, optional
The data type of the output array. Default is np.uint8.
Returns
-------
np.ndarray
A 3D numpy array of shape (2*radius+1, 2*radius+1, 2*radius+1)
representing the voxelized sphere. Voxels within the sphere are
set to 1, and those outside are set to 0.
Raises
------
ValueError
If the radius is less than 1.
Example
-------
>>> sphere(radius=1) returns
array(
[
[[0, 0, 0], [0, 1, 0], [0, 0, 0]],
[[0, 1, 0], [1, 1, 1], [0, 1, 0]],
[[0, 0, 0], [0, 1, 0], [0, 0, 0]]
],
dtype=uint8
)
Reference
---------
Adapted from:
https://github.com/scikit-image/scikit-image/blob/v0.24.0/skimage/morphology/footprints.py#L763-L833
"""
if radius < 1:
raise ValueError("Radius must be >= 1")
n_voxels_per_side = 2 * radius + 1
vox_z, vox_y, vox_x = np.mgrid[
-radius : radius : n_voxels_per_side * 1j,
-radius : radius : n_voxels_per_side * 1j,
-radius : radius : n_voxels_per_side * 1j,
]
voxel_radius_squared = vox_x**2 + vox_y**2 + vox_z**2
result = np.array(voxel_radius_squared <= radius * radius, dtype=dtype)
return result
# User input begin
spheres = {
"radius_1": sphere(radius=1),
"radius_3": sphere(radius=3),
"radius_5": sphere(radius=5),
}
aa = Path(__file__)
bb = aa.with_suffix(".png")
# Visualize the elements.
width, height = 10, 5
# width, height = 8, 4
# width, height = 6, 3
fig = plt.figure(figsize=(width, height))
el, az, roll = 63, -110, 0
cmap = plt.get_cmap(name="tab10")
# NUM_COLORS = len(spheres)
NUM_COLORS = 10 # consistent with tab10 color scheme
VOXEL_ALPHA: Final[float] = 0.9
colors = cmap(np.linspace(0, 1, NUM_COLORS))
lightsource = LightSource(azdeg=325, altdeg=45) # azimuth, elevation
# lightsource = LightSource(azdeg=325, altdeg=90) # azimuth, elevation
DPI: Final[int] = 300 # resolution, dots per inch
SHOW: Final[bool] = False # turn to True to show the figure on screen
SAVE: Final[bool] = False # turn to True to save .png and .npy files
# User input end
N_SUBPLOTS = len(spheres)
IDX = 1
for index, (key, value) in enumerate(spheres.items()):
ax = fig.add_subplot(1, N_SUBPLOTS, index + 1, projection=Axes3D.name)
ax.voxels(
value,
facecolors=colors[index],
edgecolor=colors[index],
alpha=VOXEL_ALPHA,
lightsource=lightsource,
)
ax.set_title(key.replace("_", "="))
IDX += 1
# Set labels for the axes
ax.set_xlabel("x (voxels)")
ax.set_ylabel("y (voxels)")
ax.set_zlabel("z (voxels)")
# Set the camera view
ax.set_aspect("equal")
ax.view_init(elev=el, azim=az, roll=roll)
if SAVE:
cc = aa.with_stem("spheres_" + key)
dd = cc.with_suffix(".npy")
# Save the data in .npy format
np.save(dd, value)
print(f"Saved: {dd}")
fig.tight_layout()
if SHOW:
plt.show()
if SAVE:
fig.savefig(bb, dpi=DPI)
print(f"Saved: {bb}")
test_spheres.py
r"""This module, test_spheres.py, performs point testing of the sphere module.
Example
-------
source ~/autotwin/automesh/.venv/bin/activate
python -m pytest book/examples/spheres/test_spheres.py
"""
import numpy as np
import pytest
import spheres as sph
def test_sphere():
"""Unit tests for the sphere function."""
# Assure that radius >=1 assert is raised
with pytest.raises(ValueError, match="Radius must be >= 1"):
sph.sphere(radius=0)
# Assure radius=1 is correct
gold_r1 = np.array(
[
[[0, 0, 0], [0, 1, 0], [0, 0, 0]],
[[0, 1, 0], [1, 1, 1], [0, 1, 0]],
[[0, 0, 0], [0, 1, 0], [0, 0, 0]],
],
dtype=np.uint8,
)
result_r1 = sph.sphere(radius=1)
assert np.all(gold_r1 == result_r1)
# Assure radius=2 is correct
gold_r2 = np.array(
[
[
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 1, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
],
[
[0, 0, 0, 0, 0],
[0, 1, 1, 1, 0],
[0, 1, 1, 1, 0],
[0, 1, 1, 1, 0],
[0, 0, 0, 0, 0],
],
[
[0, 0, 1, 0, 0],
[0, 1, 1, 1, 0],
[1, 1, 1, 1, 1],
[0, 1, 1, 1, 0],
[0, 0, 1, 0, 0],
],
[
[0, 0, 0, 0, 0],
[0, 1, 1, 1, 0],
[0, 1, 1, 1, 0],
[0, 1, 1, 1, 0],
[0, 0, 0, 0, 0],
],
[
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 1, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
],
],
dtype=np.uint8,
)
result_r2 = sph.sphere(radius=2)
assert np.all(gold_r2 == result_r2)
# Assure radius=3 is correct
gold_r3 = np.array(
[
[
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 1, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
],
[
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 1, 1, 1, 0, 0],
[0, 1, 1, 1, 1, 1, 0],
[0, 1, 1, 1, 1, 1, 0],
[0, 1, 1, 1, 1, 1, 0],
[0, 0, 1, 1, 1, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
],
[
[0, 0, 0, 0, 0, 0, 0],
[0, 1, 1, 1, 1, 1, 0],
[0, 1, 1, 1, 1, 1, 0],
[0, 1, 1, 1, 1, 1, 0],
[0, 1, 1, 1, 1, 1, 0],
[0, 1, 1, 1, 1, 1, 0],
[0, 0, 0, 0, 0, 0, 0],
],
[
[0, 0, 0, 1, 0, 0, 0],
[0, 1, 1, 1, 1, 1, 0],
[0, 1, 1, 1, 1, 1, 0],
[1, 1, 1, 1, 1, 1, 1],
[0, 1, 1, 1, 1, 1, 0],
[0, 1, 1, 1, 1, 1, 0],
[0, 0, 0, 1, 0, 0, 0],
],
[
[0, 0, 0, 0, 0, 0, 0],
[0, 1, 1, 1, 1, 1, 0],
[0, 1, 1, 1, 1, 1, 0],
[0, 1, 1, 1, 1, 1, 0],
[0, 1, 1, 1, 1, 1, 0],
[0, 1, 1, 1, 1, 1, 0],
[0, 0, 0, 0, 0, 0, 0],
],
[
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 1, 1, 1, 0, 0],
[0, 1, 1, 1, 1, 1, 0],
[0, 1, 1, 1, 1, 1, 0],
[0, 1, 1, 1, 1, 1, 0],
[0, 0, 1, 1, 1, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
],
[
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 1, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
],
],
dtype=np.uint8,
)
result_r3 = sph.sphere(radius=3)
assert np.all(gold_r3 == result_r3)
Defeaturing
Defeaturing is accomplished by specifying a voxel threshold. A cluster of voxels, defined as two or more voxels that share a face (edge and node sharing do not constitute a cluster) with count at or above the threshold will be preserved, whereas a cluster of voxels with a count below the threshold will be eliminated through resorption into the surrounding material.
Example
With Python, we created a segmentation of four circular blobs with noise placed randomly in a bounding box, shown in left of the figure below. The segmentation file blobs.npy was then used as the input to automesh with the defeature command. The output file blobs_defeatured.npy is shown in the right of the figure. The threshold was set to 20 voxels.
automesh defeature -i blobs.npy -o blobs_defeatured.npy -m 20
Both the segmentation files, original and defeatured, were then converted to a mesh and visualized in Hexalab.
Figure: (left) Four circular blobs with noise (blobs.npy) used as input to the defeature command, (right) the output defeatured segmentation (blobs_defeatured.npy).
Source
defeature.py
r"""This module creates spheres and blobs inside of a domain for the purposes
of illustrating the defeature command.
Example:
source ~/autotwin/automesh/.venv/bin/activate
cd ~/autotwin/automesh/book/analysis/defeature
python defeature.py
"""
import logging
from pathlib import Path
import random
import subprocess
from typing import Final
import numpy as np
DOMAIN_SIZE: Final[int] = 128
NUM_SPHERES: Final[int] = 4
RADIUS_MAX: Final[int] = 20
FN_SPHERE_STEM = "spheres"
FN_BLOB_STEM = "blobs"
# Configure logging
logging.basicConfig(
level=logging.INFO,
format="%(levelname)s: %(message)s",
)
def create_spheres(data: np.ndarray, num_spheres: int, radius_max: int) -> None:
"""Creates random spheres in a 3D binary array.
Parameters:
data: A 3D binary array representing the domain.
num_spheres: The number of spheres to create.
radius_max: The radius of the spheres.
"""
shape = data.shape
(xmin, ymin, zmin) = (0, 0, 0)
(xmax, ymax, zmax) = (shape[0] - 1, shape[1] - 1, shape[2] - 1)
for _ in range(num_spheres):
# Randomly choose a center for the sphere
center = np.array(
[
random.randint(xmin, xmax),
random.randint(ymin, ymax),
random.randint(zmin, zmax),
]
)
# Randomly choose a center for the sphere
radius = random.randint(1, radius_max)
# Create a grid of indices
z, y, x = np.indices(shape)
# Calculate the distance from the center
distance = np.sqrt(
(x - center[0]) ** 2 + (y - center[1]) ** 2 + (z - center[2]) ** 2
)
# Set the voxels within the radius to 1
data[distance <= radius] = 1
def create_blob(data: np.ndarray, center: np.ndarray, radius_max: int) -> None:
"""Creates a sphere-like blob in a 3D binary array.
Parameters:
data: A 3D binary array representing the domain.
center: The center of the blob.
radius_max: The maximum radius of the blob.
"""
# Create a grid of indices
z, y, x = np.indices(data.shape)
# Calculate the distance from the center
distance = np.sqrt(
(x - center[0]) ** 2 + (y - center[1]) ** 2 + (z - center[2]) ** 2
)
# Create a random radius for each voxel based on a Gaussian distribution
radius_variation = np.random.normal(
loc=radius_max, scale=radius_max * 0.5, size=data.shape
)
# Set the voxels to 1 if they are within the radius variation
data[distance <= radius_variation] = 1
def create_blobs(data: np.ndarray, num_blobs: int, radius_max: int) -> None:
"""Create a number of sphere-like blobs in a 3D binary array.
Parameters:
data: A 3D binary array representing the domain.
num_blobs: The number of blobs to create.
radius_max: The maximum radius of the blobs.
"""
shape = data.shape
(xmin, ymin, zmin) = (0, 0, 0)
(xmax, ymax, zmax) = (shape[0] - 1, shape[1] - 1, shape[2] - 1)
for _ in range(num_blobs):
# Randomly choose a center for the blob
center = np.array(
[
random.randint(xmin, xmax),
random.randint(ymin, ymax),
random.randint(zmin, zmax),
]
)
# Create a blob at the center
create_blob(data=data, center=center, radius_max=radius_max)
def run_commands(commands: list) -> None:
"""Run a list of commands in the shell.
Parameters:
commands: A list of command strings to run.
"""
for command in commands:
try:
logging.info("Running command: %s", " ".join(command))
result = subprocess.run(command, check=True, capture_output=True, text=True)
logging.info("Command output: %s", result.stdout)
except subprocess.CalledProcessError as e:
logging.error("Error running command:")
logging.error("Command: %s", " ".join(command))
logging.error("Return code: %s", e.returncode)
logging.error("Standard Output: %s", e.stdout)
logging.error("Standard Error: %s", e.stderr)
def spheres():
"""Create and save a 3D binary array with random spheres."""
# Initialize the domain filled with zeros
domain = np.zeros((DOMAIN_SIZE, DOMAIN_SIZE, DOMAIN_SIZE), dtype=np.uint8)
# Create spheres in the domain
create_spheres(data=domain, num_spheres=NUM_SPHERES, radius_max=RADIUS_MAX)
# Save the data to a .npy file
FN_SPHERE = f"{FN_SPHERE_STEM}.npy"
np.save(FN_SPHERE, domain)
print(f"The domain with spheres has been saved to:\n{FN_SPHERE}.")
# Create the mesh with automesh
automesh = Path("~/autotwin/automesh/target/release/automesh").expanduser()
assert automesh.is_file(), f"automesh not found at {automesh}"
FN_SPHERE_EXO = f"{FN_SPHERE_STEM}.exo"
FN_SPHERE_MESH = f"{FN_SPHERE_STEM}.mesh"
commands = [
[
str(automesh),
"mesh",
"hex",
"-i",
str(FN_SPHERE),
"-o",
str(FN_SPHERE_EXO),
"-r",
"0",
],
[
str(automesh),
"mesh",
"hex",
"-i",
str(FN_SPHERE),
"-o",
str(FN_SPHERE_MESH),
"-r",
"0",
],
]
run_commands(commands=commands)
def blobs():
"""Create and save a 3D binary array with random blobs."""
# Initialize the domain filled with zeros
domain = np.zeros((DOMAIN_SIZE, DOMAIN_SIZE, DOMAIN_SIZE), dtype=np.uint8)
# Create blobs in the domain
create_blobs(data=domain, num_blobs=NUM_SPHERES, radius_max=RADIUS_MAX)
# Save the data to a .npy file
FN_BLOB = f"{FN_BLOB_STEM}.npy"
FN_BLOB_DEFEATURED = f"{FN_BLOB_STEM}_defeatured.npy"
np.save(FN_BLOB, domain)
print(f"The domain with blobs has been saved to:\n{FN_BLOB}.")
# Create the mesh with automesh
automesh = Path("~/autotwin/automesh/target/release/automesh").expanduser()
assert automesh.is_file(), f"automesh not found at {automesh}"
FN_BLOB_EXO = f"{FN_BLOB_STEM}.exo"
FN_BLOB_MESH = f"{FN_BLOB_STEM}.mesh"
FN_BLOB_DEFEATURED_EXO = f"{FN_BLOB_STEM}_defeatured.exo"
FN_BLOB_DEFEATURED_MESH = f"{FN_BLOB_STEM}_defeatured.mesh"
commands = [
[
str(automesh),
"mesh",
"hex",
"-i",
str(FN_BLOB),
"-o",
str(FN_BLOB_EXO),
"-r",
"0",
],
[
str(automesh),
"mesh",
"hex",
"-i",
str(FN_BLOB),
"-o",
str(FN_BLOB_MESH),
"-r",
"0",
],
[
str(automesh),
"defeature",
"-i",
str(FN_BLOB),
"-o",
str(FN_BLOB_DEFEATURED),
"-m",
"20",
],
[
str(automesh),
"mesh",
"hex",
"-i",
str(FN_BLOB_DEFEATURED),
"-o",
str(FN_BLOB_DEFEATURED_EXO),
"-r",
"0",
],
[
str(automesh),
"mesh",
"hex",
"-i",
str(FN_BLOB_DEFEATURED),
"-o",
str(FN_BLOB_DEFEATURED_MESH),
"-r",
"0",
],
]
run_commands(commands=commands)
if __name__ == "__main__":
spheres()
blobs()
Smoothing
Introduction
Both Laplacian smoothing1 and Taubin smoothing2 3 are smoothing operations that adjust the positions of the nodes in a finite element mesh.
Laplacian smoothing, based on the Laplacian operator, computes the average position of a point's neighbors and moves the point toward the average. This reduces high-frequency noise but can result in a loss of shape and detail, with overall shrinkage.
Taubin smoothing is an extension of Laplacian smoothing that seeks to overcome the shrinkage drawback associated with the Laplacian approach. Taubin is a two-pass approach. The first pass smooths the mesh. The second pass re-expands the mesh.
Laplacian Smoothing
Consider a subject node with position . The subject node connects to neighbor points for through edges.
For concereteness, consider a node with four neighbors, shown in the figure below.
Figure: The subject node with edge connections (dotted lines) to neighbor nodes with (withouth loss of generality, the specific example of is shown). The average position of all neighbors of is denoted , and the gap (dashed line) originates at and terminates at .
Define as the average position of all neighbors of ,
Define the gap vector as originating at and terminating at (viz., ),
Let be the positive scaling factor for the gap .
Since
subdivision of this relationship into several substeps gives rise to an iterative approach. We typically select to avoid overshoot of the update, .
At iteration , we update the position of by an amount to as
with
Thus
and finally
The formulation above, based on the average position of the neighbors, is a special case of the more generalized presentation of Laplace smoothing, wherein a normalized weighting factor, , is used:
When all weights are equal and normalized by the number of neighbors, , the special case presented in the box above is recovered.
Example
For a 1D configuration, consider a node with initial position with two neighbors (that never move) with positions and (). With , the table below shows updates for for position .
Table: Iteration updates of a 1D example.
| 0 | 0.5 | 1.5 | -1 | -0.3 |
| 1 | 0.5 | 1.2 | -0.7 | -0.21 |
| 2 | 0.5 | 0.99 | -0.49 | -0.147 |
| 3 | 0.5 | 0.843 | -0.343 | -0.1029 |
| 4 | 0.5 | 0.7401 | -0.2401 | -0.07203 |
| 5 | 0.5 | 0.66807 | -0.16807 | -0.050421 |
| 6 | 0.5 | 0.617649 | -0.117649 | -0.0352947 |
| 7 | 0.5 | 0.5823543 | -0.0823543 | -0.02470629 |
| 8 | 0.5 | 0.55764801 | -0.05764801 | -0.017294403 |
| 9 | 0.5 | 0.540353607 | -0.040353607 | -0.012106082 |
| 10 | 0.5 | 0.528247525 | -0.028247525 | -0.008474257 |
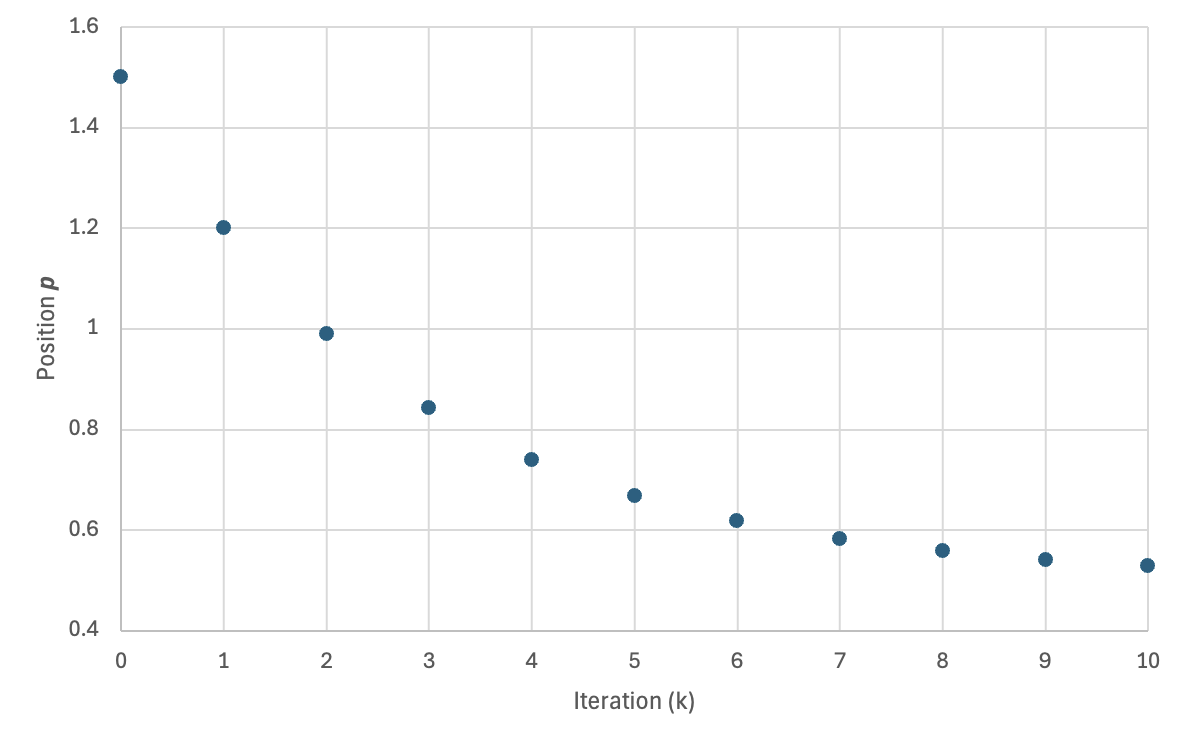
Figure: Convergence of position toward as a function of iteration .
Taubin Smoothing
Taubin smoothing is a two-parameter, two-pass iterative variation of Laplace smoothing. Specifically with the definitions used in Laplacian smoothing, a second negative parameter is used, where
The first parameter, , tends to smooth (and shrink) the domain. The second parameter, , tends to expand the domain.
Taubin smoothing is written, for , , , with typically being even, as
- First pass (if is even):
- Second pass (if is odd):
In any second pass (any pass with odd), the algorithm uses the updated positions from the previous (even) iteration to compute the new positions. So, the average is taken from the updated neighbor positions rather than the original neighbor positions. Some presentation of Taubin smoothing do not carefully state the second pass update, and so we emphasize it here.
Taubin Parameters
We follow the recommendations of Taubin3 for selecting values of and , with specific details noted as follows: We use the second degree polynomial transfer function,
with as the domain of interest since the eigenvalues of the discrete Laplacian being approximated all are within .3
There is a value of called the pass-band frequency, ,
such that for all values of and .
Given that , the pass-band and
Taubin noted that values of "...from 0.01 to 0.1 produce good results, and all examples shown in this paper were computed with ." Taubin also noted that for , choice of such that "...ensures a stable and fast filter."
We implement the following default values:
- ,
which provides and .
Hierarchical Control
As a default, all nodes in the mesh are free nodes, meaning they are subject to updates in position due to smoothing.
- Free nodes
For the purpose of hierarchical smoothing, we categorize all nodes as belonging to one of the following categories.
- Boundary nodes
- Nodes on the exterior of the domain and nodes that lie at the interface of two different blocks are reclassified from free nodes to boundary nodes.
- Like free nodes, these nodes are also subject to updates in position due to smoothing.
- Unlike free nodes, which are influenced by positions of neighboring nodes of any category, boundary nodes are only influenced positions of other boundary nodes, or prescribed nodes (described below).
- Interior nodes
- The free nodes not categorized as boundary nodes are categorized as interior nodes.
- Interior nodes are influenced by neighboring nodes of all categories.
- Prescribed nodes
- Finally, we may wish to select nodes, typically but not necessarily from boundary nodes, to move to a specific location, often to match the desired shape of a mesh. These nodes are reclassified as prescribed nodes.
- Prescribed nodes are not subject to updates in position due to smoothing because they are a priori prescribed to reside at a given location.
This classification is shown below in figures. All nodes in the mesh are categorized as FREE nodes:

Nodes that lie on the exterior and/or an interface are categoried as BOUNDARY nodes. The remaining free nodes that are not BOUNDARY nodes are INTERIOR nodes.
Some INTERIOR and BOUNDARY nodes may be recategorized as PRESCRIBED nodes.
Note that this focuses on regular volumetric finite element meshes, and does not apply to certain other meshes. For example, manifold surface meshes embedded in three dimensions have only interior nodes, so hierarchical control would not apply.
The Hierarchy enum
These three categories, INTERIOR, BOUNDARY, and PRESCRIBED, compose the hierarchical structure of hierarchical smoothing. Nodes are classified in code with the following enum,
class Hierarchy(Enum):
"""All nodes must be categorized as beloning to one, and only one,
of the following hierarchical categories.
"""
INTERIOR = 0
BOUNDARY = 1
PRESCRIBED = 2
Hierarchical Control
Hierarchical control classifies all nodes in a mesh as belonging to a interior , boundary , or prescribed . These categories are mutually exclusive. Any and all nodes must belong to one, and only one, of these three categories. For a given node , let
- the set of interior neighbors be denoted ,
- the set of boundary neighbors be denoted , and
- the set of prescribed neighbors be denoted .
Hierarchical control redefines a node's neighborhood according to the following hierarchical rules:
- for any interior node , nodes , , and are neighbors; there is no change in the neighborhood,
- for any boundary node , only boundary nodes and prescribed nodes are neighbors; a boundary node neighborhood exludes interior nodes, and
- for any prescribed node , all neighbors of any category are excluded; the prescribed node's position does not change during smoothing.
The following figure shows this concept:
Figure: Classification of nodes into categories of interior nodes , boundary nodes , and prescribed nodes . Hierarchical relationship: An interior node's smooothing neighbors are nodes of any category, a boundary node's smoothing neighbors are other boundary nodes or other prescribed nodes, and prescribed nodes have no smoothing neighbors.
Relationship to a SideSet
A SideSet is a set of nodes on the boundary of a domain, used to prescribe a boundary condition on the finite element mesh.
- A subset of nodes on the boundary nodes is classified as exterior nodes.
- A different subset of nodes on the boundary is classified as interface nodes.
- A
SideSetis composed of either exterior nodes or interface nodes. - Because a node can lie both on the exterior and on an interface, some nodes (shown in red) are included in both the exterior nodes and the interface nodes.

Chen Example
Chen4 used medical image voxel data to create a structured hexahedral mesh. They noded that the approach generated a mesh with "jagged edges on mesh surface and material interfaces," which can cause numerical artifacts.
Chen used hierarchical Taubin mesh smoothing for eight (8) iterations, with and to smooth the outer and inner surfaces of the mesh.
References
-
Sorkine O. Laplacian mesh processing. Eurographics (State of the Art Reports). 2005 Sep;4(4):1. paper ↩
-
Taubin G. Curve and surface smoothing without shrinkage. In Proceedings of IEEE international conference on computer vision 1995 Jun 20 (pp. 852-857). IEEE. paper ↩
-
Taubin G. A signal processing approach to fair surface design. In Proceedings of the 22nd annual conference on Computer graphics and interactive techniques 1995 Sep 15 (pp. 351-358). paper ↩ ↩2 ↩3
-
Chen Y, Ostoja-Starzewski M. MRI-based finite element modeling of head trauma: spherically focusing shear waves. Acta mechanica. 2010 Aug;213(1):155-67. paper ↩
Laplace Smoothing
Double X
We examine the most basic type of smoothing, Laplace smoothing, , without hierarchical control, with the Double X example.

Figure: The Double X two-element example.
Table. The neighborhoods table. A node, with its neighbors, is considered a single neighborhood. The table has twelve neighborhoods.
| node | node neighbors |
|---|---|
| 1 | 2, 4, 7 |
| 2 | 1, 3, 5, 8 |
| 3 | 2, 6, 9 |
| 4 | 1, 5, 10 |
| 5 | 2, 4, 6, 11 |
| 6 | 3, 5, 12 |
| 7 | 1, 8, 10 |
| 8 | 2, 7, 9, 11 |
| 9 | 3, 8, 12 |
| 10 | 4, 7, 11 |
| 11 | 5, 8, 10, 12 |
| 12 | 6, 9, 11 |
Hierarchy
Following is a test where all nodes are BOUNDARY from the Hierarchy enum.
node_hierarchy: NodeHierarchy = (
Hierarchy.BOUNDARY,
Hierarchy.BOUNDARY,
Hierarchy.BOUNDARY,
Hierarchy.BOUNDARY,
Hierarchy.BOUNDARY,
Hierarchy.BOUNDARY,
Hierarchy.BOUNDARY,
Hierarchy.BOUNDARY,
Hierarchy.BOUNDARY,
Hierarchy.BOUNDARY,
Hierarchy.BOUNDARY,
Hierarchy.BOUNDARY,
)
Since there are no
INTERIORnodes norPRESCRIBEDnodes, the effect of hiearchical smoothing is nill, and the same effect would be observed were all nodes categorized asINTERIORnodes.
Iteration 1
Table: The smoothed configuration (x, y, z) after one iteration of Laplace smoothing.
| node | x | y | z |
|---|---|---|---|
| 1 | 0.1 | 0.1 | 0.1 |
| 2 | 1.0 | 0.075 | 0.075 |
| 3 | 1.9 | 0.1 | 0.1 |
| 4 | 0.1 | 0.9 | 0.1 |
| 5 | 1.0 | 0.925 | 0.075 |
| 6 | 1.9 | 0.9 | 0.1 |
| 7 | 0.1 | 0.1 | 0.9 |
| 8 | 1.0 | 0.075 | 0.925 |
| 9 | 1.9 | 0.1 | 0.9 |
| 10 | 0.1 | 0.9 | 0.9 |
| 11 | 1.0 | 0.925 | 0.925 |
| 12 | 1.9 | 0.9 | 0.9 |
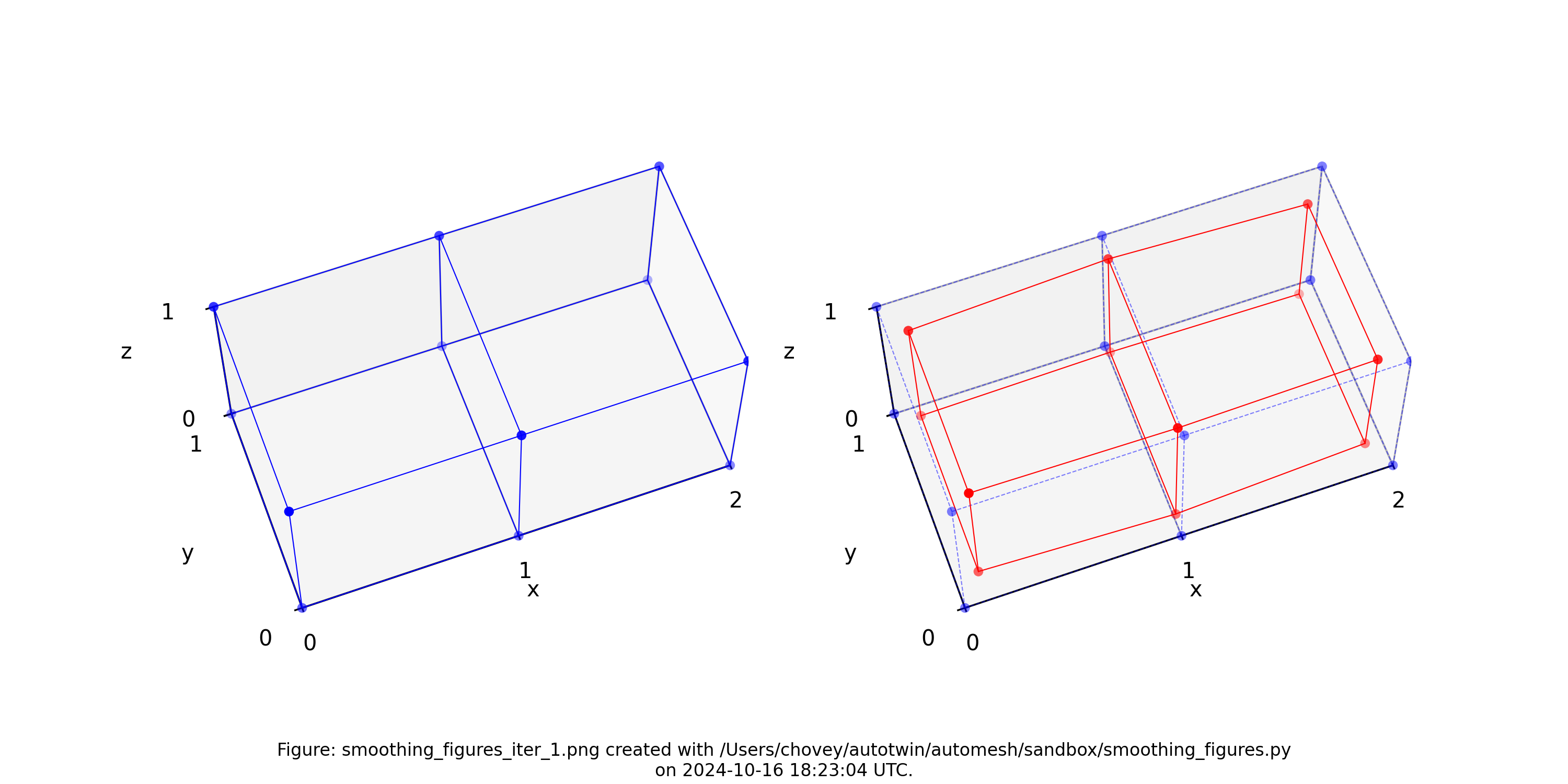
Figure: Two element test problem (left) original configuration, (right) subject to one iteration of Laplace smoothing.
Iteration 2
| node | x | y | z |
|---|---|---|---|
| 1 | 0.19 | 0.1775 | 0.1775 |
| 2 | 1.0 | 0.1425 | 0.1425 |
| 3 | 1.81 | 0.1775 | 0.1775 |
| 4 | 0.19 | 0.8225 | 0.1775 |
| 5 | 1.0 | 0.8575 | 0.1425 |
| 6 | 1.81 | 0.8225 | 0.1775 |
| 7 | 0.19 | 0.1775 | 0.8225 |
| 8 | 1.0 | 0.1425 | 0.8575 |
| 9 | 1.81 | 0.1775 | 0.8225 |
| 10 | 0.19 | 0.8225 | 0.8225 |
| 11 | 1.0 | 0.8575 | 0.8575 |
| 12 | 1.81 | 0.8225 | 0.8225 |

Figure: Two element test problem (left) original configuration, (right) subject to two iterations of Laplace smoothing.
Iteration 100
A known drawback of Laplace smoothing is that it can fail to preserve volumes. In the limit, volumes get reduced to a point, as illustrated in the figure below.
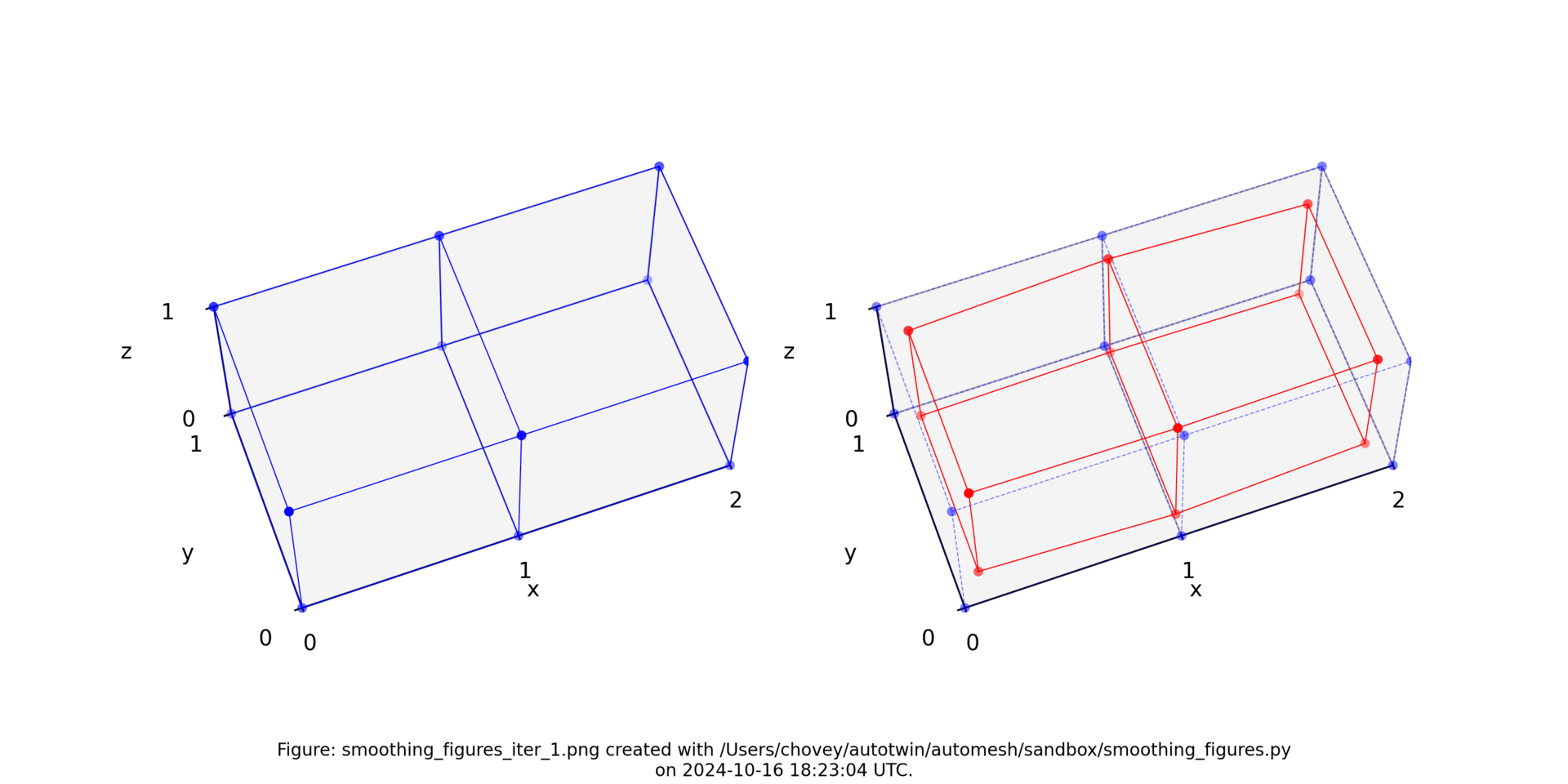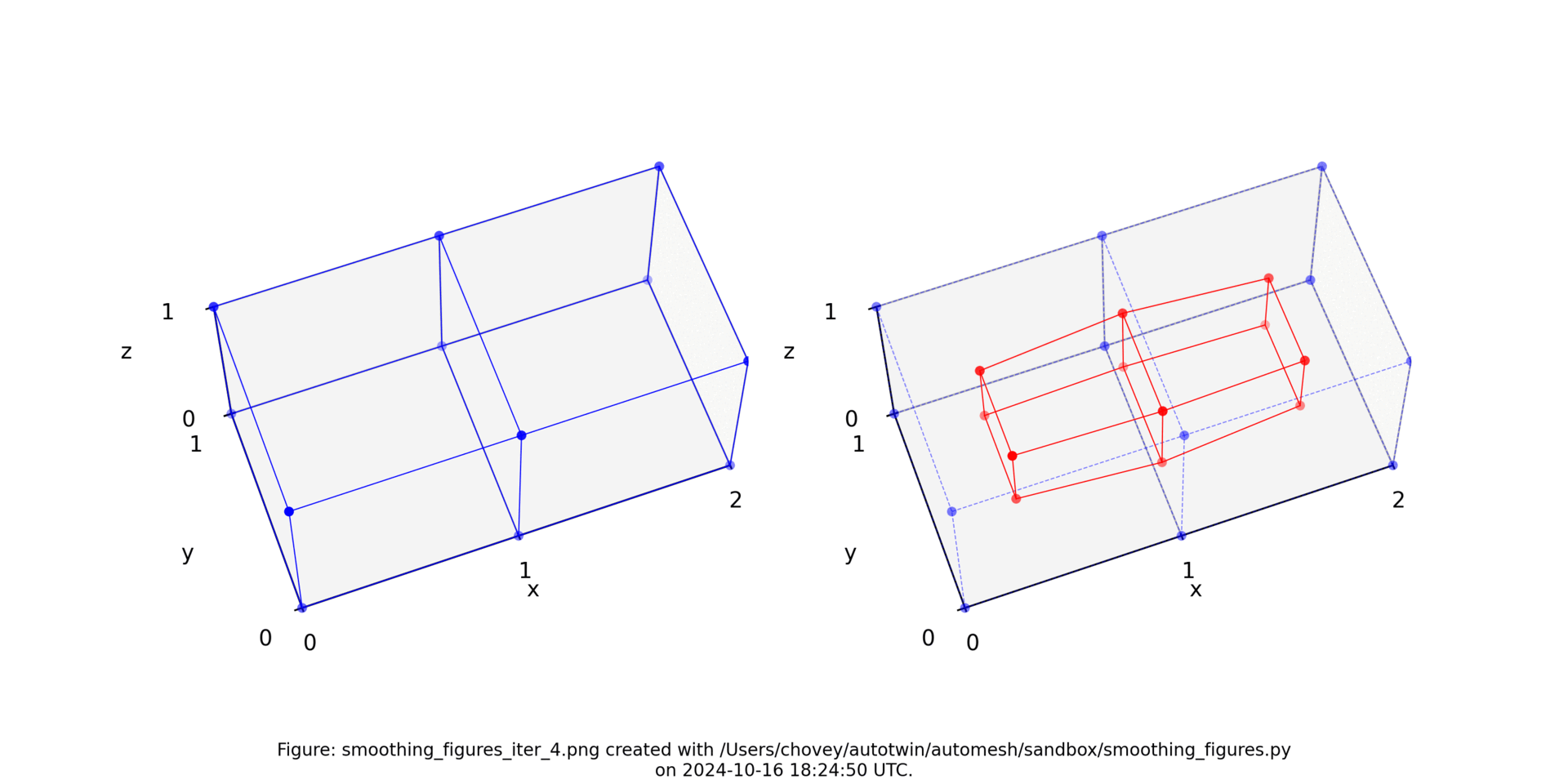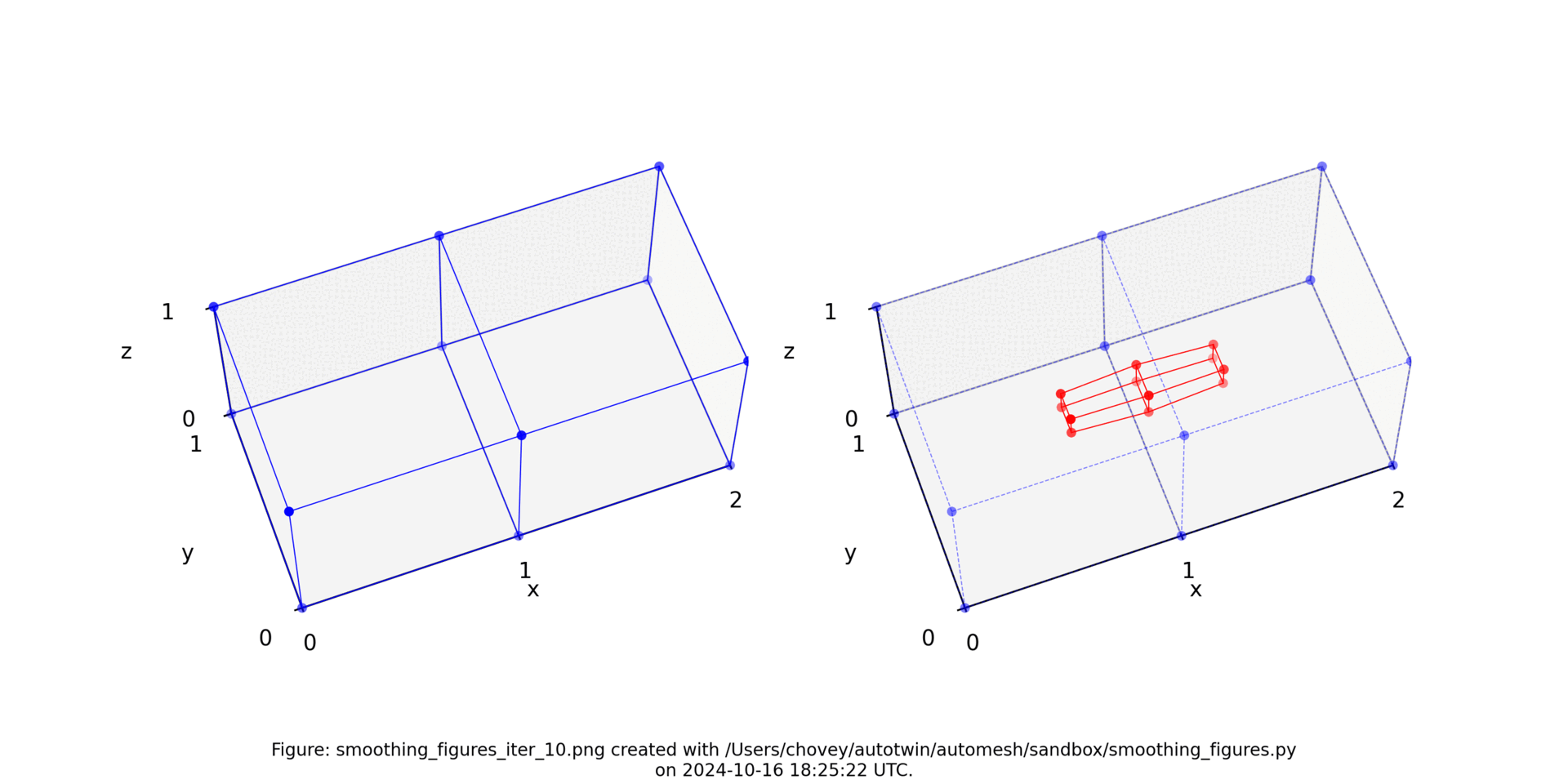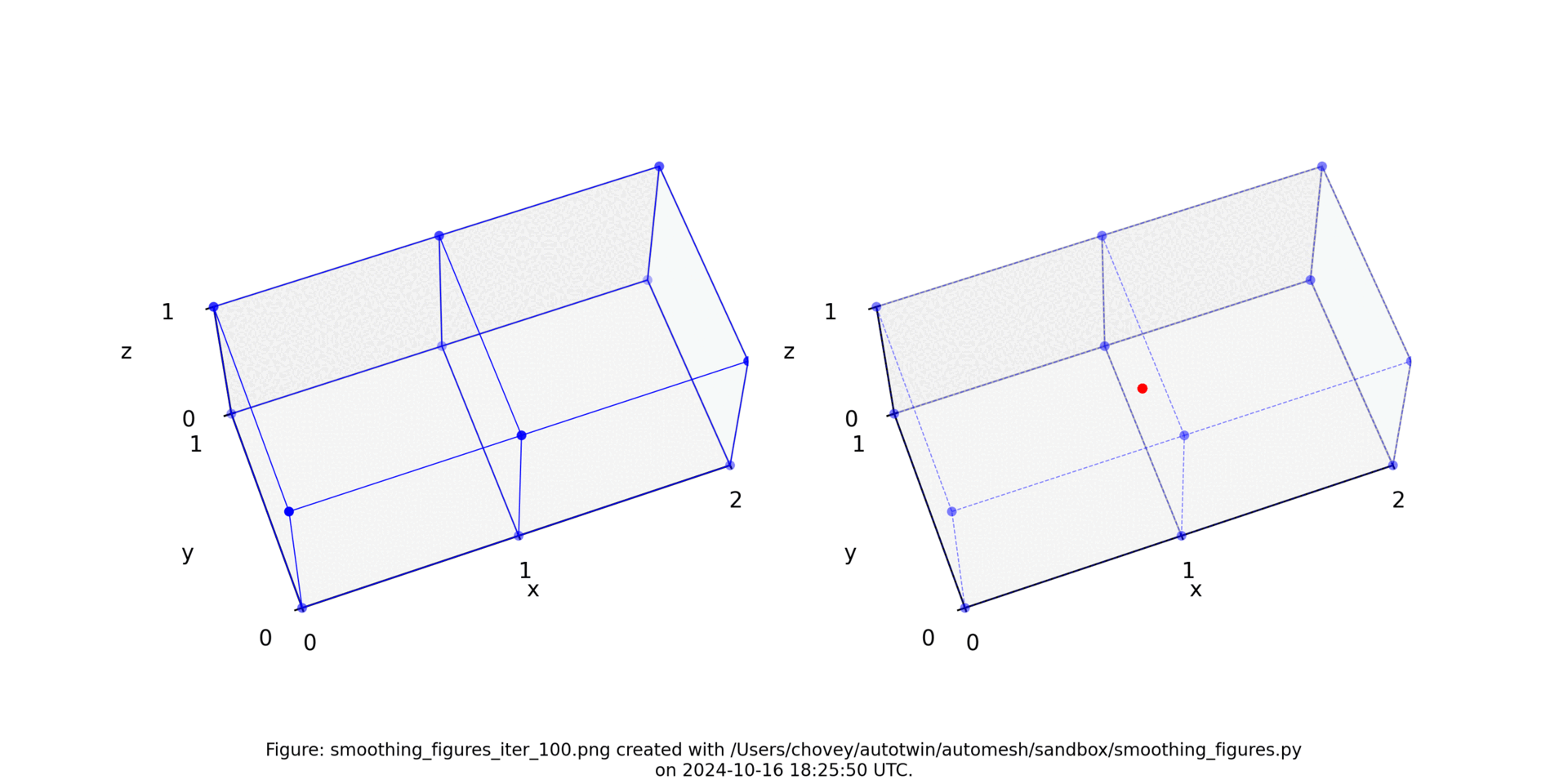
Figure: Two element test problem (left) original configuration, (right) subject to [1, 2, 3, 4, 5, 10, 20, 30, 100 iterations of Laplace smoothing. Animation created with Ezgif.
Laplace Smoothing with Hierarchical Control
Laplace Smoothing, Hierarchical Control, Prescribed Homogeneous
Cube with Inclusion

To come.
Laplace Smoothing, Hierarchical Control, Prescribed Inhomogeneous
Bracket
To begin to examine hiearchical control, we consider the Bracket example.

Figure: The Bracket example.
Laplace Smoothing without Hierarchical Control
As a baseline, let's examine what Laplace smoothing, , without hierarchical control performs.
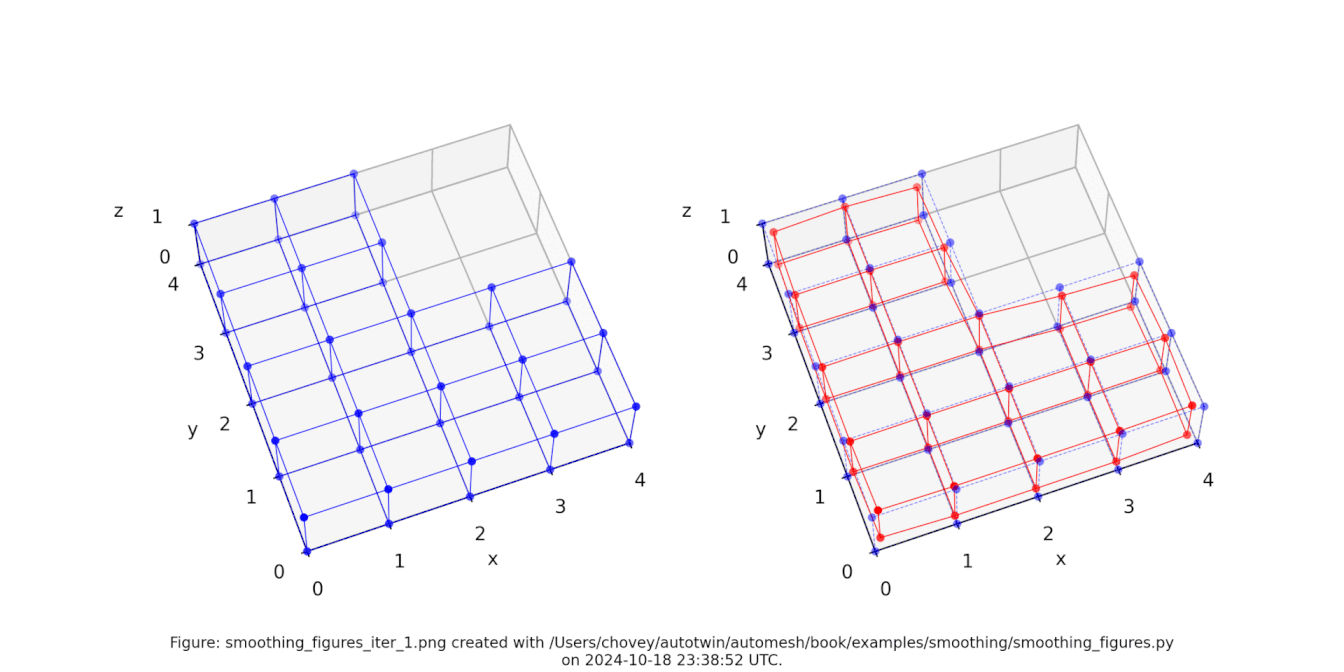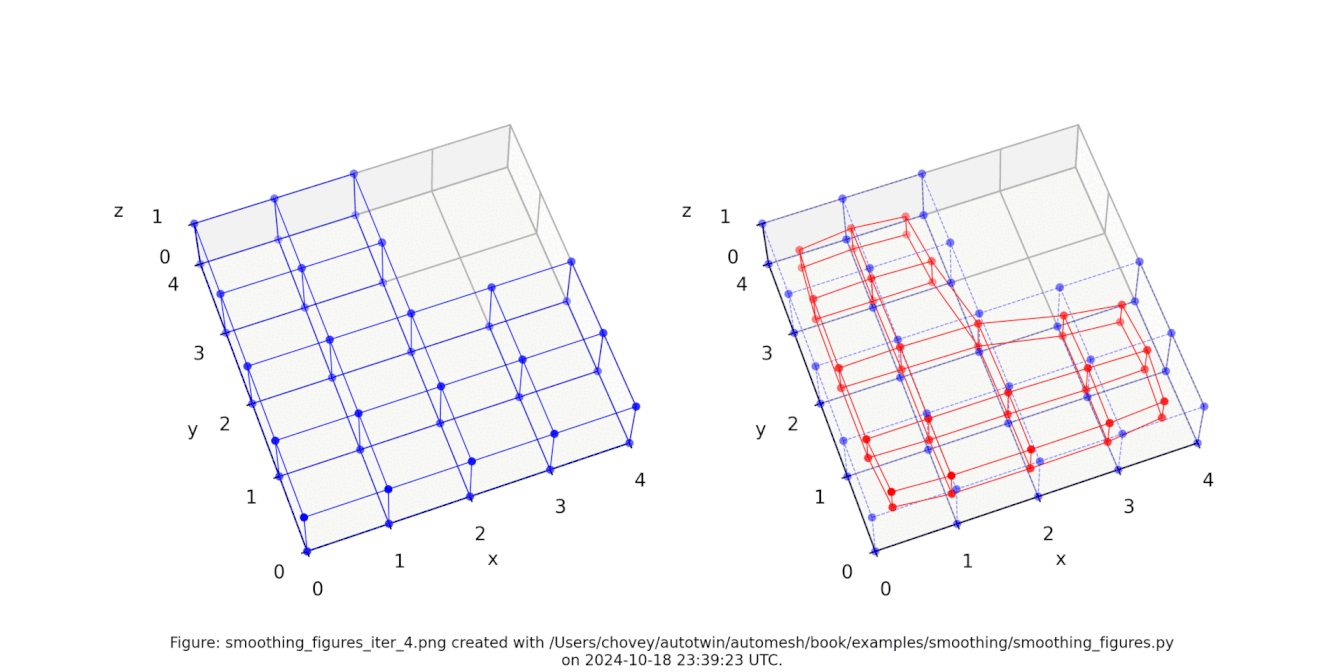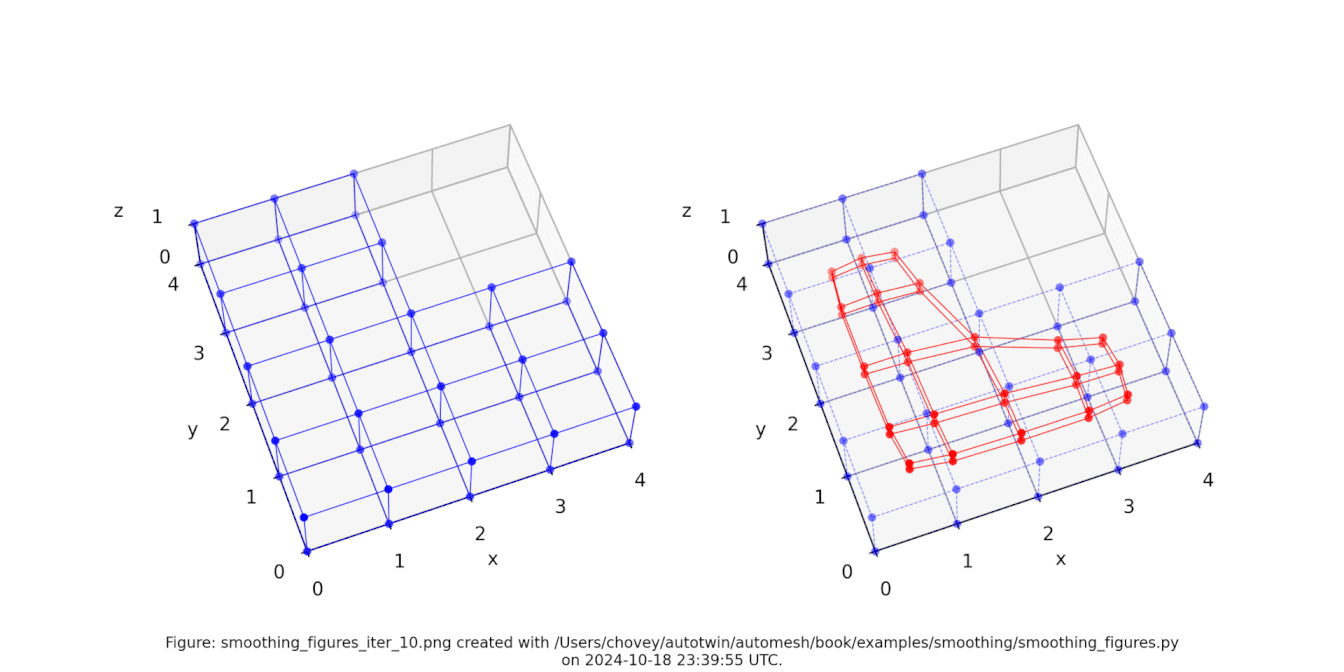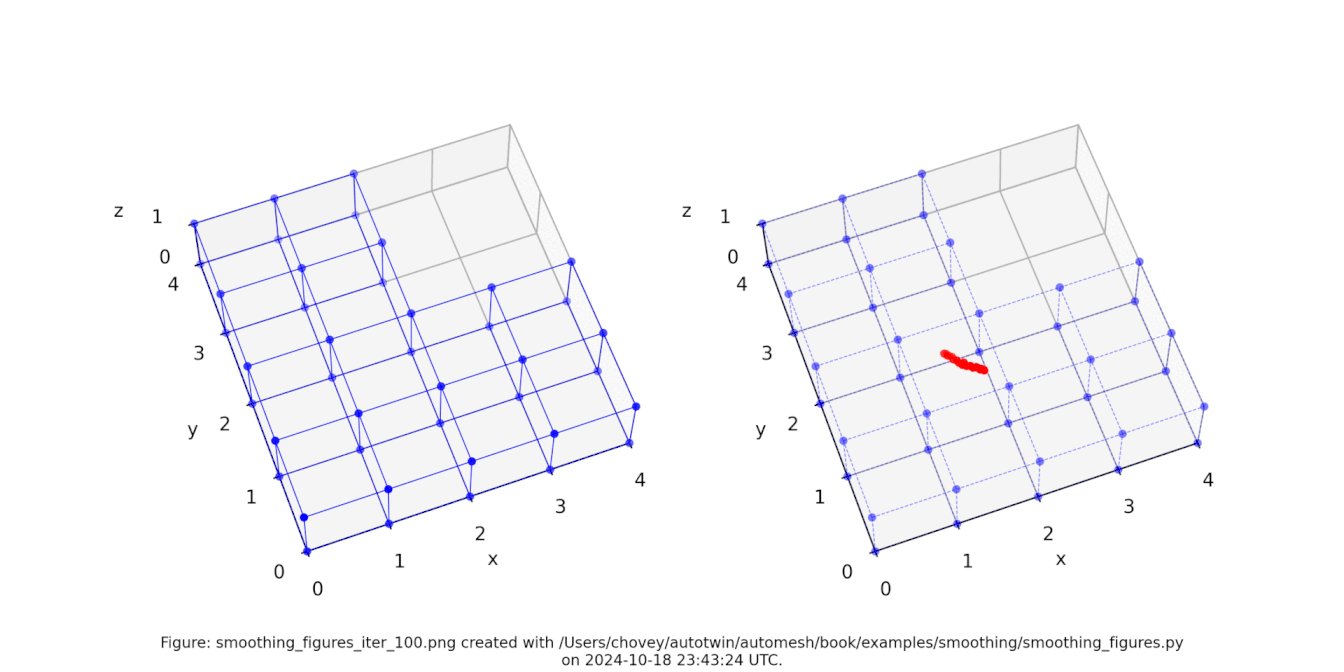
Figure: The Bracket test problem (left) original configuration, (right) subject to [1, 2, 3, 4, 5, 10, 20, 30, 100] iterations of Laplace smoothing. Animation created with Ezgif.
As an example, the nodal positions after 10 iterations are as follows:
| node | x | y | z |
|---|---|---|---|
| 1 | 0.6603416706977089 | 0.6603416706977089 | 0.42058348557613 |
| 2 | 1.164014406316456 | 0.5922705223353653 | 0.4003570849733875 |
| 3 | 1.9979372129260855 | 0.5706936094999626 | 0.39548539946279243 |
| 4 | 2.8325693635137097 | 0.5703120664922405 | 0.40180333889841546 |
| 5 | 3.332396179530681 | 0.6196854057408008 | 0.4228468310236131 |
| 6 | 0.5922705223353653 | 1.164014406316456 | 0.4003570849733875 |
| 7 | 1.129330412354556 | 1.129330412354556 | 0.3779268501553354 |
| 8 | 1.986117815900869 | 1.100245269915641 | 0.3744217105825115 |
| 9 | 2.8536168286772536 | 1.0284532492877596 | 0.3839611664938703 |
| 10 | 3.3805688588919414 | 1.007196857251266 | 0.40846995582593837 |
| 11 | 0.5706936094999626 | 1.9979372129260853 | 0.39548539946279243 |
| 12 | 1.100245269915641 | 1.986117815900869 | 0.37442171058251145 |
| 13 | 1.9089262792820898 | 1.90892627928209 | 0.3766933485101331 |
| 14 | 2.816962753463538 | 1.5457873563122884 | 0.3970154773256839 |
| 15 | 3.3296020281899956 | 1.409074280806729 | 0.42165070606234384 |
| 16 | 0.5703120664922405 | 2.8325693635137097 | 0.40180333889841546 |
| 17 | 1.0284532492877596 | 2.8536168286772536 | 0.3839611664938703 |
| 18 | 1.5457873563122884 | 2.816962753463538 | 0.3970154773256839 |
| 19 | 0.6196854057408008 | 3.332396179530681 | 0.4228468310236131 |
| 20 | 1.007196857251266 | 3.3805688588919414 | 0.40846995582593837 |
| 21 | 1.409074280806729 | 3.3296020281899956 | 0.42165070606234384 |
| 22 | 0.6603416706977089 | 0.6603416706977089 | 0.5794165144238701 |
| 23 | 1.164014406316456 | 0.5922705223353653 | 0.5996429150266126 |
| 24 | 1.9979372129260853 | 0.5706936094999626 | 0.6045146005372077 |
| 25 | 2.8325693635137097 | 0.5703120664922404 | 0.5981966611015848 |
| 26 | 3.332396179530681 | 0.6196854057408007 | 0.5771531689763871 |
| 27 | 0.5922705223353654 | 1.164014406316456 | 0.5996429150266126 |
| 28 | 1.129330412354556 | 1.129330412354556 | 0.6220731498446648 |
| 29 | 1.986117815900869 | 1.100245269915641 | 0.6255782894174887 |
| 30 | 2.8536168286772536 | 1.0284532492877596 | 0.6160388335061299 |
| 31 | 3.3805688588919414 | 1.0071968572512657 | 0.5915300441740619 |
| 32 | 0.5706936094999626 | 1.9979372129260853 | 0.6045146005372076 |
| 33 | 1.100245269915641 | 1.986117815900869 | 0.6255782894174885 |
| 34 | 1.90892627928209 | 1.9089262792820898 | 0.623306651489867 |
| 35 | 2.816962753463538 | 1.5457873563122881 | 0.6029845226743162 |
| 36 | 3.3296020281899956 | 1.409074280806729 | 0.5783492939376563 |
| 37 | 0.5703120664922404 | 2.8325693635137097 | 0.5981966611015848 |
| 38 | 1.0284532492877596 | 2.8536168286772536 | 0.6160388335061298 |
| 39 | 1.5457873563122884 | 2.816962753463538 | 0.6029845226743162 |
| 40 | 0.6196854057408007 | 3.332396179530681 | 0.5771531689763871 |
| 41 | 1.0071968572512657 | 3.3805688588919414 | 0.5915300441740617 |
| 42 | 1.409074280806729 | 3.3296020281899956 | 0.5783492939376562 |
Laplace Smoothing with Hierarchical Control
We illustrate the how hierarchical control affects the Laplace smoothing.
Conside the PRESCRIBED and BOUNDARY node hierarchy below:
node_hierarchy: NodeHierarchy = (
# hierarchy enum, node number, prescribed (x, y, z)
Hierarchy.PRESCRIBED, # 1 -> (0, 0, 0)
Hierarchy.PRESCRIBED, # 2 -> (1, 0, 0)
Hierarchy.PRESCRIBED, # 3 -> (2, 0, 0)
Hierarchy.PRESCRIBED, # 4 -> (3, 0, 0)
Hierarchy.PRESCRIBED, # 5 -> (4, 0, 0)
Hierarchy.PRESCRIBED, # 6 -> (0, 1, 0)
Hierarchy.BOUNDARY, # 7
Hierarchy.BOUNDARY, # 8
Hierarchy.BOUNDARY, # 9
Hierarchy.PRESCRIBED, # 10 -> (4.5*cos(15 deg), 4.5*sin(15 deg), 0)
Hierarchy.PRESCRIBED, # 11 -> *(0, 2, 0)
Hierarchy.BOUNDARY, # 12
Hierarchy.BOUNDARY, # 13
Hierarchy.BOUNDARY, # 14
Hierarchy.PRESCRIBED, # 15 -> (4.5*cos(30 deg), 4.5*sin(30 deg), 0)
Hierarchy.PRESCRIBED, # 16 -> (0, 3, 0)
Hierarchy.BOUNDARY, # 17
Hierarchy.BOUNDARY, # 18
Hierarchy.PRESCRIBED, # 19 -> (0, 4, 0)
Hierarchy.PRESCRIBED, # 20 -> (1.5, 4, 0)
Hierarchy.PRESCRIBED, # 21 -> (3.5, 4, 0)
#
Hierarchy.PRESCRIBED, # 22 -> (0, 0, 1)
Hierarchy.PRESCRIBED, # 23 -> (1, 0, 1)
Hierarchy.PRESCRIBED, # 24 -> (2, 0, 1)
Hierarchy.PRESCRIBED, # 25 -> (3, 0, 1)
Hierarchy.PRESCRIBED, # 26 -> (4, 0, 1)
Hierarchy.PRESCRIBED, # 27 -> (0, 1, 1)
Hierarchy.BOUNDARY, # 28
Hierarchy.BOUNDARY, # 29
Hierarchy.BOUNDARY, # 30
Hierarchy.PRESCRIBED, # 31 -> (4.5*cos(15 deg), 4.5*sin(15 deg), 1)
Hierarchy.PRESCRIBED, # 32 -> *(0, 2, 1)
Hierarchy.BOUNDARY, # 33
Hierarchy.BOUNDARY, # 34
Hierarchy.BOUNDARY, # 35
Hierarchy.PRESCRIBED, # 36 -> (4.5*cos(30 deg), 4.5*sin(30 deg), 1)
Hierarchy.PRESCRIBED, # 37 -> (0, 3, 1)
Hierarchy.BOUNDARY, # 38
Hierarchy.BOUNDARY, # 39
Hierarchy.PRESCRIBED, # 40 -> (0, 4, 1)
Hierarchy.PRESCRIBED, # 41 -> (1.5, 4, 1)
Hierarchy.PRESCRIBED, # 42 -> (3.5, 4, 1)
)
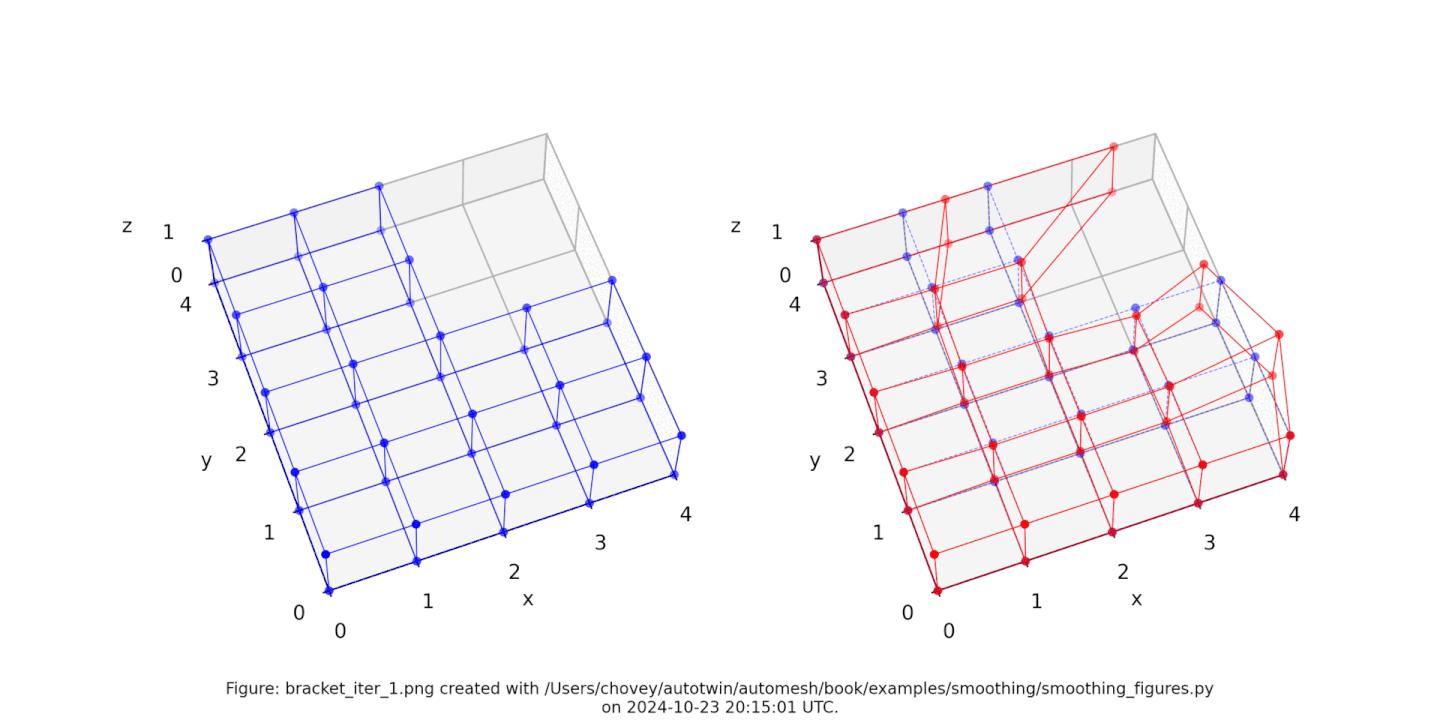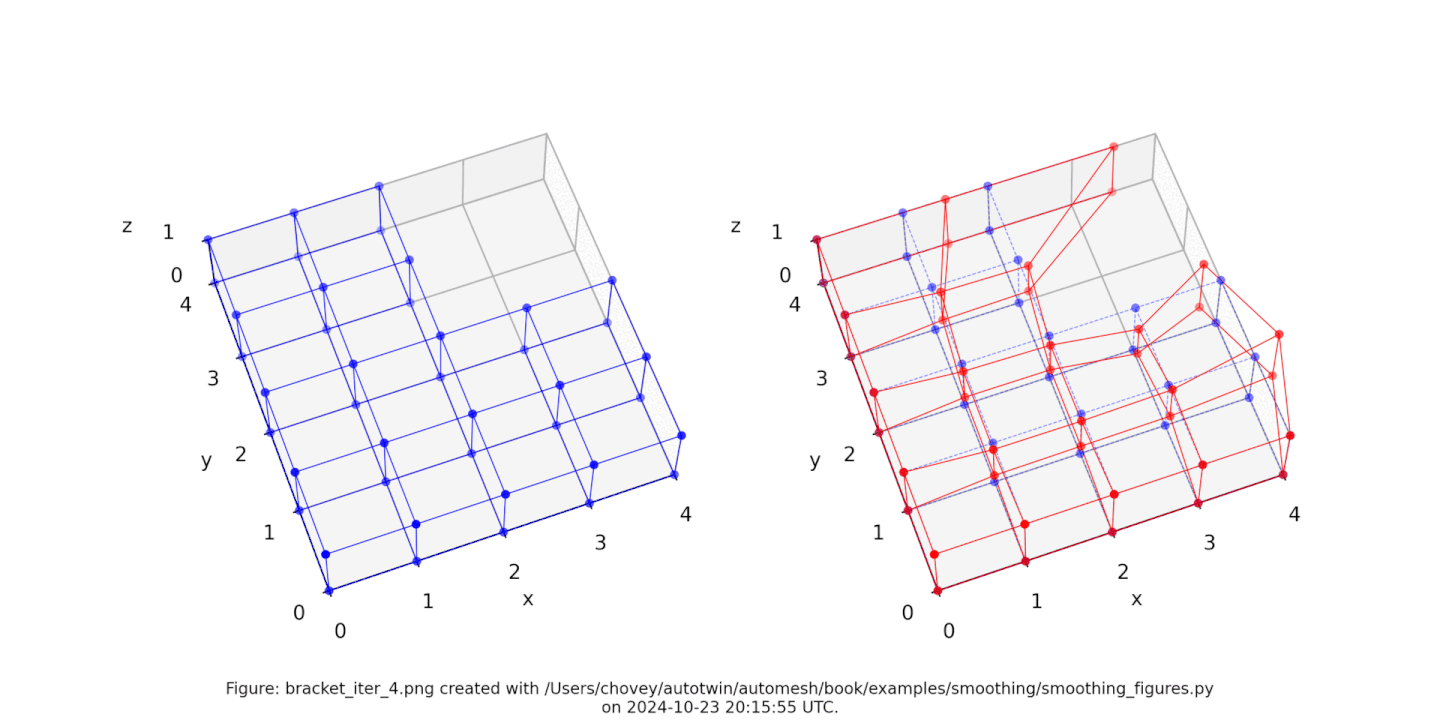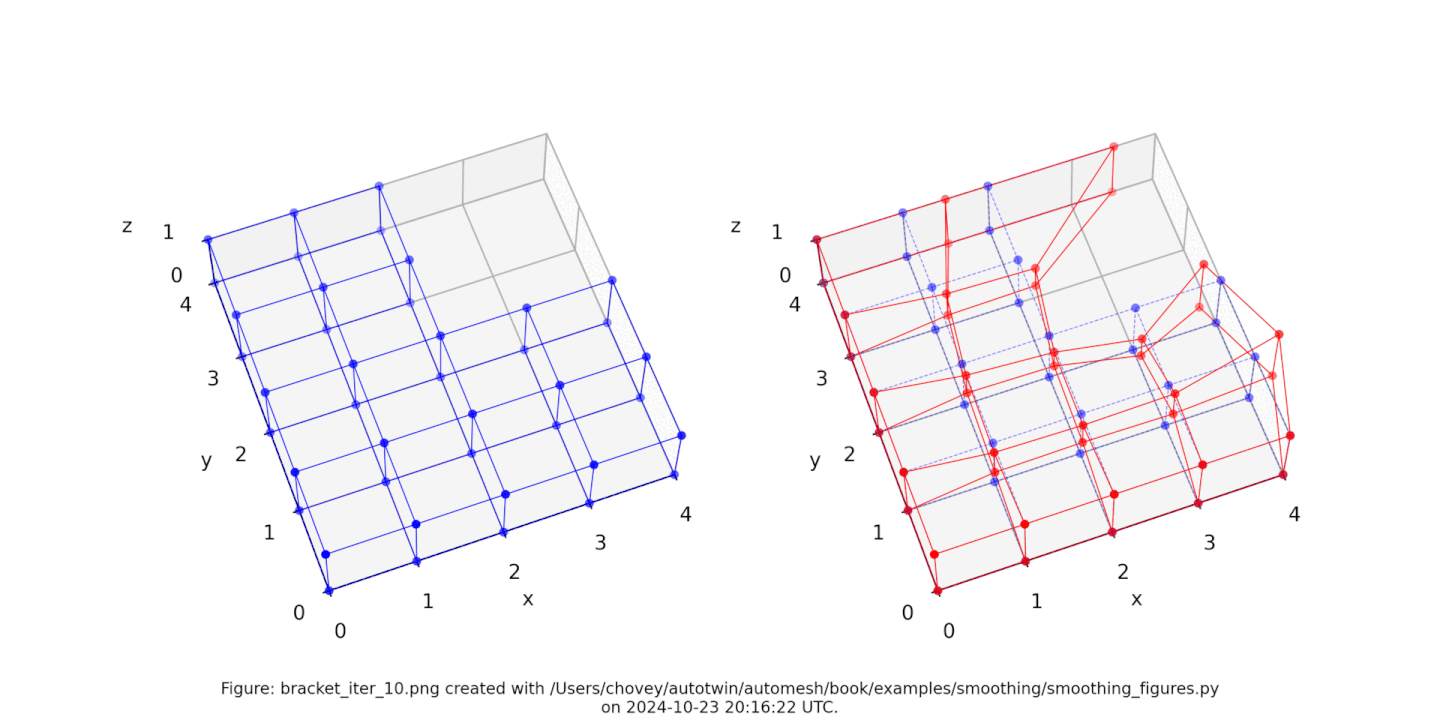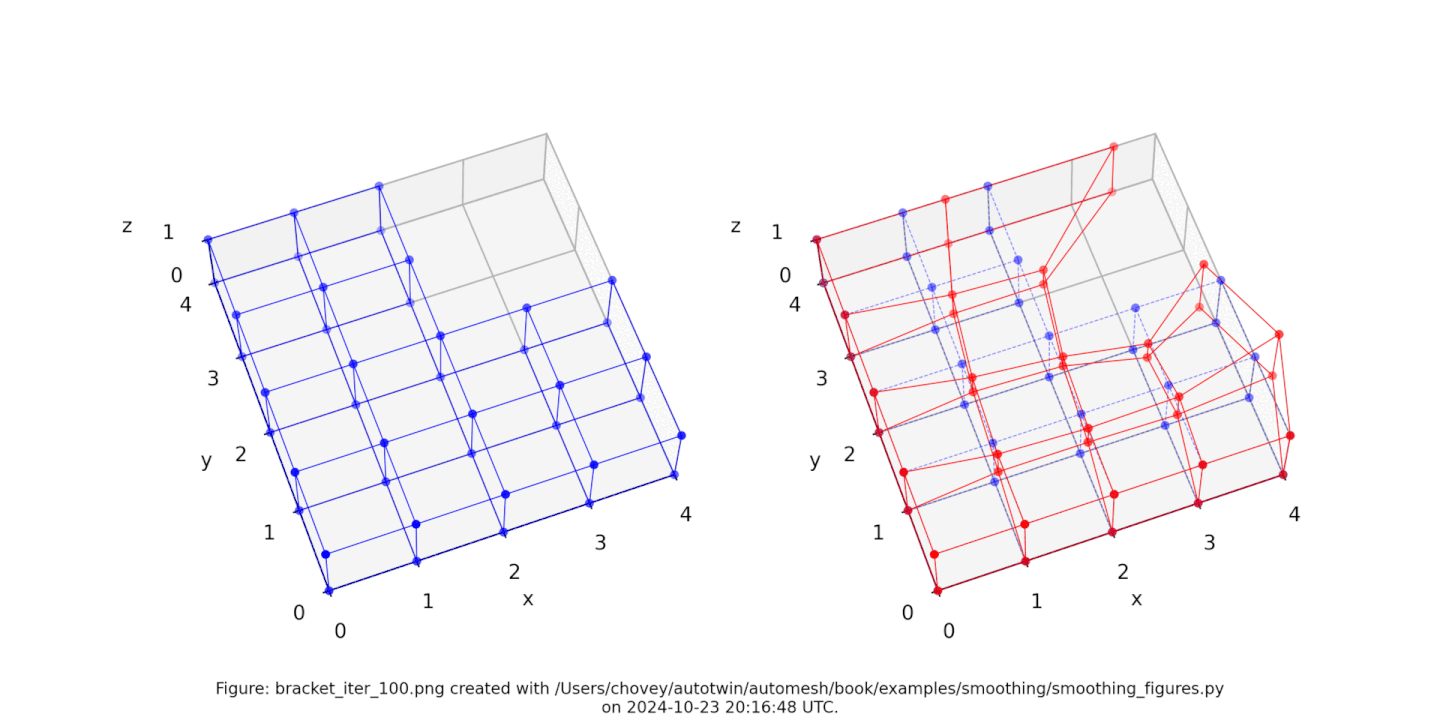
Figure: The Bracket test problem (left) original configuration, (right) subject to [1, 2, 3, 4, 5, 10, 20, 30, 100] iterations of Laplace smoothing with hierarchical control. Animation created with Ezgif.
As an example, the nodal positions after 10 iterations are as follows:
| node | x | y | z |
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| 2 | 1 | 0 | 0 |
| 3 | 2 | 0 | 0 |
| 4 | 3 | 0 | 0 |
| 5 | 4 | 0 | 0 |
| 6 | 0 | 1 | 0 |
| 7 | 1.0076218690550747 | 0.9988829259123082 | 0.24593434133370803 |
| 8 | 2.0218051968023 | 0.993985105791881 | 0.2837944855813176 |
| 9 | 3.0816593568068398 | 0.9931227966186256 | 0.24898414051620496 |
| 10 | 4.346666218300808 | 1.1646857029613433 | 0 |
| 11 | 0 | 2 | 0 |
| 12 | 1.0346002406957664 | 1.992982526945126 | 0.2837944855813176 |
| 13 | 2.0408618916639916 | 1.9528647520642073 | 0.3332231502067546 |
| 14 | 2.9955771790244468 | 1.7619821132207711 | 0.29909606343914835 |
| 15 | 3.897114317029974 | 2.2499999999999996 | 0 |
| 16 | 0 | 3 | 0 |
| 17 | 1.157261281731803 | 2.9982665159532105 | 0.24898414051620493 |
| 18 | 2.1973691292662734 | 2.991054895165017 | 0.29909606343914835 |
| 19 | 0 | 4 | 0 |
| 20 | 1.5 | 4 | 0 |
| 21 | 3.5 | 4 | 0 |
| 22 | 0 | 0 | 1 |
| 23 | 1 | 0 | 1 |
| 24 | 2 | 0 | 1 |
| 25 | 3 | 0 | 1 |
| 26 | 4 | 0 | 1 |
| 27 | 0 | 1 | 1 |
| 28 | 1.0076218690550747 | 0.9988829259123082 | 0.7540656586662919 |
| 29 | 2.0218051968023 | 0.993985105791881 | 0.7162055144186824 |
| 30 | 3.0816593568068398 | 0.9931227966186257 | 0.7510158594837951 |
| 31 | 4.346666218300808 | 1.1646857029613433 | 1 |
| 32 | 0 | 2 | 1 |
| 33 | 1.0346002406957664 | 1.9929825269451262 | 0.7162055144186824 |
| 34 | 2.0408618916639916 | 1.9528647520642073 | 0.6667768497932453 |
| 35 | 2.9955771790244468 | 1.7619821132207711 | 0.7009039365608517 |
| 36 | 3.897114317029974 | 2.2499999999999996 | 1 |
| 37 | 0 | 3 | 1 |
| 38 | 1.157261281731803 | 2.9982665159532105 | 0.751015859483795 |
| 39 | 2.1973691292662734 | 2.991054895165017 | 0.7009039365608516 |
| 40 | 0 | 4 | 1 |
| 41 | 1.5 | 4 | 1 |
| 42 | 3.5 | 4 | 1 |
Taubin Smoothing
We examine the Taubin smoothing algorithm on a sphere composed of hexahedral elements. We created a two block (green inner volume, yellow outer volume) mesh in Cubit, then added normal noise to the hemisphere where the coordinate was positive. We then applied Taubin smoothing to the noised model.
The Cubit and Python code used to generate the noised input file and figures is included below. Alternatively, the .inp files can be downloaded directly from the table below:
| name | size (MB) | md5 checksum |
|---|---|---|
sphere_res_1cm.inp | 1.5 | 644ef573c257222bfd61dcfda7131c6a |
sphere_res_1cm_noised.inp | 1.5 | 7031df475b972b15cf28bf2c5b69c162 |
The two-material sphere_res_1cm_noised.inp file is visualized below with and without a midplane cut.
| iso | iso midplane | xz midplane |
|---|---|---|
 |  |  |
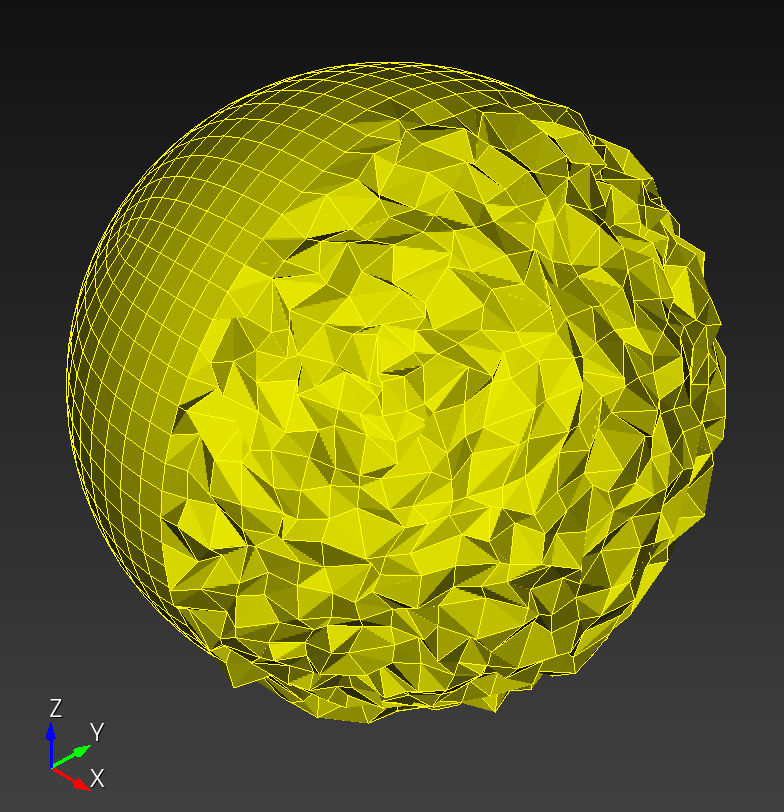 | 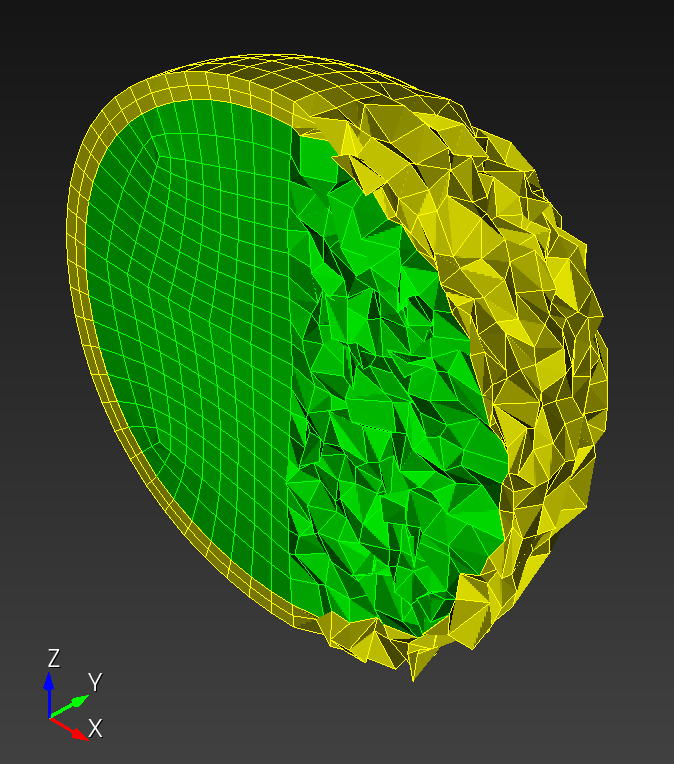 |  |
Figure: (Top row) sphere original configuration. (Bottom row) noised sphere configuration, with normal random nodal displacement of the coordinates where .
Taubin example

Figure: Excerpt from Taubin1, Figure 3, showing a surface mesh original configuration, and after 10, 50, and 200 steps.
automesh
We compare our volumetric results to the surface mesh presented by Taubin.1 A step is either a "shrinking step" (deflating, smoothing step) or an "un-shrinking step" (reinflating step).
The smoothing parameters used were the autotwin defaults,2 the same as used in Taubin's Figure 3 example.
automesh smooth hex -i sphere_res_1cm_noised.inp -o s10.exo -n 10
automesh smooth hex -i sphere_res_1cm_noised.inp -o s50.exo -n 50
automesh smooth hex -i sphere_res_1cm_noised.inp -o s200.exo -n 200
| front | iso | xz midplane |
|---|---|---|
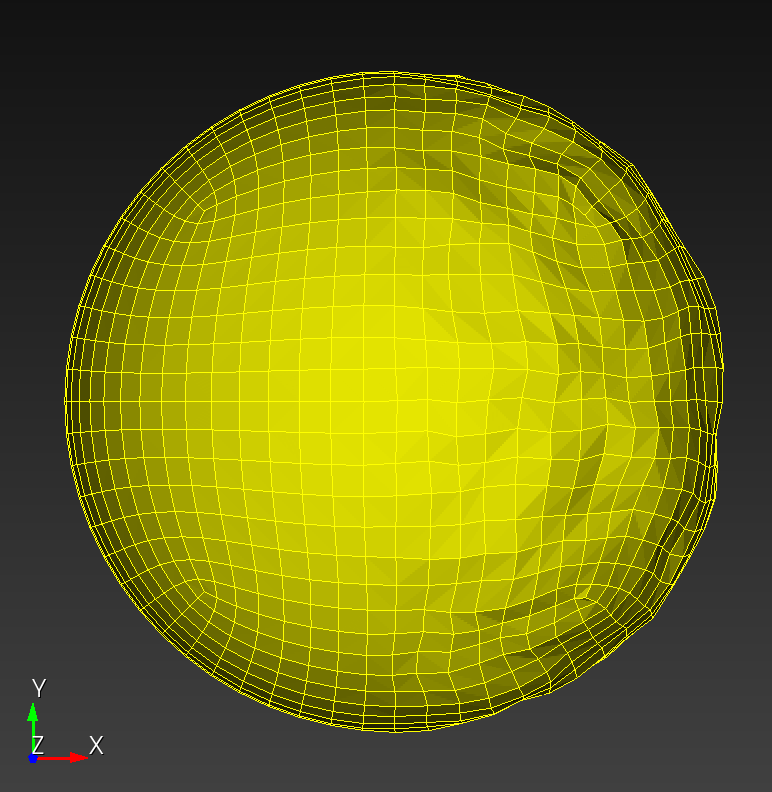 |  | 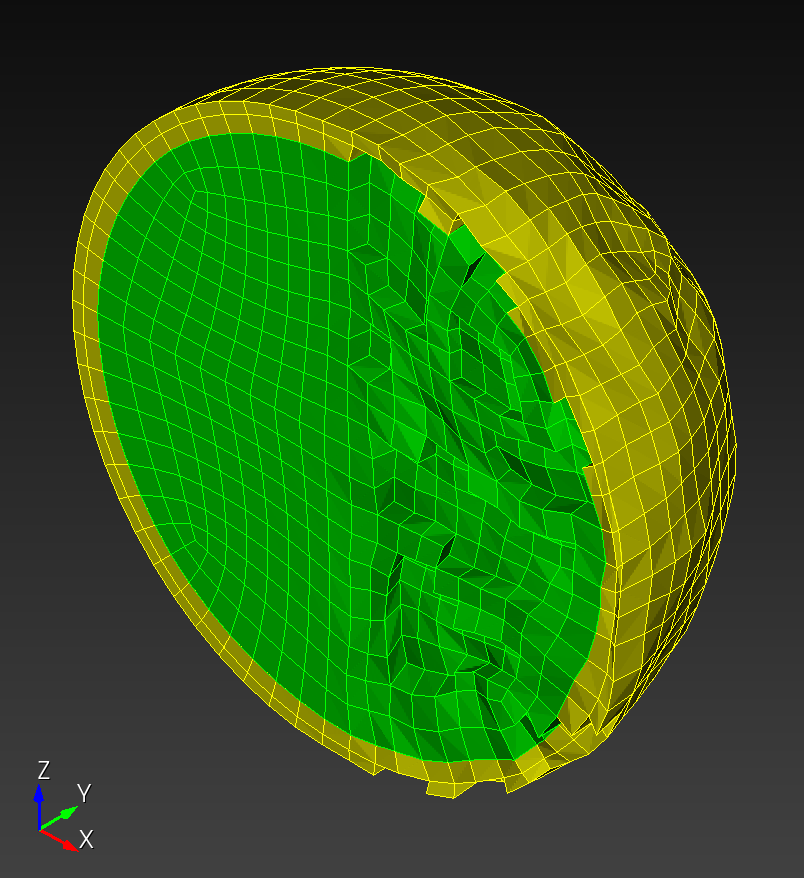 |
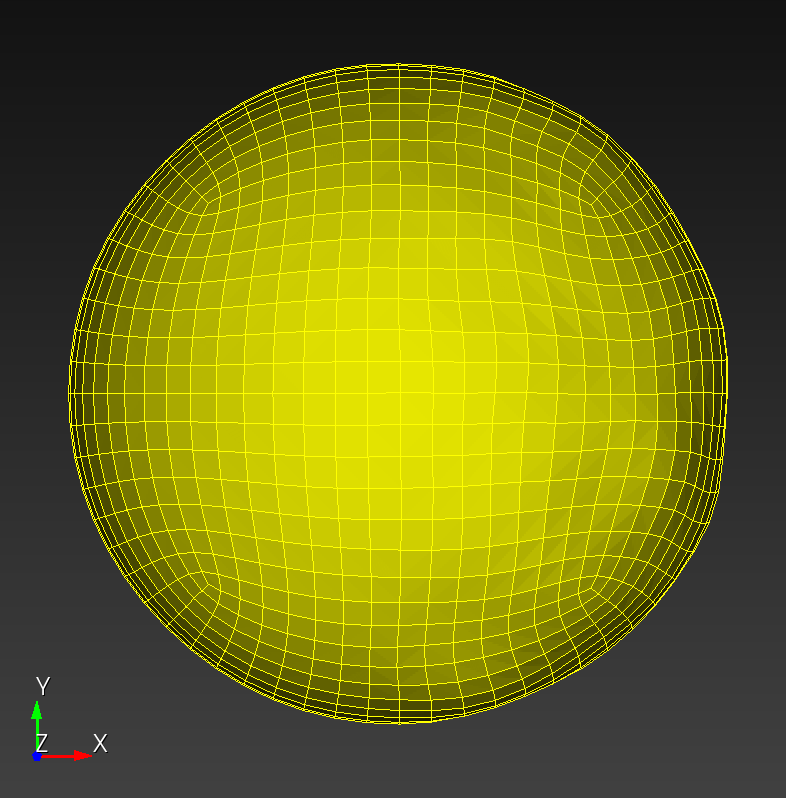 |  |  |
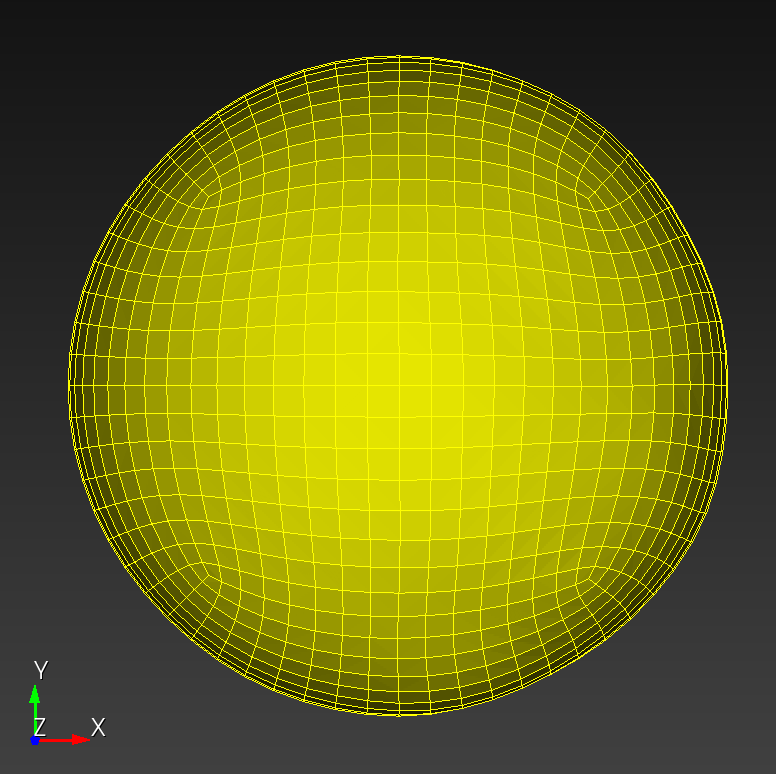 |  |  |
Figure. Smoothing results after 10 (top row), 50 (middle row), and 200 (bottom row) iterations.
The results demonstrate that our implementation of Taubin smoothing on volumetric meshes composed of hexahedral elements performs well. All smoothing operations completed within 7.5 ms. Unlike Laplace smoothing, which drastically reduces volume (e.g., -16% in 10 iterations), Taubin smoothing preserves volumes (e.g., +1% in 200 iterations). Thus, the noise in the hemisphere was effectively removed, with very small volumetric change. The hemisphere did not degrade from its original configuration.
Source
sphere.jou
# Cubit 16.14 on macOS
# automesh/book/smoothing/sphere.jou
reset
# ----------------
# INPUT PARAMETERS
# ----------------
# centimeters
# {INNER_RADIUS = 10.0} # cm
# {OUTER_RADIUS = 11.0} # cm
#
# {ELEMENT_SIZE = 1.0} # cm
#
# {UNITS = "cm"}
# {savefolder = "/Users/chovey/autotwin/basis/data/cubit/"}
# {savefolder = "/Users/chovey/autotwin/basis/scratch/"}
# {savefolder = "/Users/chovey/autotwin/automesh/book/smoothing/"}
# {basename = "sphere_res_"}
# {str_exodus = savefolder//basename//tostring(ELEMENT_SIZE)//UNITS//".e"}
# {str_exodus = savefolder//basename//tostring(ELEMENT_SIZE)//UNITS//".g"}
# example:
# /Users/chovey/autotwin/basis/data/cubit/spheres_e_len_0.01m.e
# /Users/chovey/autotwin/basis/data/cubit/spheres_e_len_0.01m.g
# /Users/chovey/autotwin/basis/scratch/smooth_1cm.g
# {str_abaqus = savefolder//basename//tostring(ELEMENT_SIZE)//UNITS//".inp"}
# example:
# /Users/chovey/autotwin/basis/data/cubit/spheres_e_len_0.01m.inp
# /Users/chovey/autotwin/basis/scratch/smooth_1cm.inp
# {str_export_exodus = 'export mesh "'//str_exodus// '" overwrite '}
# example:
# export mesh "/Users/chovey/autotwin/basis/data/cubit/spheres_e_len_0.01m.e" overwrite
# export mesh "/Users/chovey/autotwin/basis/data/cubit/spheres_e_len_0.01m.g" overwrite
# export mesh "/Users/chovey/autotwin/basis/scratch/smooth_1cm.g" overwrite
# {str_export_abaqus = 'export abaqus "'//str_abaqus// '" overwrite everything'}
# example:
# export abaqus "/Users/chovey/autotwin/basis/data/cubit/spheres_e_len_0.01m.inp" overwrite everything
# export abaqus "/Users/chovey/autotwin/basis/scratch/smooth_1cm.inp" overwrite everything
# From Sokolow, 2024-03-04-1725:
# // in aprepro is string concatenation
# I separated the folder from the file name just for readability.
# The definition of “st” is to setup the folder+filename
# The definition of “s2” is to prevent cubit/aprepro from getting confused with nested strings by using single quotes surrounding a solitary double quote.
# The last line “rescan” actually tells cubit to process the whole string as a command.
# The save folder definition I would put at the top of the journal file.
# -------------------
# DERIVED CALCUATIONS
# -------------------
# {OUTER_INTERVAL = max(2, ceil((OUTER_RADIUS - INNER_RADIUS)/ELEMENT_SIZE))}
# {ELEMENT_TOLERANCE = ELEMENT_SIZE/10000}
# {SELECTION_RADIUS = INNER_RADIUS/2.0}
create sphere radius {OUTER_RADIUS}
create sphere radius {INNER_RADIUS}
subtract volume 2 from volume 1 # creates new volume 3
create sphere radius {INNER_RADIUS} # creates new volume 4
section vol all yplane
section vol all zplane
section vol all xplane
imprint vol all
merge vol all
vol 4 rename "inner_vol"
vol 3 rename "outer_vol"
vol all size {ELEMENT_SIZE}
volume with name "inner_vol" scheme tetprimitive
# highlight curve with x_coord < 1.0 and with y_coord < 1.0 and with z_coord < 1.0
curve with x_coord < {SELECTION_RADIUS} and with y_coord < {SELECTION_RADIUS} and with z_coord < {SELECTION_RADIUS} interval {ceil(INNER_RADIUS/ELEMENT_SIZE)}
curve with x_coord < {SELECTION_RADIUS} and with y_coord < {SELECTION_RADIUS} and with z_coord < {SELECTION_RADIUS} scheme equal
mesh curve with x_coord < {SELECTION_RADIUS} and with y_coord < {SELECTION_RADIUS} and with z_coord < {SELECTION_RADIUS}
mesh volume with name "inner_vol"
curve 4 16 18 interval {OUTER_INTERVAL}
curve 4 16 18 scheme equal
mesh curve 4 16 18
volume with name "outer_vol" redistribute nodes off
# surface 19 is at the inner_vol radius
# surface 21 is at the outer_vol radius
volume with name "outer_vol" scheme sweep source surface 19 target surface 21 sweep transform least squares
volume with name "outer_vol" autosmooth target on fixed imprints off smart smooth off
mesh volume with name "outer_vol"
Volume all copy reflect x
imprint vol all
merge vol all
Volume all copy reflect y
imprint vol all
merge vol all
Volume all copy reflect z
imprint vol all
merge vol all
block 1 volume with name "inner_vol*"
block 2 volume with name "outer_vol*"
# quality volume all shape global draw mesh
# export mesh "/Users/chovey/autotwin/basis/data/cubit/unmerged" + {ELEMENT_SIZE}.e overwrite
# export mesh "/Users/chovey/autotwin/basis/data/cubit/unmerged.e" overwrite
# export mesh "/Users/chovey/autotwin/basis/scratch/unmerged.e" overwrite
export mesh "/Users/chovey/autotwin/automesh/book/smoothing/sphere_temp_unmerged.g" overwrite
reset
# import mesh geometry "/Users/chovey/autotwin/basis/data/cubit/unmerged.e" feature_angle 135.00 merge merge_nodes {ELEMENT_SIZE/100}
# import mesh geometry "/Users/chovey/autotwin/basis/data/cubit/unmerged.e" feature_angle 135.00 merge merge_nodes {ELEMENT_TOLERANCE}
# import mesh geometry "/Users/chovey/autotwin/basis/scratch/unmerged.e" feature_angle 135.00 merge merge_nodes {ELEMENT_TOLERANCE}
import mesh geometry "/Users/chovey/autotwin/automesh/book/smoothing/sphere_temp_unmerged.g" merge merge_nodes {ELEMENT_TOLERANCE}
sideset 1 add surface 1
sideset 2 add surface 2
# export mesh "/Users/chovey/autotwin/basis/scratch/smooth_1cm.g" overwrite
# export abaqus "/Users/chovey/autotwin/basis/scratch/smooth_1cm.inp" overwrite everything
# inner_vol = block 1: 7,168 elements
# outer_vol = block 2: 3,072 elements
# total: 10,240 elements
{rescan(str_export_exodus)}
{rescan(str_export_abaqus)}
# view iso
# graphics clip on plane xplane location 0 0 0 direction 0 0 1
graphics scale off
graphics scale on
graphics clip off
view iso
graphics clip on plane location 0 0 0 direction 0 1 0
view up 0 0 1
view from 100 -100 100
graphics clip manipulation off
view bottom
noise_augmentation.py
r"""This module, noise_augmentation.py, adds noise to a finite element mesh
in the .inp format.
Example:
--------
source ~/autotwin/automesh/.venv/bin/activate
cd ~/autotwin/automesh/book/smoothing
python noise_augmentation.py
"""
from pathlib import Path
from typing import Final
import random
FILE_INPUT: Final[Path] = Path(__file__).parent.joinpath("sphere_res_1cm.inp")
FILE_OUTPUT: Final[Path] = Path(__file__).parent.joinpath("sphere_res_1cm_noised.inp")
SEED_VALUE: Final[int] = 42 # set a seed value for reproducibility
random.seed(SEED_VALUE)
# AMP: Final[float] = 0.0 # the amplitude of the noise, debug
AMP: Final[float] = 0.5 # the amplitude of the noise
def has_e_plus_minus(string_in: str) -> bool:
"""Utility function, if the input string has the format
"E+", "e+", "E-", or "E-", then return True, otherwise False.
"""
return (
"E+" in string_in or "e+" in string_in or "E-" in string_in or "e-" in string_in
)
def has_four_entries(string_in: str) -> bool:
"""Utility function that evaluates a string. If the input has four
entries, which is the format of the nodal coordinates, then return
True, otherwise, return False."""
return len(string_in.split(",")) == 4
with (
open(FILE_INPUT, "r", encoding="utf-8") as fin,
open(FILE_OUTPUT, "w", encoding="utf-8") as fout,
):
for line in fin:
# print(line) # debugging
if has_four_entries(line):
# This might be a coordinate, investigate further.
items = line.split(",")
node, px, py, pz = tuple(i.strip() for i in items)
# if all coordinates have the E+/e+ or E-/e- notation
if all(has_e_plus_minus(k) for k in [px, py, pz]):
# we noise only coordinates on the positive x half-space
if float(px) > 0.0:
# Pick three random number between -1 and 1
rx = random.uniform(-1, 1)
ry = random.uniform(-1, 1)
rz = random.uniform(-1, 1)
# create the noise values
nx = AMP * rx
ny = AMP * ry
nz = AMP * rz
# create noisy values
qx = float(px) + nx
qy = float(py) + ny
qz = float(pz) + nz
formatted_line = (
f"{node:>8}, {qx:>15.6e}, {qy:>15.6e}, {qz:>15.6e}\n"
)
line = formatted_line # overwrite with new noised line
fout.write(line)
print(f"Wrote {FILE_OUTPUT}")
print("Done.")
References
-
Taubin G. A signal processing approach to fair surface design. In Proceedings of the 22nd annual conference on Computer graphics and interactive techniques 1995 Sep 15 (pp. 351-358). paper ↩ ↩2
-
autotwindefault Taubin parameters: , . ↩
Python Visualization
Following are files to support the Python visualization.
smoothing_types.py
r"""This module, smoothing_types.py, defines types used for smoothing
hexahedral meshes.
"""
from enum import Enum
from typing import NamedTuple
class Vertex(NamedTuple):
"""A general 3D vertex with x, y, and z coordinates."""
x: float
y: float
z: float
class Hierarchy(Enum):
"""All nodes must be categorized as beloning to one, and only one,
of the following hierarchical categories.
"""
INTERIOR = 0
BOUNDARY = 1
PRESCRIBED = 2
Vertices = tuple[Vertex, ...]
Hex = tuple[int, int, int, int, int, int, int, int] # only hex elements
Hexes = tuple[Hex, ...]
Neighbor = tuple[int, ...]
Neighbors = tuple[Neighbor, ...]
NodeHierarchy = tuple[Hierarchy, ...]
PrescribedNodes = tuple[tuple[int, Vertex], ...] | None
class SmoothingAlgorithm(Enum):
"""The type of smoothing algorithm."""
LAPLACE = "Laplace"
TAUBIN = "Taubin"
class SmoothingExample(NamedTuple):
"""The prototype smoothing example."""
vertices: Vertices
elements: Hexes
nelx: int
nely: int
nelz: int
# neighbors: Neighbors
node_hierarchy: NodeHierarchy
prescribed_nodes: PrescribedNodes
scale_lambda: float
scale_mu: float
num_iters: int
algorithm: SmoothingAlgorithm
file_stem: str
smoothing_test.py
r"""This module, smoothing_test.py, tests the smoothing modules.
Example:
--------
source ~/autotwin/automesh/.venv/bin/activate
cd ~/autotwin/automesh/book/examples/smoothing
python -m pytest smoothing_test.py
Reference:
----------
DoubleX unit test
https://autotwin.github.io/automesh/examples/unit_tests/index.html#double-x
"""
from typing import Final
# import sandbox.smoothing as sm
# import sandbox.smoothing_types as ty
import smoothing as sm
import smoothing_examples as examples
import smoothing_types as ty
# Type alias for functional style methods
# https://docs.python.org/3/library/typing.html#type-aliases
Hexes = ty.Hexes
Hierarchy = ty.Hierarchy
Neighbors = ty.Neighbors
NodeHierarchy = ty.NodeHierarchy
Vertex = ty.Vertex
Vertices = ty.Vertices
SmoothingAlgorithm = ty.SmoothingAlgorithm
def test_average_position():
"""Unit test for average_position"""
v1 = Vertex(x=1.0, y=2.0, z=3.0)
v2 = Vertex(x=4.0, y=5.0, z=6.0)
v3 = Vertex(x=7.0, y=8.0, z=9.0)
v_ave = sm.average_position((v1, v2, v3))
assert v_ave.x == 4.0
assert v_ave.y == 5.0
assert v_ave.z == 6.0
# docstring example
v1, v2 = Vertex(1, 2, 3), Vertex(4, 5, 6)
assert sm.average_position((v1, v2)) == Vertex(2.5, 3.5, 4.5)
def test_add():
"""Unit test for the addition of Vertex v1 and Vertex v2."""
v1 = Vertex(x=1.0, y=2.0, z=3.0)
v2 = Vertex(x=4.0, y=7.0, z=1.0)
vv = sm.add(v1=v1, v2=v2)
assert vv.x == 5.0
assert vv.y == 9.0
assert vv.z == 4.0
# docstring example
v1, v2 = Vertex(1, 2, 3), Vertex(4, 5, 6)
assert sm.add(v1, v2) == Vertex(5, 7, 9)
def test_subtract():
"""Unit test for the subtraction of Vertex v2 from Vertex v1."""
v1 = Vertex(x=1.0, y=2.0, z=3.0)
v2 = Vertex(x=4.0, y=7.0, z=1.0)
vv = sm.subtract(v1=v1, v2=v2)
assert vv.x == -3.0
assert vv.y == -5.0
assert vv.z == 2.0
# docstring example
v1, v2 = Vertex(8, 5, 2), Vertex(1, 2, 3)
assert sm.subtract(v1, v2) == Vertex(7, 3, -1)
def test_scale():
"""Unit test for the scale function."""
v1 = Vertex(x=1.0, y=2.0, z=3.0)
ss = 10.0
result = sm.scale(vertex=v1, scale_factor=ss)
assert result.x == 10.0
assert result.y == 20.0
assert result.z == 30.0
# docstring example
v = Vertex(1, 2, 3)
scale_factor = 2
assert sm.scale(v, scale_factor) == Vertex(2, 4, 6)
def test_xyz():
"""Unit test to assure the (x, y, z) coordinate tuple is returned
correctly.
"""
vv = Vertex(x=1.1, y=2.2, z=3.3)
gold = (1.1, 2.2, 3.3)
result = sm.xyz(vv)
assert result == gold
# docstring example
v = Vertex(1, 2, 3)
assert sm.xyz(v) == (1, 2, 3)
def test_smoothing_neighbors():
"""Given the Double X test problem with completely made up
node hierarchy, assure that `smoothing_neighbors` returns
the correct neighbors.
"""
ex = examples.double_x
# neighbors = ex.neighbors # borrow the neighbor connections
neighbors = sm.node_node_connectivity(ex.elements)
node_hierarchy = (
Hierarchy.INTERIOR,
Hierarchy.BOUNDARY,
Hierarchy.PRESCRIBED,
Hierarchy.PRESCRIBED,
Hierarchy.BOUNDARY,
Hierarchy.INTERIOR,
Hierarchy.INTERIOR,
Hierarchy.BOUNDARY,
Hierarchy.BOUNDARY,
Hierarchy.INTERIOR,
Hierarchy.INTERIOR,
Hierarchy.INTERIOR,
)
result = sm.smoothing_neighbors(neighbors=neighbors, node_hierarchy=node_hierarchy)
gold_smoothing_neighbors = (
(2, 4, 7),
(3, 5, 8),
(),
(),
(2, 4),
(3, 5, 12),
(1, 8, 10),
(2, 9),
(3, 8),
(4, 7, 11),
(5, 8, 10, 12),
(6, 9, 11),
)
assert result == gold_smoothing_neighbors
# doctring example
neighbors = ((2, 3), (1, 4), (1, 5), (2, 6), (3,), (4,))
node_hierarchy = (
Hierarchy.INTERIOR,
Hierarchy.BOUNDARY,
Hierarchy.PRESCRIBED,
Hierarchy.BOUNDARY,
Hierarchy.INTERIOR,
Hierarchy.INTERIOR,
)
gold = ((2, 3), (4,), (), (2,), (3,), (4,))
assert sm.smoothing_neighbors(neighbors, node_hierarchy) == gold
def test_laplace_hierarchical_bracket():
"""Unit test for Laplace smoothing with hierarhical control
on the Bracket example."""
bracket = examples.bracket
node_hierarchy = bracket.node_hierarchy
# neighbors = bracket.neighbors
neighbors = sm.node_node_connectivity(bracket.elements)
node_hierarchy = bracket.node_hierarchy
# If a node is PRESCRIBED, then it has no smoothing neighbors
smoothing_neighbors = sm.smoothing_neighbors(
neighbors=neighbors, node_hierarchy=node_hierarchy
)
gold_smoothing_neighbors = (
(), # 1
(), # 2
(), # 3
(), # 4
(), # 5
(), # 6
(2, 6, 8, 12, 28), # 7
(3, 7, 9, 13, 29), # 8
(4, 8, 10, 14, 30), # 9
(), # 10
(), # 11
(7, 11, 13, 17, 33), # 12
(8, 12, 14, 18, 34), # 13
(9, 13, 15, 35), # 14
(), # 15
(), # 16
(12, 16, 18, 20, 38), # 17
(13, 17, 21, 39), # 18
(), # 19
(), # 20
(),
(), # 22
(),
(), # 24
(),
(), # 26
(),
(7, 23, 27, 29, 33), # 28
(8, 24, 28, 30, 34), # 29
(9, 25, 29, 31, 35), # 30
(), # 31
(), # 32
(12, 28, 32, 34, 38), # 33
(13, 29, 33, 35, 39), # 34
(14, 30, 34, 36), # 35
(), # 36
(), # 37
(17, 33, 37, 39, 41), # 38
(18, 34, 38, 42), # 39
(), # 40
(), # 41
(), # 42
)
assert smoothing_neighbors == gold_smoothing_neighbors
# specific test with lambda = 0.3 and num_iters = 10
scale_lambda_test = 0.3
num_iters_test = 10
result = sm.smooth(
vv=bracket.vertices,
hexes=bracket.elements,
node_hierarchy=bracket.node_hierarchy,
prescribed_nodes=bracket.prescribed_nodes,
scale_lambda=scale_lambda_test,
num_iters=num_iters_test,
algorithm=bracket.algorithm,
)
gold_vertices_10_iter = (
Vertex(x=0, y=0, z=0),
Vertex(x=1, y=0, z=0),
Vertex(x=2, y=0, z=0),
Vertex(x=3, y=0, z=0),
Vertex(x=4, y=0, z=0),
Vertex(x=0, y=1, z=0),
Vertex(x=0.9974824535030984, y=0.9974824535030984, z=0.24593434133370803),
Vertex(x=1.9620726956646117, y=1.0109475009958278, z=0.2837944855813176),
Vertex(x=2.848322987789396, y=1.1190213008349328, z=0.24898414051620496),
Vertex(x=3.695518130045147, y=1.5307337294603591, z=0),
Vertex(x=0, y=2, z=0),
Vertex(x=1.0109475009958275, y=1.9620726956646117, z=0.2837944855813176),
Vertex(x=1.9144176939366933, y=1.9144176939366933, z=0.3332231502067546),
Vertex(x=2.5912759493290007, y=1.961874667390146, z=0.29909606343914835),
Vertex(x=2.8284271247461903, y=2.82842712474619, z=0),
Vertex(x=0, y=3, z=0),
Vertex(x=1.119021300834933, y=2.848322987789396, z=0.24898414051620493),
Vertex(x=1.9618746673901462, y=2.5912759493290007, z=0.29909606343914835),
Vertex(x=0, y=4, z=0),
Vertex(x=1.5307337294603593, y=3.695518130045147, z=0),
Vertex(x=2.8284271247461903, y=2.82842712474619, z=0),
Vertex(x=0, y=0, z=1),
Vertex(x=1, y=0, z=1),
Vertex(x=2, y=0, z=1),
Vertex(x=3, y=0, z=1),
Vertex(x=4, y=0, z=1),
Vertex(x=0, y=1, z=1),
Vertex(x=0.9974824535030984, y=0.9974824535030984, z=0.7540656586662919),
Vertex(x=1.9620726956646117, y=1.0109475009958278, z=0.7162055144186824),
Vertex(x=2.848322987789396, y=1.119021300834933, z=0.7510158594837951),
Vertex(x=3.695518130045147, y=1.5307337294603591, z=1),
Vertex(x=0, y=2, z=1),
Vertex(x=1.0109475009958275, y=1.9620726956646117, z=0.7162055144186824),
Vertex(x=1.9144176939366933, y=1.9144176939366933, z=0.6667768497932453),
Vertex(x=2.591275949329001, y=1.9618746673901462, z=0.7009039365608517),
Vertex(x=2.8284271247461903, y=2.82842712474619, z=1),
Vertex(x=0, y=3, z=1),
Vertex(x=1.1190213008349328, y=2.848322987789396, z=0.751015859483795),
Vertex(x=1.9618746673901462, y=2.5912759493290007, z=0.7009039365608516),
Vertex(x=0, y=4, z=1),
Vertex(x=1.5307337294603593, y=3.695518130045147, z=1),
Vertex(x=2.8284271247461903, y=2.82842712474619, z=1),
)
assert result == gold_vertices_10_iter
def test_laplace_smoothing_double_x():
"""Unit test for Laplace smoothing with all dofs as BOUNDARY
on the Double X example."""
vv: Vertices = (
Vertex(0.0, 0.0, 0.0),
Vertex(1.0, 0.0, 0.0),
Vertex(2.0, 0.0, 0.0),
Vertex(0.0, 1.0, 0.0),
Vertex(1.0, 1.0, 0.0),
Vertex(2.0, 1.0, 0.0),
Vertex(0.0, 0.0, 1.0),
Vertex(1.0, 0.0, 1.0),
Vertex(2.0, 0.0, 1.0),
Vertex(0.0, 1.0, 1.0),
Vertex(1.0, 1.0, 1.0),
Vertex(2.0, 1.0, 1.0),
)
hexes: Hexes = (
(1, 2, 5, 4, 7, 8, 11, 10),
(2, 3, 6, 5, 8, 9, 12, 11),
)
# nn: Neighbors = (
# (2, 4, 7),
# (1, 3, 5, 8),
# (2, 6, 9),
# (1, 5, 10),
# (2, 4, 6, 11),
# (3, 5, 12),
# (1, 8, 10),
# (2, 7, 9, 11),
# (3, 8, 12),
# (4, 7, 11),
# (5, 8, 10, 12),
# (6, 9, 11),
# )
nh: NodeHierarchy = (
Hierarchy.BOUNDARY,
Hierarchy.BOUNDARY,
Hierarchy.BOUNDARY,
Hierarchy.BOUNDARY,
Hierarchy.BOUNDARY,
Hierarchy.BOUNDARY,
Hierarchy.BOUNDARY,
Hierarchy.BOUNDARY,
Hierarchy.BOUNDARY,
Hierarchy.BOUNDARY,
Hierarchy.BOUNDARY,
Hierarchy.BOUNDARY,
)
scale_lambda: Final[float] = 0.3 # lambda for Laplace smoothing
# iteration 1
num_iters = 1 # single iteration of smoothing
algo = SmoothingAlgorithm.LAPLACE
aa = sm.smooth(
vv=vv,
hexes=hexes,
node_hierarchy=nh,
prescribed_nodes=None,
scale_lambda=scale_lambda,
num_iters=num_iters,
algorithm=algo,
)
cc: Final[float] = scale_lambda / 3.0 # delta corner
ee: Final[float] = scale_lambda / 4.0 # delta edge
# define the gold standard fiducial
gold = (
Vertex(x=cc, y=cc, z=cc), # node 1, corner
Vertex(x=1.0, y=ee, z=ee), # node 2, edge
Vertex(x=2.0 - cc, y=cc, z=cc), # node 3, corner
#
Vertex(x=cc, y=1.0 - cc, z=cc), # node 4, corner
Vertex(x=1.0, y=1.0 - ee, z=ee), # node 5, edge
Vertex(x=2.0 - cc, y=1.0 - cc, z=cc), # node 6, corner
#
Vertex(x=cc, y=cc, z=1 - cc), # node 7, corner
Vertex(x=1.0, y=ee, z=1 - ee), # node 8, edge
Vertex(x=2.0 - cc, y=cc, z=1 - cc), # node 9, corner
#
Vertex(x=cc, y=1.0 - cc, z=1 - cc), # node 10, corner
Vertex(x=1.0, y=1.0 - ee, z=1 - ee), # node 11, edge
Vertex(x=2.0 - cc, y=1.0 - cc, z=1 - cc), # node 12, corner
)
assert aa == gold
# iteration 2
num_iters = 2 # overwrite, double iteration of smoothing
aa2 = sm.smooth(
vv=vv,
hexes=hexes,
node_hierarchy=nh,
prescribed_nodes=None,
scale_lambda=scale_lambda,
num_iters=num_iters,
algorithm=algo,
)
# define the gold standard fiducial
gold2 = (
(0.19, 0.1775, 0.1775),
(1.0, 0.1425, 0.1425),
(1.8099999999999998, 0.1775, 0.1775),
(0.19, 0.8225, 0.1775),
(1.0, 0.8575, 0.1425),
(1.8099999999999998, 0.8225, 0.1775),
(0.19, 0.1775, 0.8225),
(1.0, 0.1425, 0.8575),
(1.8099999999999998, 0.1775, 0.8225),
(0.19, 0.8225, 0.8225),
(1.0, 0.8575, 0.8575),
(1.8099999999999998, 0.8225, 0.8225),
)
assert aa2 == gold2
def test_pair_ordered():
"""Unit test for pair ordered."""
# small toy example
given = ((3, 1), (2, 1))
found = sm.pair_ordered(given)
gold = ((1, 2), (1, 3))
assert found == gold
# example from 12 edges of a hex element
given = (
(1, 2),
(2, 5),
(4, 1),
(5, 4),
(7, 8),
(8, 11),
(11, 10),
(10, 7),
(1, 7),
(2, 8),
(5, 11),
(4, 10),
) # overwrite
gold = (
(1, 2),
(1, 4),
(1, 7),
(2, 5),
(2, 8),
(4, 5),
(4, 10),
(5, 11),
(7, 8),
(7, 10),
(8, 11),
(10, 11),
) # overwrite
found = sm.pair_ordered(given) # overwrite
assert found == gold
# docstring example
pairs = ((3, 1), (2, 4), (5, 0))
assert sm.pair_ordered(pairs) == ((0, 5), (1, 3), (2, 4))
def test_edge_pairs():
"""Units test to assure edge pairs are computed correctly."""
elements = (
(1, 2, 5, 4, 7, 8, 11, 10),
(2, 3, 6, 5, 8, 9, 12, 11),
)
found = sm.edge_pairs(hexes=elements)
gold = (
(1, 2),
(1, 4),
(1, 7),
(2, 3),
(2, 5),
(2, 8),
(3, 6),
(3, 9),
(4, 5),
(4, 10),
(5, 6),
(5, 11),
(6, 12),
(7, 8),
(7, 10),
(8, 9),
(8, 11),
(9, 12),
(10, 11),
(11, 12),
)
assert found == gold
def test_node_node_connectivity():
"""Tests that the node_node_connectivity function is properly
implemented.
"""
# from the Double X unit test
hexes = (
(1, 2, 5, 4, 7, 8, 11, 10),
(2, 3, 6, 5, 8, 9, 12, 11),
)
gold_neighbors = (
(2, 4, 7),
(1, 3, 5, 8),
(2, 6, 9),
(1, 5, 10),
(2, 4, 6, 11),
(3, 5, 12),
(1, 8, 10),
(2, 7, 9, 11),
(3, 8, 12),
(4, 7, 11),
(5, 8, 10, 12),
(6, 9, 11),
)
result = sm.node_node_connectivity(hexes)
assert gold_neighbors == result
# now with node number modifications to assure the
# algorithm does not assume sequential node numbers:
# 2 -> 22
# 5 -> 55
# 8 -> 88
# 11 -> 111
hexes_2 = (
(1, 22, 55, 4, 7, 88, 111, 10),
(22, 3, 6, 55, 88, 9, 12, 111),
)
gold_neighbors_2 = (
(4, 7, 22), # 1
(6, 9, 22), # 3
(1, 10, 55), # 4
(3, 12, 55), # 6
(1, 10, 88), # 7
(3, 12, 88), # 9
(4, 7, 111), # 10
(6, 9, 111), # 12
(1, 3, 55, 88), # 2 -> 22
(4, 6, 22, 111), # 5 -> 55
(7, 9, 22, 111), # 8 -> 88
(10, 12, 55, 88), # 11 -> 111
)
result_2 = sm.node_node_connectivity(hexes_2)
assert gold_neighbors_2 == result_2
# example from the L-bracket example
hexes_bracket = (
(1, 2, 7, 6, 22, 23, 28, 27),
(2, 3, 8, 7, 23, 24, 29, 28),
(3, 4, 9, 8, 24, 25, 30, 29),
(4, 5, 10, 9, 25, 26, 31, 30),
(6, 7, 12, 11, 27, 28, 33, 32),
(7, 8, 13, 12, 28, 29, 34, 33),
(8, 9, 14, 13, 29, 30, 35, 34),
(9, 10, 15, 14, 30, 31, 36, 35),
(11, 12, 17, 16, 32, 33, 38, 37),
(12, 13, 18, 17, 33, 34, 39, 38),
(16, 17, 20, 19, 37, 38, 41, 40),
(17, 18, 21, 20, 38, 39, 42, 41),
)
gold_neighbors_bracket = (
(2, 6, 22),
(1, 3, 7, 23),
(2, 4, 8, 24),
(3, 5, 9, 25),
(4, 10, 26),
#
(1, 7, 11, 27),
(2, 6, 8, 12, 28),
(3, 7, 9, 13, 29),
(4, 8, 10, 14, 30),
(5, 9, 15, 31),
#
(6, 12, 16, 32),
(7, 11, 13, 17, 33),
(8, 12, 14, 18, 34),
(9, 13, 15, 35),
(10, 14, 36),
#
(11, 17, 19, 37),
(12, 16, 18, 20, 38),
(13, 17, 21, 39),
#
(16, 20, 40),
(17, 19, 21, 41),
(18, 20, 42),
# top layer
(1, 23, 27),
(2, 22, 24, 28),
(3, 23, 25, 29),
(4, 24, 26, 30),
(5, 25, 31),
#
(6, 22, 28, 32),
(7, 23, 27, 29, 33),
(8, 24, 28, 30, 34),
(9, 25, 29, 31, 35),
(10, 26, 30, 36),
#
(11, 27, 33, 37),
(12, 28, 32, 34, 38),
(13, 29, 33, 35, 39),
(14, 30, 34, 36),
(15, 31, 35),
#
(16, 32, 38, 40),
(17, 33, 37, 39, 41),
(18, 34, 38, 42),
#
(19, 37, 41),
(20, 38, 40, 42),
(21, 39, 41),
)
result_bracket = sm.node_node_connectivity(hexes_bracket)
assert gold_neighbors_bracket == result_bracket
smoothing.py
r"""This module, smoothing.py, contains the core computations for
smoothing algorithms.
"""
# import sandbox.smoothing_types as ty
import smoothing_types as ty
# Type alias for functional style methods
# https://docs.python.org/3/library/typing.html#type-aliases
Hexes = ty.Hexes
Hierarchy = ty.Hierarchy
Neighbors = ty.Neighbors
NodeHierarchy = ty.NodeHierarchy
PrescribedNodes = ty.PrescribedNodes
Vertex = ty.Vertex
Vertices = ty.Vertices
SmoothingAlgorithm = ty.SmoothingAlgorithm
def average_position(vertices: Vertices) -> Vertex:
"""Calculate the average position of a list of vertices.
This function computes the average coordinates (x, y, z) of a given
list of Vertex objects. It raises an assertion error if the input
list is empty.
Parameters:
vertices (Vertices): A list or collection of Vertex objects, where
each Vertex has x, y, and z attributes
representing its coordinates in 3D space.
Returns:
Vertex: A new Vertex object representing the average position of the
input vertices, with x, y, and z attributes set to the
average coordinates.
Raises:
AssertionError: If the number of vertices is zero, indicating that
the input list must contain at least one vertex.
Example:
>>> v1 = Vertex(1, 2, 3)
>>> v2 = Vertex(4, 5, 6)
>>> average_position([v1, v2])
Vertex(x=2.5, y=3.5, z=4.5)
"""
n_vertices = len(vertices)
assert n_vertices > 0, "Error: number of vertices must be positive."
xs = [v.x for v in vertices]
ys = [v.y for v in vertices]
zs = [v.z for v in vertices]
x_ave = sum(xs) / n_vertices
y_ave = sum(ys) / n_vertices
z_ave = sum(zs) / n_vertices
return Vertex(x=x_ave, y=y_ave, z=z_ave)
def add(v1: Vertex, v2: Vertex) -> Vertex:
"""
Add two Vertex objects component-wise.
This function takes two Vertex objects and returns a new Vertex
object that represents the component-wise addition of the two
input vertices.
Parameters:
v1 (Vertex): The first Vertex object to be added.
v2 (Vertex): The second Vertex object to be added.
Returns:
Vertex: A new Vertex object representing the result of the addition,
with x, y, and z attributes set to the sum of the corresponding
attributes of v1 and v2.
Example:
>>> v1 = Vertex(1, 2, 3)
>>> v2 = Vertex(4, 5, 6)
>>> add(v1, v2)
Vertex(x=5, y=7, z=9)
"""
dx = v1.x + v2.x
dy = v1.y + v2.y
dz = v1.z + v2.z
return Vertex(x=dx, y=dy, z=dz)
def subtract(v1: Vertex, v2: Vertex) -> Vertex:
"""
Subtract one Vertex object from another component-wise.
This function takes two Vertex objects and returns a new Vertex
object that represents the component-wise subtraction of the second
vertex from the first.
Parameters:
v1 (Vertex): The Vertex object from which v2 will be subtracted.
v2 (Vertex): The Vertex object to be subtracted from v1.
Returns:
Vertex: A new Vertex object representing the result of the subtraction,
(v1 - v2), with x, y, and z attributes set to the difference
of the corresponding attributes of v1 and v2.
Example:
>>> v1 = Vertex(8, 5, 2)
>>> v2 = Vertex(1, 2, 3)
>>> subtract(v1, v2)
Vertex(x=7, y=3, z=-1)
"""
dx = v1.x - v2.x
dy = v1.y - v2.y
dz = v1.z - v2.z
return Vertex(x=dx, y=dy, z=dz)
def scale(vertex: Vertex, scale_factor: float) -> Vertex:
"""
Scale a Vertex object by a given scale factor.
This function takes a Vertex object and a scale factor, and returns
a new Vertex object that represents the original vertex scaled by
the specified factor.
Parameters:
vertex (Vertex): The Vertex object to be scaled.
scale_factor (float): The factor by which to scale the vertex.
This can be any real number, including
positive, negative, or zero.
Returns:
Vertex: A new Vertex object representing the scaled vertex, with
x, y, and z attributes set to the original coordinates
multiplied by the scale factor.
Example:
>>> v = Vertex(1, 2, 3)
>>> scale_factor = 2
>>> scale(v, scale_factor)
Vertex(x=2, y=4, z=6)
"""
x = scale_factor * vertex.x
y = scale_factor * vertex.y
z = scale_factor * vertex.z
return Vertex(x=x, y=y, z=z)
def xyz(v1: Vertex) -> tuple[float, float, float]:
"""
Extract the coordinates of a Vertex object.
This function takes a Vertex object and returns its coordinates
as a tuple in the form (x, y, z).
Parameters:
v1 (Vertex): The Vertex object from which to extract the coordinates.
Returns:
tuple[float, float, float]: A tuple containing the x, y, and z
coordinates of the vertex.
Example:
>>> v = Vertex(1, 2, 3)
>>> xyz(v)
(1, 2, 3)
"""
aa, bb, cc = v1.x, v1.y, v1.z
return (aa, bb, cc)
def smoothing_neighbors(neighbors: Neighbors, node_hierarchy: NodeHierarchy):
"""
Determine the smoothing neighbors for each node based on its
hierarchy level.
This function takes an original neighbors structure, which is defined
by the connectivity of a mesh, and a node hierarchy. It returns a
subset of the original neighbors that are used for smoothing, based
on the hierarchy levels of the nodes.
Parameters:
neighbors (Neighbors): A structure containing the original neighbors
for each node in the mesh.
node_hierarchy (NodeHierarchy): A structure that defines the hierarchy
levels of the nodes, which can be
INTERIOR, BOUNDARY, or PRESCRIBED.
Returns:
tuple: A new structure containing the neighbors used for smoothing,
which is a subset of the original neighbors based on the
hierarchy levels.
Raises:
ValueError: If a hierarchy value is not in the expected range
of [INTERIOR, BOUNDAR, PRESCRIBED, or [0, 1, 2],
respectively.
Example:
INTERIOR PRESCRIBED INTERIOR
(1) -------- (3) ----------- (5)
|
(2) -------- (4) ----------- (6)
BOUNDARY BOUNDARY INTERIOR
>>> neighbors = ((2, 3), (1, 4), (1, 5), (2, 6), (3,), (4,))
>>> node_hierarchy = (Hierarchy.INTERIOR, Hierarchy.BOUNDARY,
Hierarchy.PRESCRIBED, Hierarchy.BOUNDARY,
Hierarchy.INTERIOR, Hierarchy.INTERIOR)
>>> smoothing_neighbors(neighbors, node_hierarchy)
((2, 3), (4,), (), (2,), (3,), (4,))
"""
neighbors_new = ()
for node, level in enumerate(node_hierarchy):
nei_old = neighbors[node]
# print(f"Processing node {node+1}, neighbors: {nei_old}")
levels = [int(node_hierarchy[x - 1].value) for x in nei_old]
nei_new = ()
# breakpoint()
if level == Hierarchy.INTERIOR:
# print("INTERIOR node")
nei_new = nei_old
elif level == Hierarchy.BOUNDARY:
# print("BOUNDARY node")
for nn, li in zip(nei_old, levels):
if li >= level.value:
nei_new += (nn,)
elif level == Hierarchy.PRESCRIBED:
# print("PRESCRIBED node")
nei_new = ()
else:
raise ValueError("Hierarchy value must be in [0, 1, 2]")
neighbors_new += (nei_new,)
return neighbors_new
def smooth(
vv: Vertices,
hexes: Hexes,
node_hierarchy: NodeHierarchy,
prescribed_nodes: PrescribedNodes,
scale_lambda: float,
num_iters: int,
algorithm: SmoothingAlgorithm,
) -> Vertices:
"""
Given an initial position of vertices, the vertex neighbors,
and the dof classification of each vertex, perform Laplace
smoothing for num_iter iterations, and return the updated
coordinates.
"""
print(f"Smoothing algorithm: {algorithm.value}")
assert num_iters >= 1, "`num_iters` must be 1 or greater"
nn = node_node_connectivity(hexes)
# if the node_hierarchy contains a Hierarchy.PRESCRIBED type; or
# the the PrescribedNodes must not be None
if Hierarchy.PRESCRIBED in node_hierarchy:
info = "Smoothing algorithm with hierarchical control"
info += " and PRESCRIBED node positions."
print(info)
estr = "Error, NodeHierarchy desigates PRESCRIBED nodes, but no values"
estr += " for (x, y, z) prescribed positions were given."
assert prescribed_nodes is not None, estr
n_nodes_prescribed = node_hierarchy.count(Hierarchy.PRESCRIBED)
n_prescribed_xyz = len(prescribed_nodes)
estr = f"Error: number of PRESCRIBED nodes: {n_nodes_prescribed}"
estr += " must match the number of"
estr += f" prescribed Vertices(x, y, z): {n_prescribed_xyz}"
assert n_nodes_prescribed == n_prescribed_xyz, estr
# update neighbors
nn = smoothing_neighbors(
neighbors=nn, node_hierarchy=node_hierarchy
) # overwrite
# update vertex positions
vv_list = list(vv) # make mutable
for node_id, node_xyz in prescribed_nodes:
# print(f"Update node {node_id}")
# print(f" from {vv_list[node_id-1]}")
# print(f" to {node_xyz}")
vv_list[node_id - 1] = node_xyz # zero index, overwrite xyz
# revert to immutable
vv = tuple(vv_list) # overwrite
vertices_old = vv
# breakpoint()
for k in range(num_iters):
print(f"Iteration: {k + 1}")
vertices_new = []
for vertex, neighbors in zip(vertices_old, nn):
# debug vertex by vertex
# print(f"vertex {vertex}, neighbors {neighbors}")
# account for zero-index instead of 1-index:
neighbor_vertices = tuple(
vertices_old[i - 1] for i in neighbors
) # zero index
if len(neighbor_vertices) > 0:
neighbor_average = average_position(neighbor_vertices)
delta = subtract(v1=neighbor_average, v2=vertex)
lambda_delta = scale(vertex=delta, scale_factor=scale_lambda)
vertex_new = add(v1=vertex, v2=lambda_delta)
elif len(neighbor_vertices) == 0:
# print("Prescribed node, no smoothing update.")
vertex_new = vertex
else:
estr = "Error: neighbor_vertices negative length"
raise ValueError(estr)
vertices_new.append(vertex_new)
# breakpoint()
vertices_old = vertices_new # overwrite for new k loop
# breakpoint()
return tuple(vertices_new)
def pair_ordered(ab: tuple[tuple[int, int], ...]) -> tuple:
"""
Order pairs of integers based on their values.
Given a tuple of pairs in the form ((a, b), (c, d), ...), this
function orders each pair such that the smaller integer comes
first. It then sorts the resulting pairs primarily by the first
element and secondarily by the second element.
Parameters:
ab (tuple[tuple[int, int], ...]): A tuple containing pairs of integers.
Returns:
tuple: A new tuple containing the ordered pairs, where each pair
is sorted internally and the entire collection is sorted
based on the first and second elements.
Example:
>>> pairs = ((3, 1), (2, 4), (5, 0))
>>> pair_ordered(pairs)
((0, 5), (1, 3), (2, 4))
"""
firsts, seconds = zip(*ab)
ab_ordered = ()
for a, b in zip(firsts, seconds):
if a < b:
ab_ordered += ((a, b),)
else:
ab_ordered += ((b, a),)
# for a in firsts:
# print(f"a = {a}")
# for b in seconds:
# print(f"b = {b}")
result = tuple(sorted(ab_ordered))
return result
def edge_pairs(hexes: Hexes):
"""
Extract unique edge pairs from hex element connectivity.
This function takes a collection of hex elements and returns all
unique line pairs that represent the edges of the hex elements.
The edges are derived from the connectivity of the hex elements,
including both the horizontal edges (bottom and top faces) and
the vertical edges.
Used for drawing edges of finite elements.
Parameters:
hexes (Hexes): A collection of hex elements, where each hex is
represented by a tuple of vertex indices.
Returns:
tuple: A sorted tuple of unique edge pairs, where each pair is
represented as a tuple of two vertex indices.
"""
pairs = ()
for ee in hexes:
# bottom_face = tuple(sorted(list(zip(ee[0:4], ee[1:4] + (ee[0],)))))
bottom_face = pair_ordered(tuple(zip(ee[0:4], ee[1:4] + (ee[0],))))
# top_face = tuple(list(zip(ee[4:8], ee[5:8] + (ee[4],))))
top_face = pair_ordered(tuple(zip(ee[4:8], ee[5:8] + (ee[4],))))
verticals = pair_ordered(
(
(ee[0], ee[4]),
(ee[1], ee[5]),
(ee[2], ee[6]),
(ee[3], ee[7]),
)
)
t3 = bottom_face + top_face + verticals
pairs = pairs + tuple(t3)
# breakpoint()
return tuple(sorted(set(pairs)))
def node_node_connectivity(hexes: Hexes) -> Neighbors:
"""
Determine the connectivity of nodes to other nodes from
a list of hexahedral elements.
This function takes a list of hexahedral elements and returns a
list of nodes connected to each node based on the edges define
by the hexahedral elements. Each node's connectivity is represented
as a tuple of neighboring nodes.
Parameters:
hexes (Hexes): A collection of hexahedral elements, where each
element is represented by a tuple of node indices.
Returns:
Neighbors: A tuple of tuples, where each inner tuple contains the
indices of nodes connected to the corresponding node
in the input list.
"""
# create an empty dictionary from the node numbers
edict = {item: () for sublist in hexes for item in sublist}
ep = edge_pairs(hexes)
for edge in ep:
aa, bb = edge
# existing value at edict[a] is a_old
a_old = edict[aa]
# existing value at edict[b] is b_old
b_old = edict[bb]
# new value
a_new = (bb,)
b_new = (aa,)
# update dictionary
edict[aa] = a_old + a_new
edict[bb] = b_old + b_new
# create a new dictionary, sorted by keys
sorted_edict = dict(sorted(edict.items()))
neighbors = tuple(sorted_edict.values())
return neighbors
smoothing_examples.py
r"""This module, smoothing_examples.py contains data for the
smoothing examples.
"""
import math
from typing import Final
import smoothing_types as ty
# Type alias for functional style methods
# https://docs.python.org/3/library/typing.html#type-aliases
Hierarchy = ty.Hierarchy
SmoothingAlgorithm = ty.SmoothingAlgorithm
Example = ty.SmoothingExample
Vertex = ty.Vertex
DEG2RAD: Final[float] = math.pi / 180.0 # rad/deg
# L-bracket example
bracket = Example(
vertices=(
Vertex(0, 0, 0),
Vertex(1, 0, 0),
Vertex(2, 0, 0),
Vertex(3, 0, 0),
Vertex(4, 0, 0),
Vertex(0, 1, 0),
Vertex(1, 1, 0),
Vertex(2, 1, 0),
Vertex(3, 1, 0),
Vertex(4, 1, 0),
Vertex(0, 2, 0),
Vertex(1, 2, 0),
Vertex(2, 2, 0),
Vertex(3, 2, 0),
Vertex(4, 2, 0),
Vertex(0, 3, 0),
Vertex(1, 3, 0),
Vertex(2, 3, 0),
Vertex(0, 4, 0),
Vertex(1, 4, 0),
Vertex(2, 4, 0),
Vertex(0, 0, 1),
Vertex(1, 0, 1),
Vertex(2, 0, 1),
Vertex(3, 0, 1),
Vertex(4, 0, 1),
Vertex(0, 1, 1),
Vertex(1, 1, 1),
Vertex(2, 1, 1),
Vertex(3, 1, 1),
Vertex(4, 1, 1),
Vertex(0, 2, 1),
Vertex(1, 2, 1),
Vertex(2, 2, 1),
Vertex(3, 2, 1),
Vertex(4, 2, 1),
Vertex(0, 3, 1),
Vertex(1, 3, 1),
Vertex(2, 3, 1),
Vertex(0, 4, 1),
Vertex(1, 4, 1),
Vertex(2, 4, 1),
),
elements=(
(1, 2, 7, 6, 22, 23, 28, 27),
(2, 3, 8, 7, 23, 24, 29, 28),
(3, 4, 9, 8, 24, 25, 30, 29),
(4, 5, 10, 9, 25, 26, 31, 30),
(6, 7, 12, 11, 27, 28, 33, 32),
(7, 8, 13, 12, 28, 29, 34, 33),
(8, 9, 14, 13, 29, 30, 35, 34),
(9, 10, 15, 14, 30, 31, 36, 35),
(11, 12, 17, 16, 32, 33, 38, 37),
(12, 13, 18, 17, 33, 34, 39, 38),
(16, 17, 20, 19, 37, 38, 41, 40),
(17, 18, 21, 20, 38, 39, 42, 41),
),
nelx=4,
nely=4,
nelz=1,
# neighbors=(
# (2, 6, 22),
# (1, 3, 7, 23),
# (2, 4, 8, 24),
# (3, 5, 9, 25),
# (4, 10, 26),
# #
# (1, 7, 11, 27),
# (2, 6, 8, 12, 28),
# (3, 7, 9, 13, 29),
# (4, 8, 10, 14, 30),
# (5, 9, 15, 31),
# #
# (6, 12, 16, 32),
# (7, 11, 13, 17, 33),
# (8, 12, 14, 18, 34),
# (9, 13, 15, 35),
# (10, 14, 36),
# #
# (11, 17, 19, 37),
# (12, 16, 18, 20, 38),
# (13, 17, 21, 39),
# #
# (16, 20, 40),
# (17, 19, 21, 41),
# (18, 20, 42),
# # top layer
# (1, 23, 27),
# (2, 22, 24, 28),
# (3, 23, 25, 29),
# (4, 24, 26, 30),
# (5, 25, 31),
# #
# (6, 22, 28, 32),
# (7, 23, 27, 29, 33),
# (8, 24, 28, 30, 34),
# (9, 25, 29, 31, 35),
# (10, 26, 30, 36),
# #
# (11, 27, 33, 37),
# (12, 28, 32, 34, 38),
# (13, 29, 33, 35, 39),
# (14, 30, 34, 36),
# (15, 31, 35),
# #
# (16, 32, 38, 40),
# (17, 33, 37, 39, 41),
# (18, 34, 38, 42),
# #
# (19, 37, 41),
# (20, 38, 40, 42),
# (21, 39, 41),
# ),
node_hierarchy=(
# hierarchy enum, node number, prescribed (x, y, z)
Hierarchy.PRESCRIBED, # 1 -> (0, 0, 0)
Hierarchy.PRESCRIBED, # 2 -> (1, 0, 0)
Hierarchy.PRESCRIBED, # 3 -> (2, 0, 0)
Hierarchy.PRESCRIBED, # 4 -> (3, 0, 0)
Hierarchy.PRESCRIBED, # 5 -> (4, 0, 0)
Hierarchy.PRESCRIBED, # 6 -> (0, 1, 0)
Hierarchy.BOUNDARY, # 7
Hierarchy.BOUNDARY, # 8
Hierarchy.BOUNDARY, # 9
Hierarchy.PRESCRIBED, # 10 -> (4.5*cos(15 deg), 4.5*sin(15 deg), 0)
Hierarchy.PRESCRIBED, # 11 -> *(0, 2, 0)
Hierarchy.BOUNDARY, # 12
Hierarchy.BOUNDARY, # 13
Hierarchy.BOUNDARY, # 14
Hierarchy.PRESCRIBED, # 15 -> (4.5*cos(30 deg), 4.5*sin(30 deg), 0)
Hierarchy.PRESCRIBED, # 16 -> (0, 3, 0)
Hierarchy.BOUNDARY, # 17
Hierarchy.BOUNDARY, # 18
Hierarchy.PRESCRIBED, # 19 -> (0, 4, 0)
Hierarchy.PRESCRIBED, # 20 -> (1.5, 4, 0)
Hierarchy.PRESCRIBED, # 21 -> (3.5, 4, 0)
#
Hierarchy.PRESCRIBED, # 22 -> (0, 0, 1)
Hierarchy.PRESCRIBED, # 23 -> (1, 0, 1)
Hierarchy.PRESCRIBED, # 24 -> (2, 0, 1)
Hierarchy.PRESCRIBED, # 25 -> (3, 0, 1)
Hierarchy.PRESCRIBED, # 26 -> (4, 0, 1)
Hierarchy.PRESCRIBED, # 27 -> (0, 1, 1)
Hierarchy.BOUNDARY, # 28
Hierarchy.BOUNDARY, # 29
Hierarchy.BOUNDARY, # 30
Hierarchy.PRESCRIBED, # 31 -> (4.5*cos(15 deg), 4.5*sin(15 deg), 1)
Hierarchy.PRESCRIBED, # 32 -> *(0, 2, 1)
Hierarchy.BOUNDARY, # 33
Hierarchy.BOUNDARY, # 34
Hierarchy.BOUNDARY, # 35
Hierarchy.PRESCRIBED, # 36 -> (4.5*cos(30 deg), 4.5*sin(30 deg), 1)
Hierarchy.PRESCRIBED, # 37 -> (0, 3, 1)
Hierarchy.BOUNDARY, # 38
Hierarchy.BOUNDARY, # 39
Hierarchy.PRESCRIBED, # 40 -> (0, 4, 1)
Hierarchy.PRESCRIBED, # 41 -> (1.5, 4, 1)
Hierarchy.PRESCRIBED, # 42 -> (3.5, 4, 1)
),
prescribed_nodes=(
(1, Vertex(0, 0, 0)),
(2, Vertex(1, 0, 0)),
(3, Vertex(2, 0, 0)),
(4, Vertex(3, 0, 0)),
(5, Vertex(4, 0, 0)),
(6, Vertex(0, 1, 0)),
(
10,
Vertex(4.5 * math.cos(15 * DEG2RAD), 4.5 * math.sin(15 * DEG2RAD), 0),
),
(11, Vertex(0, 2, 0)),
(
15,
Vertex(4.5 * math.cos(30 * DEG2RAD), 4.5 * math.sin(30 * DEG2RAD), 0),
),
(16, Vertex(0, 3, 0)),
(19, Vertex(0, 4, 0)),
(20, Vertex(1.5, 4, 0)),
(21, Vertex(3.5, 4, 0)),
(22, Vertex(0, 0, 1)),
(23, Vertex(1, 0, 1)),
(24, Vertex(2, 0, 1)),
(25, Vertex(3, 0, 1)),
(26, Vertex(4, 0, 1)),
(27, Vertex(0, 1, 1)),
(
31,
Vertex(4.5 * math.cos(15 * DEG2RAD), 4.5 * math.sin(15 * DEG2RAD), 1),
),
(32, Vertex(0, 2, 1)),
(
36,
Vertex(4.5 * math.cos(30 * DEG2RAD), 4.5 * math.sin(30 * DEG2RAD), 1),
),
(37, Vertex(0, 3, 1)),
(40, Vertex(0, 4, 1)),
(41, Vertex(1.5, 4, 1)),
(42, Vertex(3.5, 4, 1)),
),
scale_lambda=0.3,
scale_mu=-0.33,
num_iters=10,
algorithm=SmoothingAlgorithm.LAPLACE,
file_stem="bracket",
)
# Double X two-element example
double_x = Example(
vertices=(
Vertex(0.0, 0.0, 0.0),
Vertex(1.0, 0.0, 0.0),
Vertex(2.0, 0.0, 0.0),
Vertex(0.0, 1.0, 0.0),
Vertex(1.0, 1.0, 0.0),
Vertex(2.0, 1.0, 0.0),
Vertex(0.0, 0.0, 1.0),
Vertex(1.0, 0.0, 1.0),
Vertex(2.0, 0.0, 1.0),
Vertex(0.0, 1.0, 1.0),
Vertex(1.0, 1.0, 1.0),
Vertex(2.0, 1.0, 1.0),
),
elements=(
(1, 2, 5, 4, 7, 8, 11, 10),
(2, 3, 6, 5, 8, 9, 12, 11),
),
nelx=2,
nely=1,
nelz=1,
# neighbors=(
# (2, 4, 7),
# (1, 3, 5, 8),
# (2, 6, 9),
# (1, 5, 10),
# (2, 4, 6, 11),
# (3, 5, 12),
# (1, 8, 10),
# (2, 7, 9, 11),
# (3, 8, 12),
# (4, 7, 11),
# (5, 8, 10, 12),
# (6, 9, 11),
# ),
node_hierarchy=(
Hierarchy.BOUNDARY,
Hierarchy.BOUNDARY,
Hierarchy.BOUNDARY,
Hierarchy.BOUNDARY,
Hierarchy.BOUNDARY,
Hierarchy.BOUNDARY,
Hierarchy.BOUNDARY,
Hierarchy.BOUNDARY,
Hierarchy.BOUNDARY,
Hierarchy.BOUNDARY,
Hierarchy.BOUNDARY,
Hierarchy.BOUNDARY,
),
prescribed_nodes=None,
scale_lambda=0.3,
scale_mu=-0.33,
num_iters=2,
algorithm=SmoothingAlgorithm.LAPLACE,
file_stem="double_x",
)
smoothing_figures.py
r"""This module, smoothing_figures.py, illustrates test cases for
smoothing algorithms.
Example
-------
source ~/autotwin/automesh/.venv/bin/activate
cd ~/autotwin/automesh/book/smoothing
python smoothing_figures.py
"""
import datetime
from pathlib import Path
from typing import Final
from matplotlib.colors import LightSource
import matplotlib.pyplot as plt
import numpy as np
import smoothing as sm
import smoothing_examples as se
import smoothing_types as ty
# Type alias for functional style methods
# https://docs.python.org/3/library/typing.html#type-aliases
# DofSet = ty.DofSet
Hexes = ty.Hexes
Neighbors = ty.Neighbors
NodeHierarchy = ty.NodeHierarchy
Vertex = ty.Vertex
Vertices = ty.Vertices
SmoothingAlgorithm = ty.SmoothingAlgorithm
# Examples
# ex = se.double_x
ex = se.bracket # overwrite
# Visualization
width, height = 10, 5
# width, height = 8, 4
# width, height = 6, 3
fig = plt.figure(figsize=(width, height))
# fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(1, 2, 1, projection="3d") # r1, c2, 1st subplot
ax2 = fig.add_subplot(1, 2, 2, projection="3d") # r1, c2, 2nd subplot
el, az, roll = 63, -110, 0
cmap = plt.get_cmap(name="tab10")
# NUM_COLORS = len(spheres)
NUM_COLORS = 10
VOXEL_ALPHA: Final[float] = 0.9
LINE_ALPHA: Final[float] = 0.5
colors = cmap(np.linspace(0, 1, NUM_COLORS))
lightsource = LightSource(azdeg=325, altdeg=45) # azimuth, elevation
# lightsource = LightSource(azdeg=325, altdeg=90) # azimuth, elevation
# OUTPUT_DIR: Final[Path] = Path(__file__).parent
DPI: Final[int] = 300 # resolution, dots per inch
SHOW: Final[bool] = True # Shows the figure on screen
SAVE: Final[bool] = True # Saves the .png and .npy files
# output_png_short = ex.file_stem + ".png"
# output_png: Path = (
# Path(output_dir).expanduser().joinpath(output_png_short)
# )
nx, ny, nz = ex.nelx, ex.nely, ex.nelz
nzp, nyp, nxp = nz + 1, ny + 1, nx + 1
# breakpoint()
vertices_laplace = sm.smooth(
vv=ex.vertices,
hexes=ex.elements,
node_hierarchy=ex.node_hierarchy,
prescribed_nodes=ex.prescribed_nodes,
scale_lambda=ex.scale_lambda,
num_iters=ex.num_iters,
algorithm=ex.algorithm,
)
# original vertices
xs = [v.x for v in ex.vertices]
ys = [v.y for v in ex.vertices]
zs = [v.z for v in ex.vertices]
# laplace smoothed vertices
xs_l = [v.x for v in vertices_laplace]
ys_l = [v.y for v in vertices_laplace]
zs_l = [v.z for v in vertices_laplace]
# breakpoint()
# draw edge lines
ep = sm.edge_pairs(ex.elements) # edge pairs
line_segments = [
(sm.xyz(ex.vertices[p1 - 1]), sm.xyz(ex.vertices[p2 - 1])) for (p1, p2) in ep
]
line_segments_laplace = [
(sm.xyz(vertices_laplace[p1 - 1]), sm.xyz(vertices_laplace[p2 - 1]))
for (p1, p2) in ep
]
for ls in line_segments:
x0x1 = [pt[0] for pt in ls]
y0y1 = [pt[1] for pt in ls]
z0z1 = [pt[2] for pt in ls]
ax.plot3D(
x0x1,
y0y1,
z0z1,
linestyle="solid",
linewidth=0.5,
color="blue",
)
# draw nodes
ax.scatter(
xs,
ys,
zs,
s=20,
facecolors="blue",
edgecolors="none",
)
# repeat with lighter color on second axis
for ls in line_segments:
x0x1 = [pt[0] for pt in ls]
y0y1 = [pt[1] for pt in ls]
z0z1 = [pt[2] for pt in ls]
ax2.plot3D(
x0x1,
y0y1,
z0z1,
linestyle="dashed",
linewidth=0.5,
color="blue",
alpha=LINE_ALPHA,
)
for ls in line_segments_laplace:
x0x1 = [pt[0] for pt in ls]
y0y1 = [pt[1] for pt in ls]
z0z1 = [pt[2] for pt in ls]
ax2.plot3D(
x0x1,
y0y1,
z0z1,
linestyle="solid",
linewidth=0.5,
color="red",
)
ax2.scatter(
xs,
ys,
zs,
s=20,
facecolors="blue",
edgecolors="none",
alpha=0.5,
)
ax2.scatter(
xs_l,
ys_l,
zs_l,
s=20,
facecolors="red",
edgecolors="none",
)
# Set labels for the axes
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("z")
# repeat for the 2nd axis
ax2.set_xlabel("x")
ax2.set_ylabel("y")
ax2.set_zlabel("z")
x_ticks = list(range(nxp))
y_ticks = list(range(nyp))
z_ticks = list(range(nzp))
ax.set_xticks(x_ticks)
ax.set_yticks(y_ticks)
ax.set_zticks(z_ticks)
# repeat for the 2nd axis
ax2.set_xticks(x_ticks)
ax2.set_yticks(y_ticks)
ax2.set_zticks(z_ticks)
ax.set_xlim(float(x_ticks[0]), float(x_ticks[-1]))
ax.set_ylim(float(y_ticks[0]), float(y_ticks[-1]))
ax.set_zlim(float(z_ticks[0]), float(z_ticks[-1]))
# repeat for the 2nd axis
ax2.set_xlim(float(x_ticks[0]), float(x_ticks[-1]))
ax2.set_ylim(float(y_ticks[0]), float(y_ticks[-1]))
ax2.set_zlim(float(z_ticks[0]), float(z_ticks[-1]))
# Set the camera view
ax.set_aspect("equal")
ax.view_init(elev=el, azim=az, roll=roll)
# # Set the projection to orthographic
# # ax.view_init(elev=0, azim=-90) # Adjust the view angle if needed
# repeat for the 2nd axis
ax2.set_aspect("equal")
ax2.view_init(elev=el, azim=az, roll=roll)
# File name
aa = Path(__file__)
fig_path = Path(__file__).parent
# fig_stem = Path(__file__).stem
fig_stem = ex.file_stem
# breakpoint()
FIG_EXT: Final[str] = ".png"
bb = fig_path.joinpath(fig_stem + "_iter_" + str(ex.num_iters) + FIG_EXT)
# Add a footnote
# Get the current date and time in UTC
now_utc = datetime.datetime.now(datetime.UTC)
# Format the date and time as a string
timestamp_utc = now_utc.strftime("%Y-%m-%d %H:%M:%S UTC")
fn = f"Figure: {bb.name} "
fn += f"created with {__file__}\non {timestamp_utc}."
fig.text(0.5, 0.01, fn, ha="center", fontsize=8)
# fig.tight_layout() # don't use as it clips the x-axis label
if SHOW:
plt.show()
if SAVE:
fig.savefig(bb, dpi=DPI)
print(f"Saved: {bb}")
print("End of script.")
Isosurface
Isosurfacing is a method to extract the surface from a three-dimensional scalar field. A scalar field , is a function that assigns a scalar value to every point in three-dimensional space. For the special case when all points in the domain are aligned into a regular (i.e., uniform) three-dimensional grid, the scalar field composes a voxel field.
The simplest example of non-trivial voxel field consists of a range of only two integer values, for example,
0 and 1, where 0 indicates a point in the grid is outside the field, and where 1 indicates a
point in the grid is inside (or on the boundary of) the field. The interface between 0 and 1 everywhere in the grid composes the isosurface of the field.
Given a voxel field, the isosurface can estimated with two common techniques: Marching Cubes (MC) and Dual Contouring (DC). Lorensen and Cline1 originally proposed MC in 1987. DC was originally proposed by Ju et al.2 in 2002.
Marching Cubes
MC operates on each voxel in the 3D grid on a independent basis.
For each voxel, the eight nodes of the voxel are evaluated as outside (0) the scalar field or inside (1) the scalar field. The eight nodes, classified as either 0 or 1, create 256 () possible configurations. Of these combinations, only 15 are unique configurations, after symmmetry and rotation considerations. For each configuration, MC generates a set of triangles to approximate the isosurface.
Advantages
- Simple implementation; uses only interpolation between voxel corners.
- Results in smooth surfaces because it interpolates along edges between voxel corners. This can be an advantage when smooth meshes are desired but is a disadvantage when sharp edges are desired.
Disadvantages
- Can produce ambiguous cases wherein the isosurface can be represented in multiple (non-unique) ways. This can result in a surface artifacts.
- Can produce non-manifold edges.
Manifold: "The mesh forms a 2D manifold if the local topology is everywhere equivalent to a disc; that is, if the neighborhood of every feature consists of a connected ring of polygons forming a single surface (see Figure 2 of Luebke3 reproduced below). In a triangulated mesh displaying manifold topology, exactly two triangles share every edge, and every triangle shares an edge with exactly three neighboring triangles. A 2D manifold with boundary permits boundary edges, which belong to only one triangle."
| maniford | non-manifold |
|---|---|
 |  |
Figure: Reproduction of Luebke3 Figure 2 (left) showing a manifold mesh, and Figure 3 (right) showing a non-manifold mesh because of (a) an edge shared by more than two triangles, (b) a vertex shared by two unconnected sets of triangles, and (c) a T-junction vertex.
Dual Contouring
DC improves upon the MC algorithm. DC uses the dual grid of the voxel data, locating nodes of the surface within the voxel, rather than on the edge of the voxel (as done with MC).
Boris4 created a figure, reproduced below, that illustrates the differences between MC and DC.
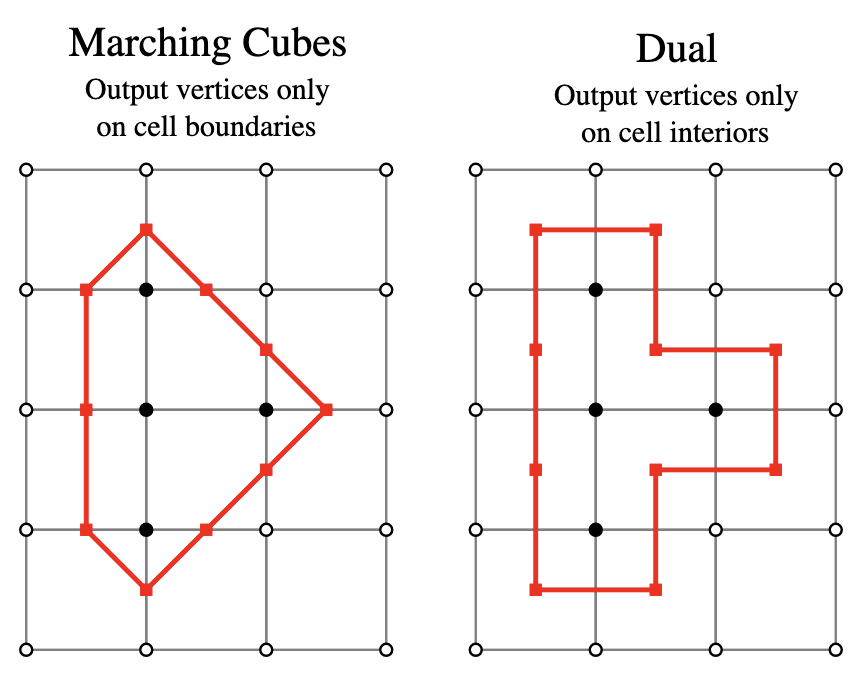
Figure: Reproduction of the figure from Boris4, illustrating, in two dimentions, the differences between MC and DC. White circle are outside points. Black circles are inside points. In MC, the red points indicate surface vertices at edge intersections. In DC, the red points indicate surface vertices within a voxel.
Advantages
- "[C]an produce sharp features by inserting vertices anywhere inside the grid cube, as opposed to the Marching Cubes (MC) algorithm that can insert vertices only on grid edges."5
Disadvantages
- More complicated than MC since DC uses both position and normal (gradient) information at voxel edges to locate the surface intersection.
- "...unable to guarantee 2-manifold and watertight meshes due to the fact that it produces only one vertex for each grid cube." "DC is that it does not guarantee 2-manifold and intersection-free surfaces. A polygonal mesh is considered as being 2-manifold if each edge of the mesh is shared by only two faces, and if the neighborhood of each vertex of the mesh is the topological equivalent of a disk." 5
References
-
Lorensen WF. Marching cubes: A high resolution 3D surface construction algorithm. Computer Graphics. 1987;21. link ↩
-
Ju T, Losasso F, Schaefer S, Warren J. Dual contouring of hermite data. In Proceedings of the 29th annual conference on Computer graphics and interactive techniques 2002 Jul 1 (pp. 339-346). link ↩
-
Luebke DP. A developer's survey of polygonal simplification algorithms. IEEE Computer Graphics and Applications. 2001 May;21(3):24-35. link ↩ ↩2
-
Boris. Dual Contouring Tutorial. Available from: https://www.boristhebrave.com/2018/04/15/dual-contouring-tutorial/ [Accessed 18 Jan 2025]. link ↩ ↩2
-
Rashid T, Sultana S, Audette MA. Watertight and 2-manifold surface meshes using dual contouring with tetrahedral decomposition of grid cubes. Procedia engineering. 2016 Jan 1;163:136-48. link ↩ ↩2
Subdivision
Surface subdivision is a geometric modeling technique that defines smooth curves or surfaces as the limit of a sequence of successive refinements.
Developed as a generalization of spline surfaces, subdivision allows for the representation of complex, arbitrary control meshes while avoiding the topological constraints and "cracking" issues often associated with traditional Non-Uniform Rational B-Splines (NURBS).
Various algorithms have been established to handle different mesh types and desired continuity:
- The Catmull-Clark scheme is frequently used for quadrilateral meshes to produce continuous surfaces, while
- The Loop subdivision scheme is a popular approximating method specifically designed for triangular meshes.
By iteratively applying simple refinement rules—typically involving a "splitting" step to increase resolution and an "averaging" step to relocate vertices—subdivision transforms a coarse initial shape into a highly detailed, smooth limit surface suitable for high-end animation and scalable rendering.
Octa Loop
This example uses Loop subdivision to transform an octahedron into a sphere. The results below are based on Octa-Loop Subdivision Scheme (GitHub).
We create a unit radius octahedron template, and successively refine it into a sphere. The sphere is a useful baseline subject of study because it:
- Can easily be approximated by a voxel stack at various resolutions,
- Can easily be approximated by a finite element mesh,
- Has a known analytic volume, and
- Has a known analytic local curvature.
Base Octahedron
We created a unit radius template, octa_base.obj, with contents listed below:
v 1.0 0.0 0.0
v 0.0 1.0 0.0
v -1.0 0.0 0.0
v 0.0 -1.0 0.0
v 0.0 0.0 1.0
v 0.0 0.0 -1.0
f 1 2 5
f 2 3 5
f 3 4 5
f 4 1 5
f 2 1 6
f 3 2 6
f 4 3 6
f 1 4 6
Refinement
The refinement below was created with MeshLab 2022.02, Subdivision Surfaces LS3 Loop, based on Boye et al.1
| name | image | file size |
|---|---|---|
octa_loop0.stl |  | 2.1kB |
octa_loop1.stl |  | 8.3kB |
octa_loop2.stl |  | 33kB |
octa_loop3.stl |  | 132kB |
octa_loop4.stl |  | 526kB |
octa_loop5.stl G |  | 2.1MB |
octa_loop6.stl G | 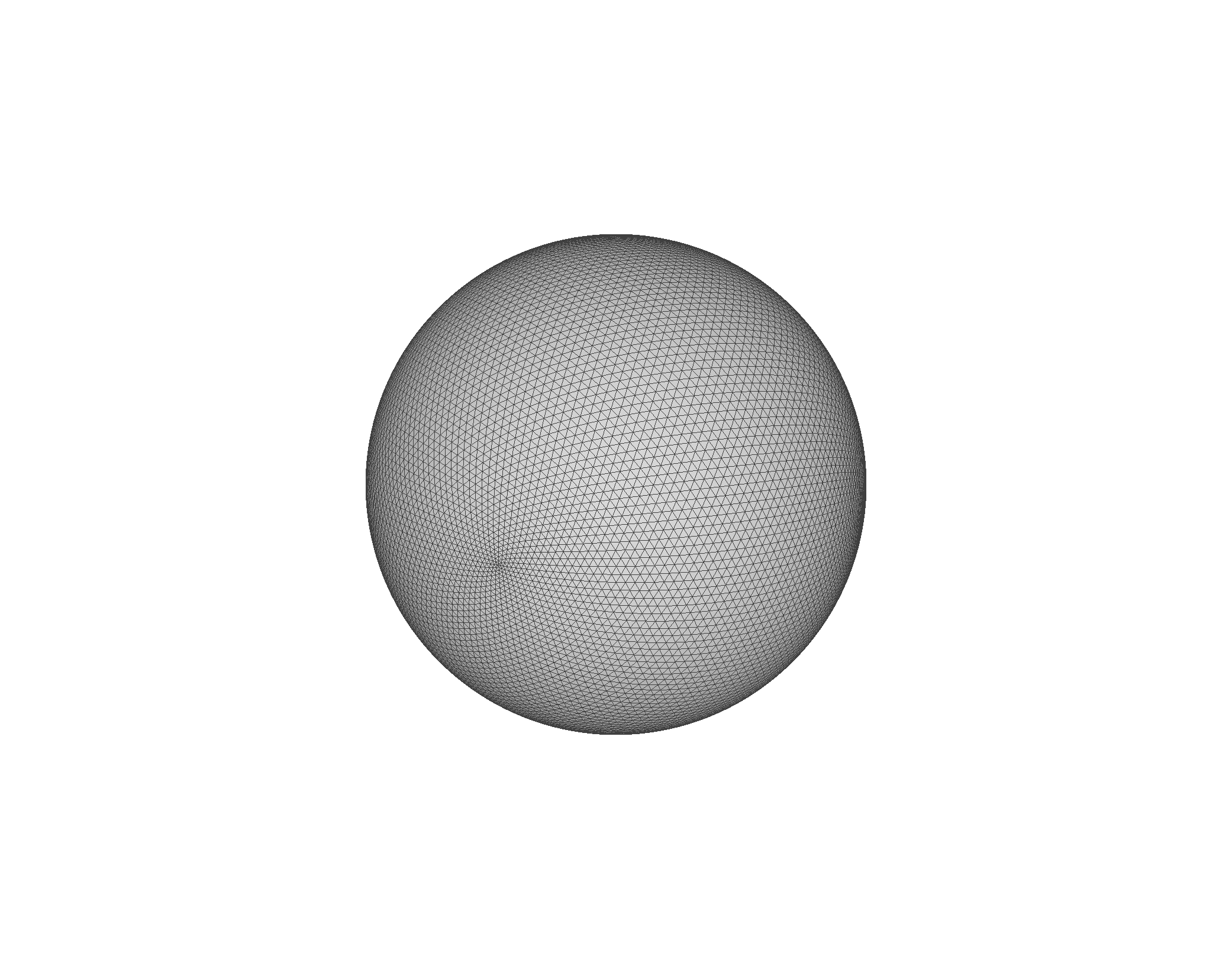 | 8.6MB |
octa_loop7.stl G |  | 33MB |
Items with
Gare not on the repository; they are on Google Drive because of their large file size.
Geometric Metrics
- The surface area of a sphere is , and when , .
- The volume of a sphere is , and when , .
Using the Euler Characteristic for a sphere (), we can verify the progression from the base octahedron ():
| Iteration () | Vertices () | Edges () | Faces () | Calculation () |
|---|---|---|---|---|
| 0 (Base) | 6 | 12 | 8 | 6+12=18 |
| 1 | 18 | 48 | 32 | 18+48=66 |
| 2 | 66 | 192 | 128 | 66+192=258 |
| 3 | 258 | 768 | 512 | 258+768=1,026 |
| 4 | 1,026 | 3,072 | 2,048 | 1,026+3,072=4,098 |
| 5 | 4,098 | 12,288 | 8,192 | 4,098+12,288=16,386 |
| 6 | 16,386 | 49,152 | 32,768 | 16,386+49,152=65,538 |
| 7 | 65,538 | 196,608 | 131,072 | 65,538+196,608=262,146 |
The recursive relationships for a closed triangular mesh:
- Faces:
- Edges:
- Vertices:
Sculpt Baseline
We created Sculpt baseline meshes with the sculpt_stl_to_inp.py script as
(atmeshenv) ~/autotwin/mesh/src/atmesh> python sculpt_stl_to_inp.py
and create standard views in Cubit with
Cubit>
graphics perspective off # orthogonal, not perspective view
up 0 0 1 # z-axis points up
view iso # isometric x, y, z camera
quality volume 1 scaled jacobian global draw histogram draw mesh list
to produce the following results:
| iter | image | cells | nodes nnp | elements nel | element density nel |
|---|---|---|---|---|---|
| 0 |  | 35x35x35 | 8,696 | 7,343 | 5,507 |
| 1 |  | 28x28x28 | 8,133 | 6,960 | 2,365 |
| 2 | 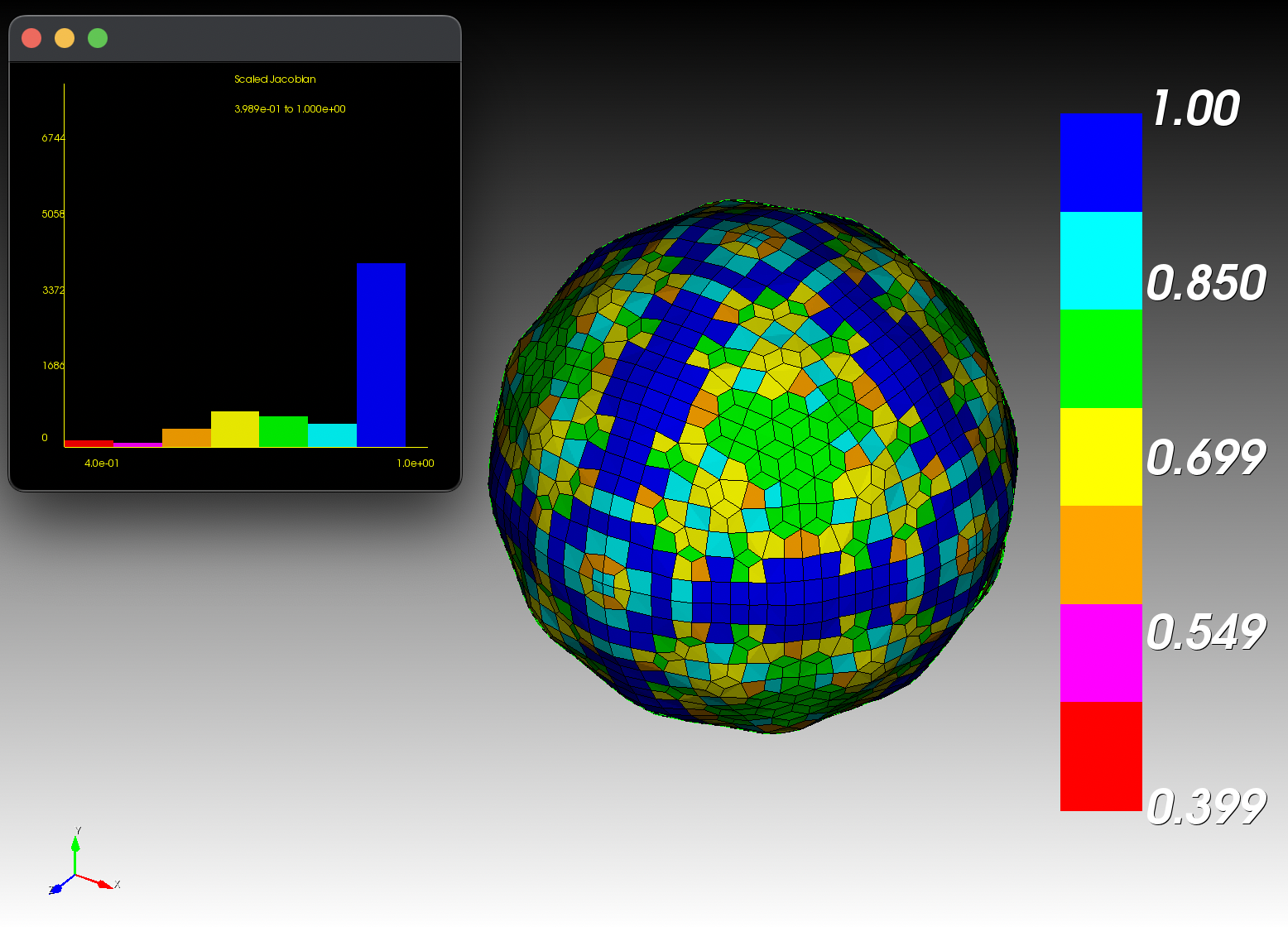 | 26x26x26 | 7,833 | 6,744 | 1,762 |
| 3 | 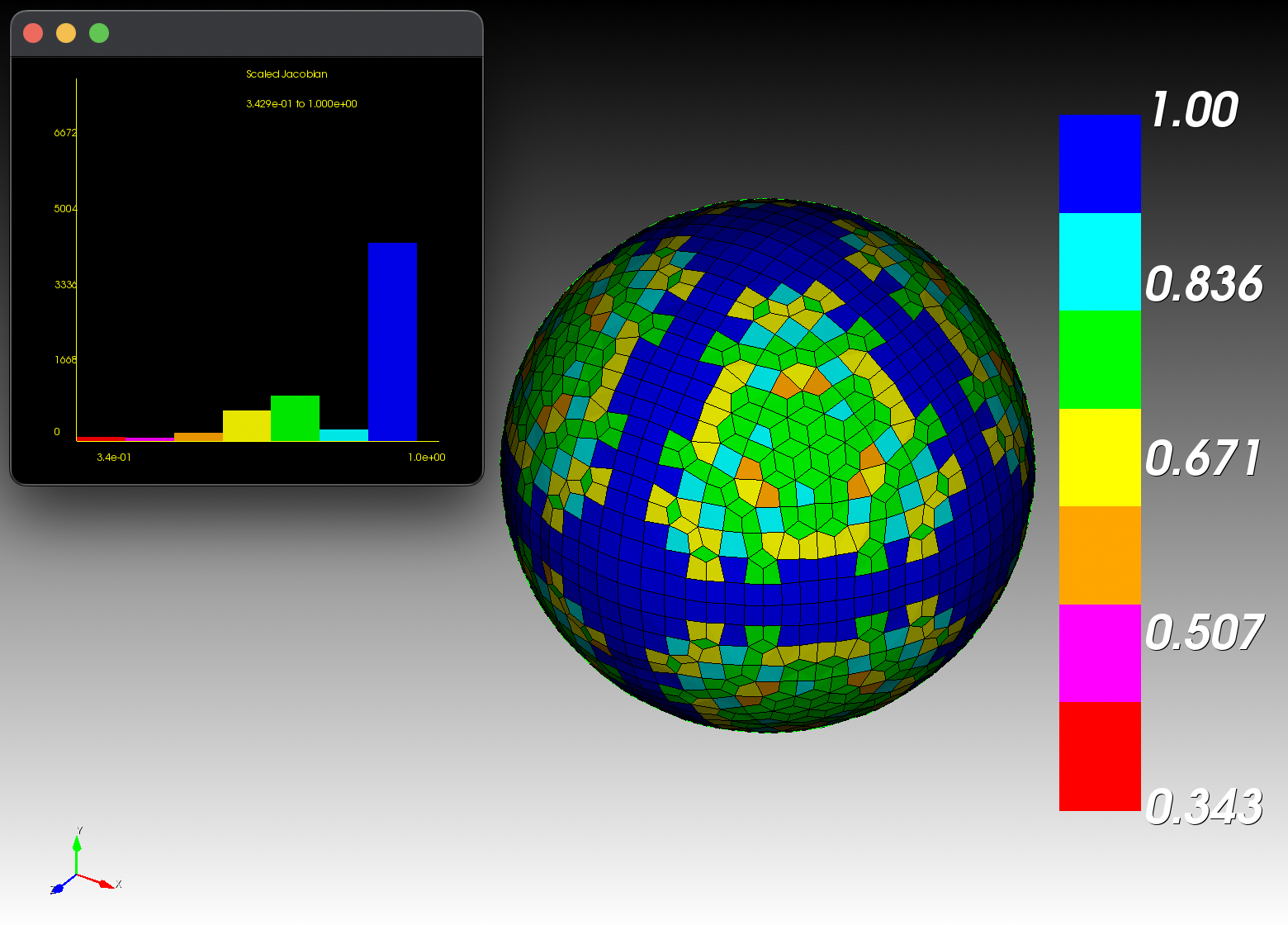 | 26x26x26 | 7,731 | 6,672 | 1,630 |
| 4 | 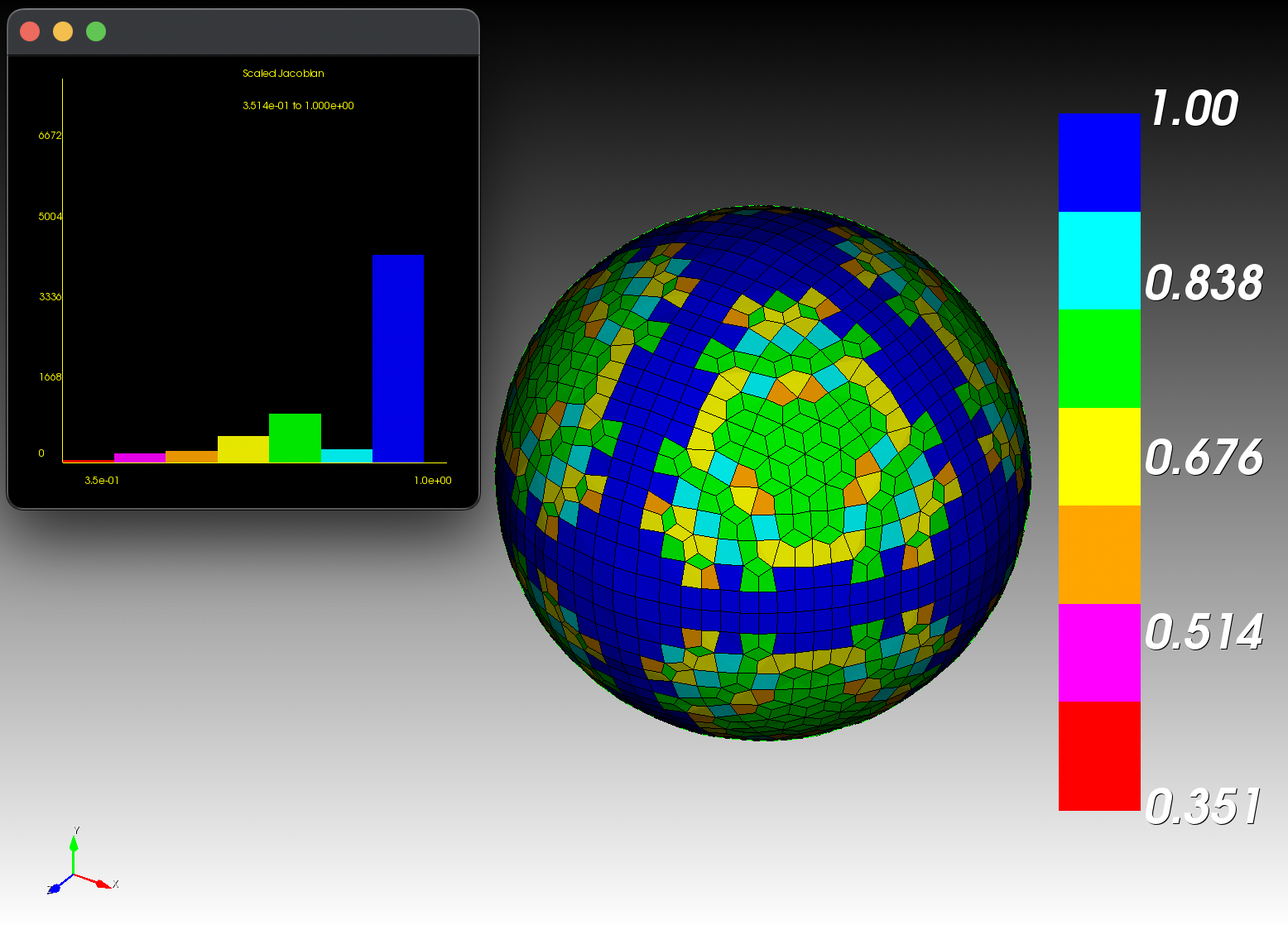 | 26x26x26 | 7,731 | 6,672 | 1,600 |
| 5 | 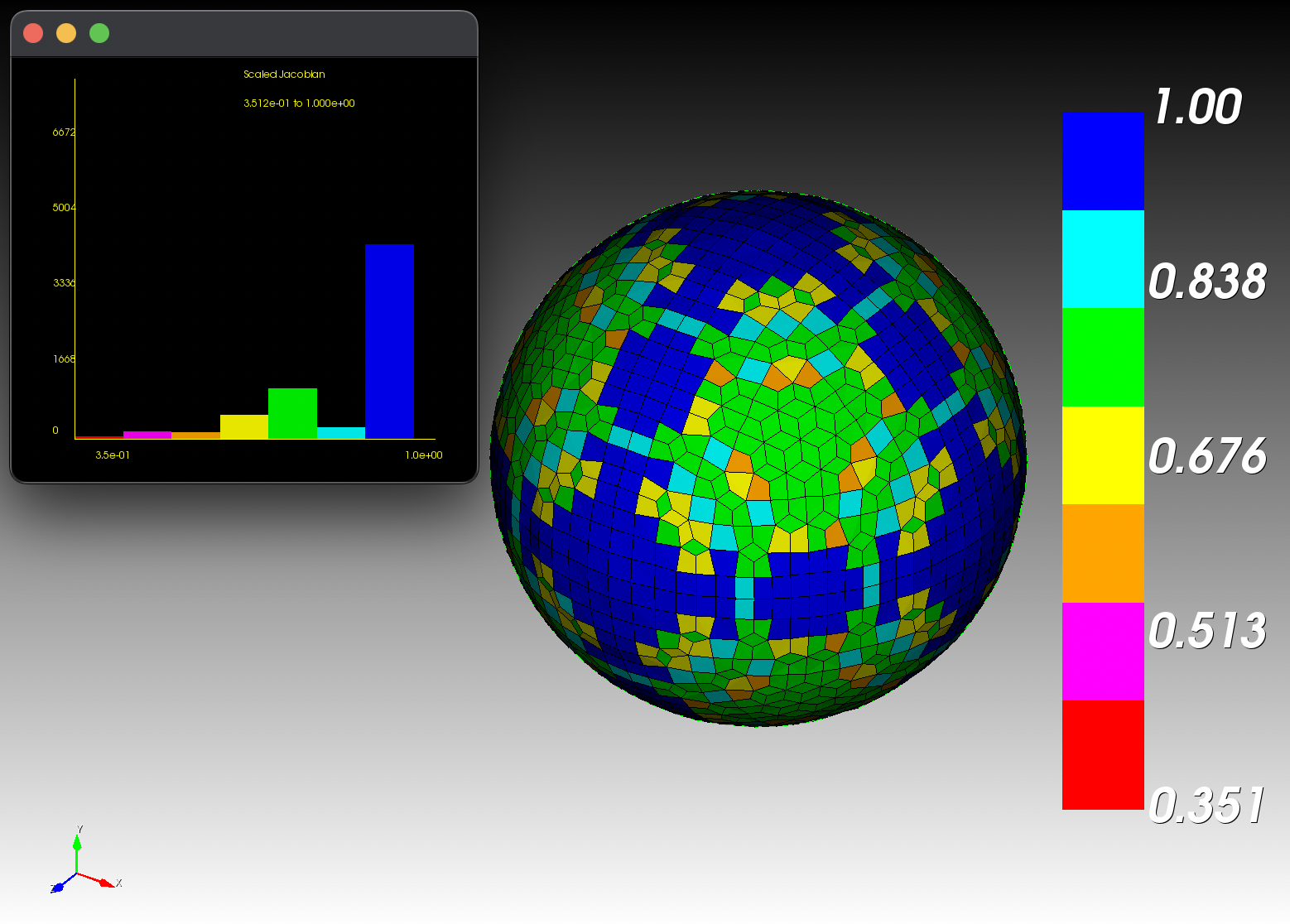 | 26x26x26 | 7,731 | 6,672 | 1,596 |
| 6 | 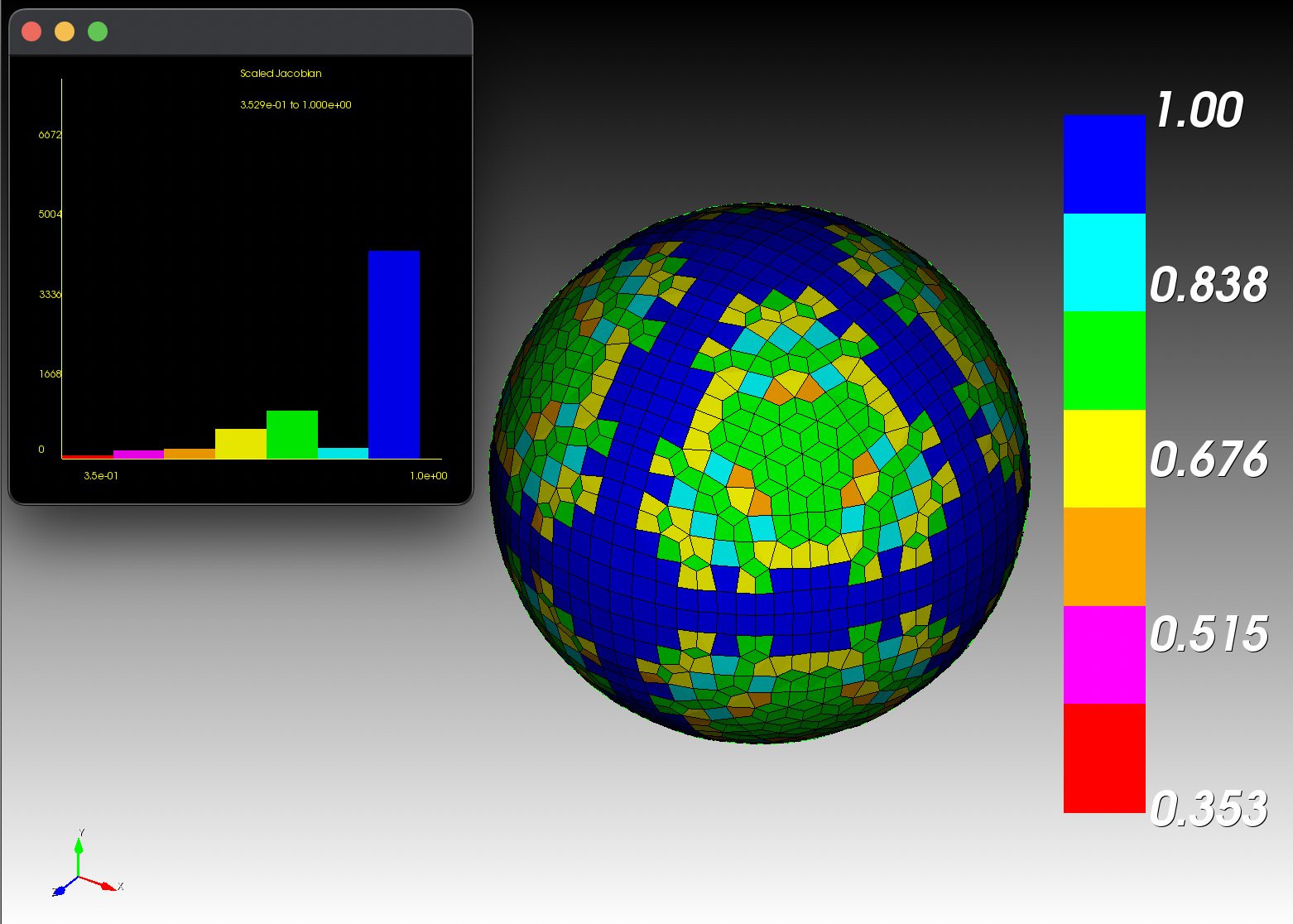 | 26x26x26 | 7,731 | 6,672 | 1,595 |
| 7 | 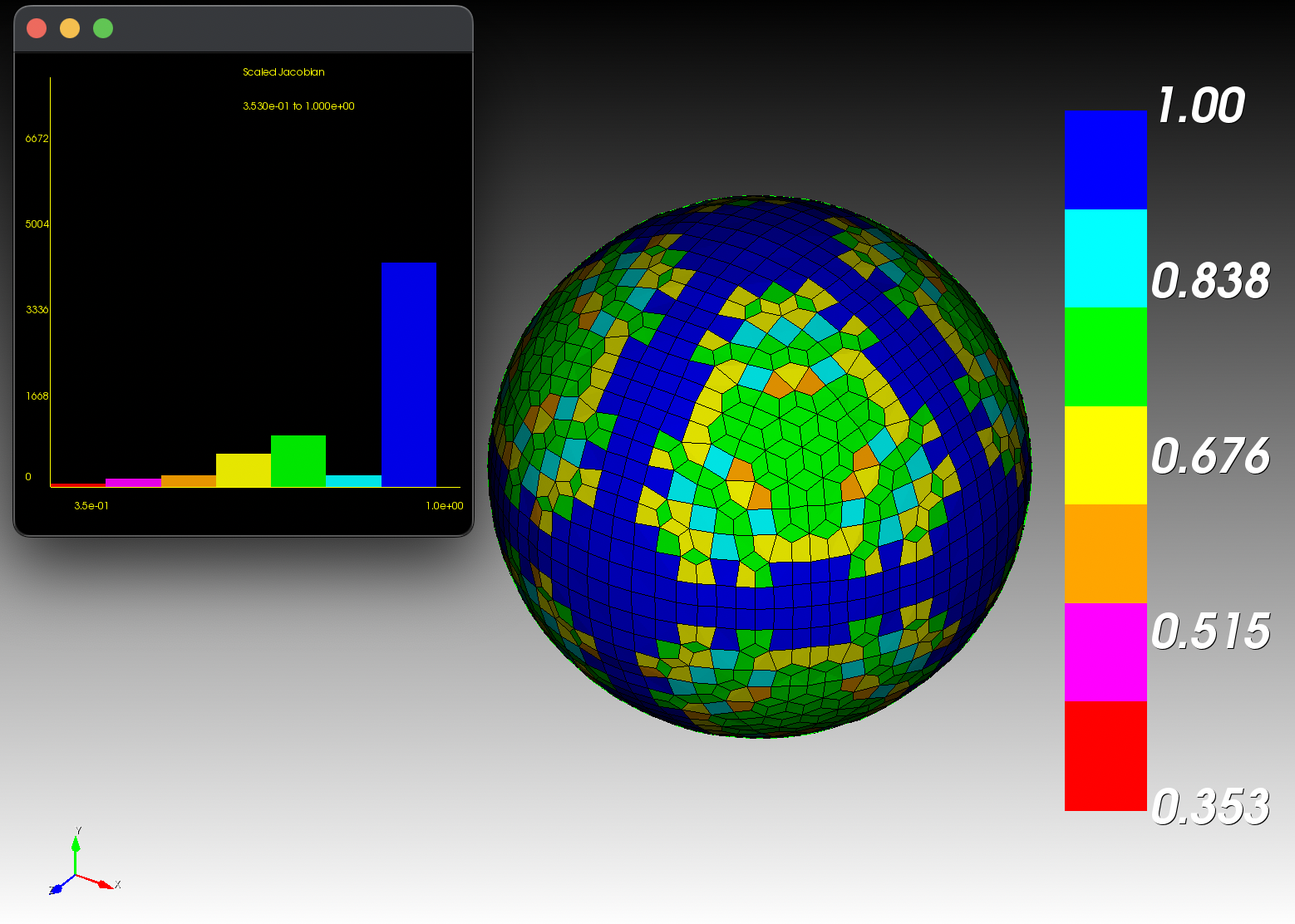 | 26x26x26 | 7,731 | 6,672 | 1,595 |
References
- Octa-Loop Subdivision Scheme (GitHub)
- Documentation detailing the Octa-Loop scheme, a variant of Loop subdivision optimized for octahedrally refined meshes.
- Subdivision Surfaces Lecture Notes (Stanford University)
- A comprehensive academic overview of subdivision concepts, including the mathematical foundations of the Catmull-Clark and Loop schemes.
- Stanford cs468-10-fall Subdivision http://graphics.stanford.edu/courses/cs468-10-fall/LectureSlides/10_Subdivision.pdf and Google Drive repo copy
- Catmull–Clark Subdivision Surface (Rosetta Code)
- A technical resource providing algorithmic steps and multi-language code implementations for the Catmull-Clark subdivision process.
- Recursively Generated B-Spline Surfaces (Original Paper)
- The seminal 1978 paper by Edwin Catmull and James Clark that introduced the method for generating smooth surfaces from arbitrary topological meshes (referenced within the other materials).
- Catmull, E., & Clark, J. (1978). Recursively generated B-spline surfaces on arbitrary topological meshes. Computer-Aided Design, 10(6), 350-355. https://doi.org/10.1016/0010-4485(78)90110-0
- Loop, C. (1987). Smooth subdivision surfaces based on triangles [Master's thesis, University of Utah]. https://www.microsoft.com/en-us/research/wp-content/uploads/2016/02/thesis-1.pdf
- https://docs.juliahub.com/Meshes/FuRcu/0.17.1/algorithms/refinement.html#Catmull-Clark
-
Boyé S, Guennebaud G, Schlick C. Least squares subdivision surfaces. In Computer Graphics Forum 2010 Sep (Vol. 29, No. 7, pp. 2021-2028). Oxford, UK: Blackwell Publishing Ltd. ↩
Dualization
Dualization is the process of using a primal mesh to construct a dual mesh. Dualization can be performed on 2D/3D surface meshes composed of quadrilateral elements, and 3D volumetric meshes composed of hexahedral elements. Both quadrilateral and hexahedral elements will be discussed.
Quadtree
With plot_quadtree_convention.py, we create the following index scheme:
With fig_quadtree.tex, we create the following image of the inverted tree:
With plot_quadtree.py, we plot a domain
- A square domain
L0 - Single point at
(2.6, 0.6)to trigger refinement.
| Level 0 | 1 | 2 |
|---|---|---|
 |  |  |
| 3 | 4 | 5 |
|---|---|---|
 | 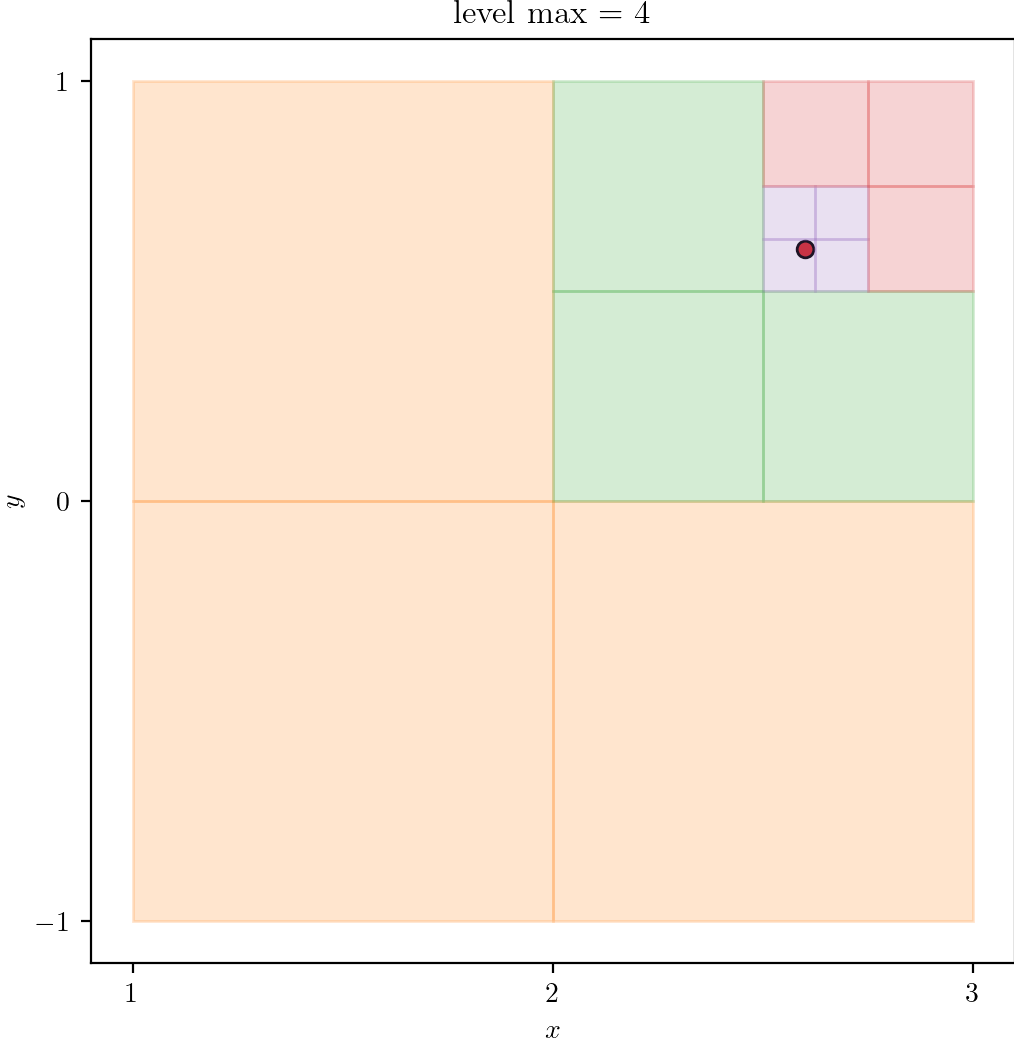 | 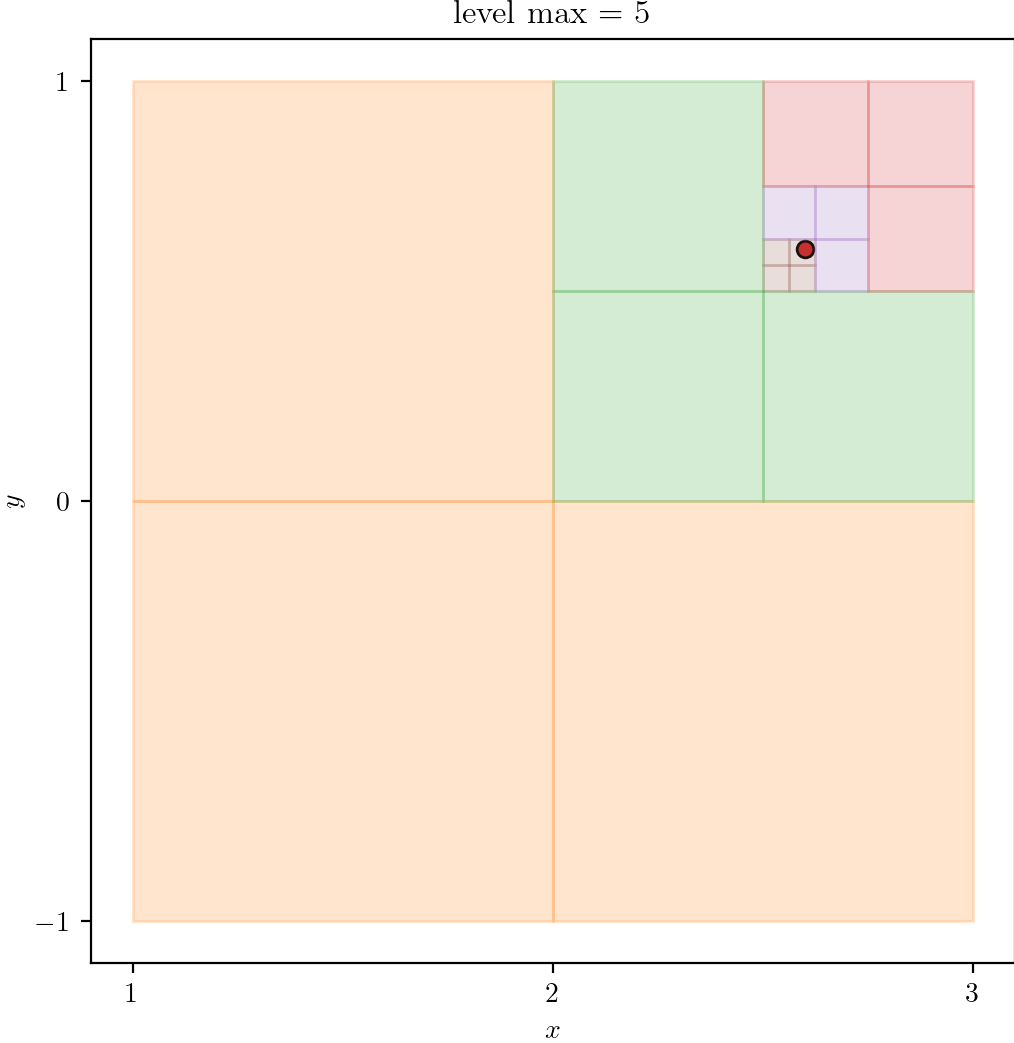 |
Circle from Segmentation
We illustrate the segmentation start point as it applies to quadtree formation.
- For a segmentation at a given resolution of pixels, we immerse the segmentation into a single-cell (
L0) quadtree domain. - We pad the segmentation margins with void (segmentation ID
0) such that the pixel count in all directions ( and )- is the same, and
- is divisible by 2 for cell subdivisions.
- For each cell in the quadtree, we process the cells recursively and ask this question: Does the cell contain more than one material? If yes, then subdivide; if no, then do not subdivide.
| 3 | 4 | 5 | 6 |
|---|---|---|---|
| 13 | 14 | 15 | 16 |
|---|---|---|---|
Circle from Boundary
We illustrate the boundary start point as it applies to quadtree formation.
- We define a boundary as directed series of connected, discrete points that create a closed-loop, non-intersecting path.
- We immerse the boundary into a single-cell (
L0) quadtree domain. - For each cell in the quadtree, we process the cells recursively and ask this question: Does the cell contain at least one boundary point? If yes, then subdivide; if no, then do not subdivide.
Consider a boundary of a circle defined by discrete (x, y) points.
| Level 0 | 1 | 2 |
|---|---|---|
| 3 | 4 | 5 |
|---|---|---|
Circle from Tesellation
We illustrate the tesellation as it applies to quadtree formation.
- We immerse the tesellation into a single-cell (
L0) quadtree domain. - We create a boundary of the tesellation with points that lie on the boundary of the tesellation.
- We immerse the boundary into a single-cell (
L0) quadtree domain. - For each cell in the quadtree, we process the cells recursively and ask this question: Does the cell contain at least one boundary point? If yes, then subdivide; if no, then do not subdivide.
Quarter Plate
With Python, we produce a Quadtree with zero to five levels of refinement. Refinement is triggered based on whether or not a cell contains one or more seed points, shown as points along the quarter circle centered at (4, 0).
| Level 0 | 1 | 2 |
|---|---|---|
| 3 | 4 | 5 |
|---|---|---|
Octree
Sphere
Consider a boundary of a sphere defined by a discrete triangular tesselation.
References
- https://github.com/sandialabs/sibl/blob/master/geo/doc/quadtree.md
- https://github.com/sandialabs/sibl/blob/master/geo/doc/dual_quad_transitions.md
- https://github.com/sandialabs/sibl/blob/master/geo/doc/dual/lesson_11.md
Source
quadtree_plot.py
Command Line Interface
automesh --help
@@@@@@@@@@@@@@@@
@@@@ @@@@@@@@@@
@@@@ @@@@@@@@@@@ automesh: Automatic mesh generation
@@@@ @@@@@@@@@@@@
@@ @@ @@ v0.3.8 linux x86_64
@@ @@ @@ build d01ddd6 2026-02-27T16:44:12+0000
@@@@@@@@@@@@ @@@ Chad B. Hovey <chovey@sandia.gov>
@@@@@@@@@@@ @@@@ Michael R. Buche <mrbuche@sandia.gov>
@@@@@@@@@@ @@@@@ @
@@@@@@@@@@@@@@@@
Usage: automesh [COMMAND]
Commands:
convert Converts between mesh or segmentation file types
defeature Defeatures and creates a new segmentation
diff Show the difference between two segmentations
extract Extracts a specified range of voxels from a segmentation
mesh Creates a finite element mesh from a tessellation or segmentation
metrics Quality metrics for an existing finite element mesh
remesh Applies isotropic remeshing to an existing mesh
segment Creates a segmentation or voxelized mesh from an existing mesh
smooth Applies smoothing to an existing mesh
help Print this message or the help of the given subcommand(s)
Options:
-h, --help Print help
-V, --version Print version
Convert
automesh convert --help
Converts between mesh or segmentation file types
Usage: automesh convert <COMMAND>
Commands:
mesh Converts mesh file types (exo | inp | stl) -> (exo | mesh | stl | vtk)
segmentation Converts segmentation file types (npy | spn) -> (npy | spn)
help Print this message or the help of the given subcommand(s)
Options:
-h, --help Print help
Convert Mesh
automesh convert mesh --help
Converts mesh file types (exo | inp | stl) -> (exo | mesh | stl | vtk)
Usage: automesh convert mesh <COMMAND>
Commands:
hex Converts an all-hexahedral mesh
tet Converts an all-tetrahedral mesh
tri Converts an all-triangular mesh
help Print this message or the help of the given subcommand(s)
Options:
-h, --help Print help
Convert Mesh Hex
automesh convert mesh hex --help
Converts an all-hexahedral mesh
Usage: automesh convert mesh hex [OPTIONS] --input <FILE> --output <FILE>
Options:
-i, --input <FILE> Mesh input file (exo | inp | stl)
-o, --output <FILE> Mesh output file (exo | mesh | stl | vtk)
-q, --quiet Pass to quiet the terminal output
-h, --help Print help
Convert Mesh Tet
automesh convert mesh tet --help
Converts an all-tetrahedral mesh
Usage: automesh convert mesh tet [OPTIONS] --input <FILE> --output <FILE>
Options:
-i, --input <FILE> Mesh input file (exo | inp | stl)
-o, --output <FILE> Mesh output file (exo | mesh | stl | vtk)
-q, --quiet Pass to quiet the terminal output
-h, --help Print help
Convert Mesh Tri
automesh convert mesh tri --help
Converts an all-triangular mesh
Usage: automesh convert mesh tri [OPTIONS] --input <FILE> --output <FILE>
Options:
-i, --input <FILE> Mesh input file (exo | inp | stl)
-o, --output <FILE> Mesh output file (exo | mesh | stl | vtk)
-q, --quiet Pass to quiet the terminal output
-h, --help Print help
Convert Segmentation
automesh convert segmentation --help
Converts segmentation file types (npy | spn) -> (npy | spn)
Usage: automesh convert segmentation [OPTIONS] --input <FILE> --output <FILE>
Options:
-i, --input <FILE> Segmentation input file (npy | spn)
-o, --output <FILE> Segmentation output file (npy | spn)
-x, --nelx <NEL> Number of voxels in the x-direction (spn)
-y, --nely <NEL> Number of voxels in the y-direction (spn)
-z, --nelz <NEL> Number of voxels in the z-direction (spn)
-q, --quiet Pass to quiet the terminal output
-h, --help Print help
Defeature
automesh defeature --help
Defeatures and creates a new segmentation
Usage: automesh defeature [OPTIONS] --input <FILE> --output <FILE> --min <MIN>
Options:
-i, --input <FILE> Segmentation input file (npy | spn)
-o, --output <FILE> Defeatured segmentation output file (npy | spn)
-m, --min <MIN> Defeature clusters with less than MIN voxels
-x, --nelx <NEL> Number of voxels in the x-direction (spn)
-y, --nely <NEL> Number of voxels in the y-direction (spn)
-z, --nelz <NEL> Number of voxels in the z-direction (spn)
-q, --quiet Pass to quiet the terminal output
-h, --help Print help
Diff
automesh diff --help
Show the difference between two segmentations
Usage: automesh diff [OPTIONS] --output <FILE>
Options:
-i, --input <FILE> <FILE> Segmentation input files (npy | spn)
-o, --output <FILE> Segmentation difference output file (npy | spn)
-x, --nelx <NEL> Number of voxels in the x-direction (spn)
-y, --nely <NEL> Number of voxels in the y-direction (spn)
-z, --nelz <NEL> Number of voxels in the z-direction (spn)
-q, --quiet Pass to quiet the terminal output
-h, --help Print help
Extract
automesh extract --help
Extracts a specified range of voxels from a segmentation
Usage: automesh extract [OPTIONS] --input <FILE> --output <FILE> --xmin <MIN> --xmax <MAX> --ymin <MIN> --ymax <MAX> --zmin <MIN> --zmax <MAX>
Options:
-i, --input <FILE> Segmentation input file (npy | spn)
-o, --output <FILE> Extracted segmentation output file (npy | spn)
-x, --nelx <NEL> Number of voxels in the x-direction (spn)
-y, --nely <NEL> Number of voxels in the y-direction (spn)
-z, --nelz <NEL> Number of voxels in the z-direction (spn)
--xmin <MIN> Minimum voxel in the x-direction
--xmax <MAX> Maximum voxel in the x-direction
--ymin <MIN> Minimum voxel in the y-direction
--ymax <MAX> Maximum voxel in the y-direction
--zmin <MIN> Minimum voxel in the z-direction
--zmax <MAX> Maximum voxel in the z-direction
-q, --quiet Pass to quiet the terminal output
-h, --help Print help
Mesh
automesh mesh --help
Creates a finite element mesh from a tessellation or segmentation
Usage: automesh mesh <COMMAND>
Commands:
hex Creates an all-hexahedral mesh from a tessellation or segmentation
tet Creates an all-tetrahedral mesh from a tessellation or segmentation
tri Creates all-triangular isosurface(s) from a tessellation or segmentation
help Print this message or the help of the given subcommand(s)
Options:
-h, --help Print help
Mesh Hex
automesh mesh hex --help
Creates an all-hexahedral mesh from a tessellation or segmentation
Usage: automesh mesh hex [OPTIONS] --input <FILE> --output <FILE> [COMMAND]
Commands:
smooth Applies smoothing to the mesh before output
help Print this message or the help of the given subcommand(s)
Options:
-i, --input <FILE> Tessellation (stl) or segmentation (npy | spn) input file
-o, --output <FILE> Mesh output file (exo | inp | mesh | stl | vtk)
-d, --defeature <NUM> Defeature clusters with less than NUM voxels
-x, --nelx <NEL> Number of voxels in the x-direction (spn)
-y, --nely <NEL> Number of voxels in the y-direction (spn)
-z, --nelz <NEL> Number of voxels in the z-direction (spn)
-r, --remove <ID>... Voxel IDs to remove from the mesh
-s, --size <VAL> Desired element size on the surface
--xscale <SCALE> Scaling (> 0.0) in the x-direction, applied before translation [default: 1]
--yscale <SCALE> Scaling (> 0.0) in the y-direction, applied before translation [default: 1]
--zscale <SCALE> Scaling (> 0.0) in the z-direction, applied before translation [default: 1]
--xtranslate <VAL> Translation in the x-direction [default: 0]
--ytranslate <VAL> Translation in the y-direction [default: 0]
--ztranslate <VAL> Translation in the z-direction [default: 0]
--metrics <FILE> Quality metrics output file (csv | npy)
-q, --quiet Pass to quiet the terminal output
-h, --help Print help
Mesh Tri
automesh mesh tri --help
Creates all-triangular isosurface(s) from a tessellation or segmentation
Usage: automesh mesh tri [OPTIONS] --input <FILE> --output <FILE> [COMMAND]
Commands:
smooth Applies smoothing to the mesh before output
help Print this message or the help of the given subcommand(s)
Options:
-i, --input <FILE> Tessellation (stl) or segmentation (npy | spn) input file
-o, --output <FILE> Mesh output file (exo | inp | mesh | stl | vtk)
-d, --defeature <NUM> Defeature clusters with less than NUM voxels
-x, --nelx <NEL> Number of voxels in the x-direction (spn)
-y, --nely <NEL> Number of voxels in the y-direction (spn)
-z, --nelz <NEL> Number of voxels in the z-direction (spn)
-r, --remove <ID>... Voxel IDs to remove from the mesh
-s, --size <VAL> Desired element size on the surface
--xscale <SCALE> Scaling (> 0.0) in the x-direction, applied before translation [default: 1]
--yscale <SCALE> Scaling (> 0.0) in the y-direction, applied before translation [default: 1]
--zscale <SCALE> Scaling (> 0.0) in the z-direction, applied before translation [default: 1]
--xtranslate <VAL> Translation in the x-direction [default: 0]
--ytranslate <VAL> Translation in the y-direction [default: 0]
--ztranslate <VAL> Translation in the z-direction [default: 0]
--metrics <FILE> Quality metrics output file (csv | npy)
-q, --quiet Pass to quiet the terminal output
-h, --help Print help
Mesh Hex Smooth
automesh mesh hex smooth --help
Applies smoothing to the mesh before output
Usage: automesh mesh hex --input <FILE> --output <FILE> smooth [OPTIONS] [COMMAND]
Commands:
remesh Applies isotropic remeshing to the mesh before output
help Print this message or the help of the given subcommand(s)
Options:
-c, --hierarchical Pass to enable hierarchical control
-n, --iterations <NUM> Number of smoothing iterations [default: 20]
-m, --method <NAME> Smoothing method (Laplace | Taubin) [default: Taubin]
-k, --pass-band <FREQ> Pass-band frequency (for Taubin only) [default: 0.1]
-s, --scale <SCALE> Scaling parameter for all smoothing methods [default: 0.6307]
-h, --help Print help
Mesh Tri Smooth
automesh mesh tri smooth --help
Applies smoothing to the mesh before output
Usage: automesh mesh tri --input <FILE> --output <FILE> smooth [OPTIONS] [COMMAND]
Commands:
remesh Applies isotropic remeshing to the mesh before output
help Print this message or the help of the given subcommand(s)
Options:
-c, --hierarchical Pass to enable hierarchical control
-n, --iterations <NUM> Number of smoothing iterations [default: 20]
-m, --method <NAME> Smoothing method (Laplace | Taubin) [default: Taubin]
-k, --pass-band <FREQ> Pass-band frequency (for Taubin only) [default: 0.1]
-s, --scale <SCALE> Scaling parameter for all smoothing methods [default: 0.6307]
-h, --help Print help
Mesh Tri Smooth Remesh
automesh mesh tri smooth remesh --help
Applies isotropic remeshing to the mesh before output
Usage: automesh mesh tri smooth remesh [OPTIONS]
Options:
-n, --iterations <NUM> Number of remeshing iterations [default: 5]
-q, --quiet Pass to quiet the terminal output
-h, --help Print help
Metrics
automesh metrics --help
Quality metrics for an existing finite element mesh
Usage: automesh metrics <COMMAND>
Commands:
hex Quality metrics for an all-hexahedral finite element mesh
tet Quality metrics for an all-tetrahedral finite element mesh
tri Quality metrics for an all-triangular finite element mesh
help Print this message or the help of the given subcommand(s)
Options:
-h, --help Print help
automesh implements the following element quality metrics:
Hexahedral Metrics
automesh metrics hex --help
Quality metrics for an all-hexahedral finite element mesh
Usage: automesh metrics hex [OPTIONS] --input <FILE> --output <FILE>
Options:
-i, --input <FILE> Mesh input file (exo | inp | stl)
-o, --output <FILE> Quality metrics output file (csv | npy)
-q, --quiet Pass to quiet the terminal output
-h, --help Print help
automesh implements the following hexahedral element quality metrics1:
- Maximum edge ratio
- Minimum scaled Jacobian
- Maximum skew
- Element volume
A brief description of each metric follows.
Maximum Edge Ratio
- measures the ratio of the longest edge to the shortest edge in a mesh element.
- A ratio of 1.0 indicates perfect element quality, whereas a very large ratio indicates bad element quality.
- Knupp et al.1 (page 87) indicate an acceptable range of
[1.0, 1.3].
Minimum Scaled Jacobian
- evaluates the determinant of the Jacobian matrix at each of the corners nodes, normalized by the corresponding edge lengths, and returns the minimum value of those evaluations.
- Interpretation
- : Perfect rectangular element
- : Element is valid (positive Jacobian)
- : Element zero volume
- : Invalid element (inverted/negative Jacobian)
Typically, mesh quality requirements specify for acceptable elements.
- Knupp et al.1 (page 92) indicate an acceptable range of
[0.5, 1.0], though in practice, minimum values as low as0.2and0.3are often used.
Figure. Illustration of minimum scaled Jacobian2 with acceptable range [0.3, 1.0].
Maximum Skew
- Skew measures how much an element deviates from being a regular shape (e.g., in 3D, a cube or regular tetrahedron; in 2D, a square or equilateral triangle). A skew value of 0 indicates a perfectly regular shape, while higher values indicate increasing levels of distortion.
- Knupp et al.1 (page 97) indicate an acceptable range of
[0.0, 0.5].
Element Volume
- Measures the volume of the element.
Unit Tests
Inspired by Figure 2 of Livesu et al.3 reproduced here below

we examine several unit test singleton elements and their metrics.
| valence | singleton | volume | |||
|---|---|---|---|---|---|
| 3 |  | 1.000000e0 (1.000) | 8.660253e-1 (0.866) | 5.000002e-1 (0.500) | 8.660250e-1 (0.866) |
| 3' (noised) |  | 1.292260e0 (2.325) ** Cubit (aspect ratio): 1.292 | 1.917367e-1 (0.192) | 6.797483e-1 (0.680) | 1.247800e0 (1.248) |
| 4 |  | 1.000000e0 (1.000) | 1.000000e0 (1.000) | 0.000000e0 (0.000) | 1.000000e0 (1.000) |
| 4' (noised) |  | 1.167884e0 (1.727) ** Cubit (aspect ratio): 1.168 | 3.743932e-1 (0.374) | 4.864936e-1 (0.486) | 9.844008e-1 (0.984) |
| 5 |  | 1.000000e0 (1.000) | 9.510566e-1 (0.951) | 3.090169e-1 (0.309) | 9.510570e-1 (0.951) |
| 6 |  | 1.000000e0 (1.000) | 8.660253e-1 (0.866) | 5.000002e-1 (0.500) | 8.660250e-1 (0.866) |
| ... | ... | ... | ... | ... | ... |
| 10 |  | 1.000000e0 (1.000) | 5.877851e-1 (0.588) | 8.090171e-1 (0.809) | 5.877850e-1 (0.588) |
Figure: Hexahedral metrics. Leading values are from automesh. Values in parenthesis are results from HexaLab.4 Items with ** indicate where automesh and Cubit agree, but HexaLab disagrees. Cubit uses the term Aspect Ratio for Edge Ratio for hexahedral elements. All values were also verified with Cubit.
The connectivity for all elements:
1, 2, 4, 3, 5, 6, 8, 7
with prototype:

The element coordinates follow:
# 3
1, 0.000000e0, 0.000000e0, 0.000000e0
2, 1.000000e0, 0.000000e0, 0.000000e0
3, -0.500000e0, 0.866025e0, 0.000000e0
4, 0.500000e0, 0.866025e0, 0.000000e0
5, 0.000000e0, 0.000000e0, 1.000000e0
6, 1.000000e0, 0.000000e0, 1.000000e0
7, -0.500000e0, 0.866025e0, 1.000000e0
8, 0.500000e0, 0.866025e0, 1.000000e0
# 3'
1, 0.110000e0, 0.120000e0, -0.130000e0
2, 1.200000e0, -0.200000e0, 0.000000e0
3, -0.500000e0, 1.866025e0, -0.200000e0
4, 0.500000e0, 0.866025e0, -0.400000e0
5, 0.000000e0, 0.000000e0, 1.000000e0
6, 1.000000e0, 0.000000e0, 1.000000e0
7, -0.500000e0, 0.600000e0, 1.400000e0
8, 0.500000e0, 0.866025e0, 1.200000e0
# 4
1, 0.000000e0, 0.000000e0, 0.000000e0
2, 1.000000e0, 0.000000e0, 0.000000e0
3, 0.000000e0, 1.000000e0, 0.000000e0
4, 1.000000e0, 1.000000e0, 0.000000e0
5, 0.000000e0, 0.000000e0, 1.000000e0
6, 1.000000e0, 0.000000e0, 1.000000e0
7, 0.000000e0, 1.000000e0, 1.000000e0
8, 1.000000e0, 1.000000e0, 1.000000e0
# 4'
1, 0.100000e0, 0.200000e0, 0.300000e0
2, 1.200000e0, 0.300000e0, 0.400000e0
3, -0.200000e0, 1.200000e0, -0.100000e0
4, 1.030000e0, 1.102000e0, -0.250000e0
5, -0.001000e0, -0.021000e0, 1.002000e0
6, 1.200000e0, -0.100000e0, 1.100000e0
7, 0.000000e0, 1.000000e0, 1.000000e0
8, 1.010000e0, 1.020000e0, 1.030000e0
# 5
1, 0.000000e0, 0.000000e0, 0.000000e0
2, 1.000000e0, 0.000000e0, 0.000000e0
3, 0.309017e0, 0.951057e0, 0.000000e0
4, 1.309017e0, 0.951057e0, 0.000000e0
5, 0.000000e0, 0.000000e0, 1.000000e0
6, 1.000000e0, 0.000000e0, 1.000000e0
7, 0.309017e0, 0.951057e0, 1.000000e0
8, 1.309017e0, 0.951057e0, 1.000000e0
# 6
1, 0.000000e0, 0.000000e0, 0.000000e0
2, 1.000000e0, 0.000000e0, 0.000000e0
3, 0.500000e0, 0.866025e0, 0.000000e0
4, 1.500000e0, 0.866025e0, 0.000000e0
5, 0.000000e0, 0.000000e0, 1.000000e0
6, 1.000000e0, 0.000000e0, 1.000000e0
7, 0.500000e0, 0.866025e0, 1.000000e0
8, 1.500000e0, 0.866025e0, 1.000000e0
# 10
1, 0.000000e0, 0.000000e0, 0.000000e0
2, 1.000000e0, 0.000000e0, 0.000000e0
3, 0.809017e0, 0.587785e0, 0.000000e0
4, 1.809017e0, 0.587785e0, 0.000000e0
5, 0.000000e0, 0.000000e0, 1.000000e0
6, 1.000000e0, 0.000000e0, 1.000000e0
7, 0.809017e0, 0.587785e0, 1.000000e0
8, 1.809017e0, 0.587785e0, 1.000000e0
Local Numbering Scheme
Nodes
The local numbering scheme for nodes of a hexahedral element:
7---------6
/| /|
/ | / |
4---------5 |
| 3------|--2
| / | /
|/ |/
0---------1
| node | connected nodes |
|---|---|
| 0 | 1, 3, 4 |
| 1 | 0, 2, 5 |
| 2 | 1, 3, 6 |
| 3 | 0, 2, 7 |
| 4 | 0, 5, 7 |
| 5 | 1, 4, 6 |
| 6 | 2, 5, 7 |
| 7 | 3, 4, 6 |
Faces
From the exterior of the element, view the (0, 1, 5, 4) face and unwarp the remaining faces; the six face normals now point out of the page. The local numbering scheme for faces of a hexahedral element:
7---------6
| |
| 5 |
| |
7---------4---------5---------6---------7
| | | | |
| 3 | 0 | 1 | 2 |
| | | | |
3---------0---------1---------2---------3
| |
| 4 |
| |
3---------2
| face | nodes |
|---|---|
| 0 | 0, 1, 5, 4 |
| 1 | 1, 2, 6, 5 |
| 2 | 2, 3, 7, 6 |
| 3 | 3, 0, 4, 7 |
| 4 | 3, 2, 1, 0 |
| 5 | 4, 5, 6, 7 |
Formulation
For a hexahedral element with eight nodes, the scaled Jacobian at each node is computed as:
where:
- , , and are edge vectors emanating from the node,
- is the cross product of the first two edge vectors, and
- denotes the Euclidean norm.
The minimum scaled Jacobian for the element is:
Node Numbering Convention
The hexahedral element uses the following local node numbering (standard convention):
7----------6
/| /|
/ | / |
4----------5 |
| | | |
| 3-------|--2
| / | /
|/ |/
0----------1
Edge Vectors at Each Node
For each node , three edge vectors are defined that point to adjacent nodes. The connectivity follows this pattern:
| Node | Edge Vector Definitions | |||
|---|---|---|---|---|
| 0 | → 1 | → 3 | → 4 | , , |
| 1 | → 2 | → 0 | → 5 | , , |
| 2 | → 3 | → 1 | → 6 | , , |
| 3 | → 0 | → 2 | → 7 | , , |
| 4 | → 7 | → 5 | → 0 | , , |
| 5 | → 4 | → 6 | → 1 | , , |
| 6 | → 5 | → 7 | → 2 | , , |
| 7 | → 6 | → 4 | → 3 | , , |
where is the position of node .
Algorithm
-
For each element in the mesh:
a. Extract the 8 node indices from the connectivity array
b. For each node :
-
Compute edge vectors: where , , are adjacent nodes per the table above
-
Compute cross product:
-
Compute scaled Jacobian:
c. Take minimum over all 8 nodes:
-
-
Return the vector of minimum scaled Jacobians, one per element
Implementation
This prototyptical Rust implementation calculates the MSJ by evaluating the Jacobian at each of the eight corners using the edges connected to that corner.
#![allow(unused)] fn main() { struct Vector3 { x: f64, y: f64, z: f64, } impl Vector3 { fn sub(a: &Vector3, b: &Vector3) -> Vector3 { Vector3 { x: a.x - b.x, y: a.y - b.y, z: a.z - b.z } } fn dot(a: &Vector3, b: &Vector3) -> f64 { a.x * b.x + a.y * b.y + a.z * b.z } fn cross(a: &Vector3, b: &Vector3) -> Vector3 { Vector3 { x: a.y * b.z - a.z * b.y, y: a.z * b.x - a.x * b.z, z: a.x * b.y - a.y * b.x, } } fn norm(&self) -> f64 { (self.x.powi(2) + self.y.powi(2) + self.z.powi(2)).sqrt() } } /// Calculates the Minimum Scaled Jacobian for a hexahedron. /// nodes: An array of 8 points ordered by standard FEM convention. pub fn min_scaled_jacobian(nodes: &[Vector3; 8]) -> f64 { // Define the three edges meeting at each of the 8 corners // Corners are ordered: 0-3 (bottom face), 4-7 (top face) // For each node index: (current_node, u_target, v_target, w_target) let corner_indices = [ (0, 1, 3, 4), // Corner 0: edges to 1, 3, 4 (1, 2, 0, 5), // Corner 1: edges to 2, 0, 5 (2, 3, 1, 6), // Corner 2: edges to 3, 1, 6 (3, 0, 2, 7), // Corner 3: edges to 0, 2, 7 (4, 7, 5, 0), // Corner 4: edges to 7, 5, 0 (5, 4, 6, 1), // Corner 5: edges to 4, 6, 1 (6, 5, 7, 2), // Corner 6: edges to 5, 7, 2 (7, 6, 4, 3), // Corner 7: edges to 6, 4, 3 ]; let mut min_sj = f64::MAX; const EPSILON: f64 = 1e-15; // Small threshold to avoid division by zero for &(curr, i, j, k) in &corner_indices { // Calculate edge vectors: u, v, w from current node let u = Vector3::sub(&nodes[i], &nodes[curr]); let v = Vector3::sub(&nodes[j], &nodes[curr]); let w = Vector3::sub(&nodes[k], &nodes[curr]); // Calculate n = u × v let n = Vector3::cross(&u, &v); // Calculate scaled Jacobian: (n · w) / (||u|| * ||v|| * ||w||) let det = Vector3::dot(&n, &w); let lengths = u.norm() * v.norm() * w.norm(); // Avoid division by zero for degenerate elements let sj = if lengths > EPSILON { det / lengths } else { f64::NEG_INFINITY // Flag completely degenerate elements }; if sj < min_sj { min_sj = sj; } } min_sj } }
Implementation Notes
The implementation evaluates all 8 nodes of each element and returns the minimum value. This ensures that element distortion at any corner is captured, as poor quality at a single node can affect finite element solution accuracy.
Node-based Refinement
Node-based refinement reframes the traditional minimum scaled Jacobian formulation, which finds a per element minimum value, as a per node weighted value calculation.
- This calculation produces the incremental movement of the subject node that would improve the scaled Jacobian for the element at that node.
- The development follows an incremental update of nodal position, similar to the update formulation of Laplace and Taubin smoothing.)
Node and Element Valence
We define nodal valence as the number of nodes connected via an element edge to the subject node. For a hexahedral mesh, the minimum nodal valence is three (for a node at an external corner of an element); the maximum nodal valence eight (for a node on the internal portion of the mesh).
We define element valence as the number of elements connected via an element connectivity to the subject node. For a hexahedral mesh, the minimum element valence is one (for a node at an external corner of an element); the maximum nodal valence is eight (for a node on the internal portion of the mesh). Let denote the element valence for a particular node.
For a given subject node with position connected to one-to-eight elements, for the element, , find the three edge-connected element nodes, located at position , and . We assume the node numbering convention given above, with
Figure: A general hexahedral element in .
Figure: A dextral, orthogonal local reference frame created from three nodes , , and that share edge connectivity with common node . The location of is the location of that creates a scaled Jacobian of unity.
The current scaled Jacobian is defined by the current location of , holding positions of , constant:
From this definition, we define an ideal nodal position that exactly produces a scaled Jacobian of unity:
The ideal position is a point such that the vectors , , and are mutually orthogonal. How can we solve for in terms of , , and ?
We solve for by assuring that the three right triangles formed by and combinations of , , and satisfy Pythagorean's theorem. Let lengths
Then Pythagorean's theorem requires
This represents a system of three independent equations and three unknowns , , and .
Subtracting Eq. (18) from Eq. (17) and solving,
Figure: Vectors , , and that sequentially connect points , and .
Before proceeding, we can further simplify the expressions of these equations by defining edge vectors that connect each of the points , , and that circle the path on . Let
Note that the square values of each of the three hypotenuses is , , and , respectively. Then
Solving,
The lengths , , and are now known. It is also known that in the local , , coordinate system spanned by the right-handed, orthonormal triad , , at point , the lengths , , , with their corresponding components of , , define the three components of , that is,
Weighting (aka Voting)
Any scheme for weighting of the connected elements can be adopted. Perhaps elements that lie on the surface should be given greater weighting than elements that lie on the interior. The effect would be to create higher quality element near the surface, and relatively lower quality element would be pushed into the interior of the volume. For a given element in the element valence of node , ,
For now, however, let's just explore the equal weighting scheme:
This is just the average of all ideal locations for each connected element .
Iteration
We define a gap vector as originating at the current position and terminating at the current ideal nodal position :
The quantity is geometrically interpreted as a search direction or gap vector, analogous to the gap vector defined for Laplace smoothing.
Let be the positive scaling factor for the gap .
Since
subdivision of this relationship into several substeps gives rise to an iterative approach. We typically select to avoid overshoot of the update, .
At iteration , we update the position of by an amount to as
with
Thus
and finally considering equal weighting for all connected elements
Sign Check
Because the derivation of finding involves squared terms, we must take one additional precaution to assure that the search direction is opposite the direction of the face normal of .
Let the face normal be defined as the cross product of any two edges of , e.g.,
In general, and are not colinear (they are colinear only for the special case where all lengths , , are equal). Nonetheless, for a non-inverted element with the search direction in the opposite direction of the face normal , the sign function (sgn) is used,
If an inverted element is encountered such that , then Eq. (39) should be modified to reverse the direction of , viz.
Compare the in Eq. (39) to the in Eq. (42).
References
-
Knupp PM, Ernst CD, Thompson DC, Stimpson CJ, Pebay PP. The verdict geometric quality library. SAND2007-1751. Sandia National Laboratories (SNL), Albuquerque, NM, and Livermore, CA (United States); 2006 Mar 1. link ↩ ↩2 ↩3 ↩4
-
Hovey CB. Naval Force Health Protection Program Review 2023 Presentation Slides. SAND2023-05198PE. Sandia National Lab.(SNL-NM), Albuquerque, NM (United States); 2023 Jun 26. link ↩
-
Livesu M, Pitzalis L, Cherchi G. Optimal dual schemes for adaptive grid based hexmeshing. ACM Transactions on Graphics (TOG). 2021 Dec 6;41(2):1-4. link ↩
-
Bracci M, Tarini M, Pietroni N, Livesu M, Cignoni P. HexaLab.net: An online viewer for hexahedral meshes. Computer-Aided Design. 2019 May 1;110:24-36. link ↩
Tetrahedral Metrics
automesh metrics tet --help
Quality metrics for an all-tetrahedral finite element mesh
Usage: automesh metrics tet [OPTIONS] --input <FILE> --output <FILE>
Options:
-i, --input <FILE> Mesh input file (exo | inp | stl)
-o, --output <FILE> Quality metrics output file (csv | npy)
-q, --quiet Pass to quiet the terminal output
-h, --help Print help
automesh implements the following tetrahedral element quality metrics1:
- Maximum edge ratio
- Minimum scaled Jacobian
- Maximum skew
- Element volume
A brief description of each metric follows.
Maximum Edge Ratio
- measures the ratio of the longest edge to the shortest edge in a mesh element.
- A ratio of 1.0 indicates perfect element quality, whereas a very large ratio indicates bad element quality.
- Knupp et al.1 (page 63) indicate an acceptable range of
[1.0, 3.0].
Minimum Scaled Jacobian
- evaluates the determinant of the Jacobian matrix at each of the corners nodes (and the Jacobian itself1 page 71), normalized by the corresponding edge lengths, and returns the minimum value of those evaluations.
- Knupp et al.1 (page 75) indicate an acceptable range of
[0.5, sqrt(2)/2][0.5, 0.707]. - A scaled Jacobian close to
0indicates that the tetrahedra is poorly shaped (e.g., very thin or degenerate), which can lead to numerical instability. - A scaled Jacobian of
1indicates that the tetrahedra is equilateral, which is the ideal shape for numerical methods.
Maximum Skew
- Skew measures how much an element deviates from being a regular shape (e.g., in 3D a cube or a regular tetrahedron; in 2D a square or equilateral triangle). A skew value of 0 indicates a perfectly regular shape, while higher values indicate increasing levels of distortion.
- Knupp et al.1 does not give a definition of skew for tetrahedra, so we provide our definition below. For any triangle composing the four faces of a tetrahedron, where is the smallest angle of the triangle,
- The maximum skew of a tetrahedron is the maximum skew of all of the four triangular faces (see Triangular Metrics, Maximum Skew).
- For an equilateral (regular) tetrahedron, and .
- In the limit as .
Element Volume
- Measures the volume of the element (see Knupp et al.1, page 61).
Unit Tests
We verify the following element qualities:
| tetrahedron | volume | |||
|---|---|---|---|---|
| simple | 1.225 | 0.843 [0.843] | 0.197 | 0.167 [0.167] |
| right-handed | 1.414 | 0.707 [0.707] | 0.250 | 0.167 [0.167] |
| left-handed | 1.414 | -0.707 [-0.707] | 0.250 | -0.167 [-0.167] |
| degenerate | 3.33 | 0.000 [0.000] | 0.637 | 0.000 [0.000] |
| random | 2.086 | 0.208 [0.208] | 0.619 | 0.228 [0.228] |
| regular | 1.000 | 1.000 [1.000] | 0.000 | 2.667 [2.667] |
Figure: Tetrahedral metrics. Leading values are from automesh. All values agree with an independent Python calculation, (see metrics_tetrahedral.py) in double precision with a tolerance of less than 1.00e-14. Values in [brackets], minimum scaled Jacobian and volume, also agree with Cubit. Cubit does not compute edge ratio and skew for tetrahedral elements. Cubit uses the term Aspect Ratio; it is not the same as Edge Ratio.
Figure: Python visualization of the tetrahedron test cases, created with metrics_tetrahedral.py.
Local Numbering Scheme
Nodes
The local numbering scheme for nodes of a tetrahedral element:
3
/|\
L3 / | \ L5
/ | \
0---|---2 (horizontal line is L2)
\ | /
L0 \ | / L1
\|/
1
(vertical line is L4)
where
L0 = p1 - p0 L3 = p3 - p0
L1 = p2 - p1 L4 = p3 - p1
L3 = p0 - p2 L5 = p3 - p2
| node | connected nodes |
|---|---|
| 0 | 1, 2, 3 |
| 1 | 0, 2, 3 |
| 2 | 0, 1, 3 |
| 3 | 0, 1, 2 |
Faces
A tetrahedron has four triangular faces. The faces are typically numbered opposite to the node they do not contain (e.g., face 0 is opposite to node 0).
From the exterior of the element, view the (0, 1, 3) face and upwarp the remaining faces; the four face normals now point out out of the page. The local numbering scheme for faces of a tetrahedral element:
2-------3-------2
\ 1 / \ 0 /
\ / \ /
\ / 2 \ /
0-------1
\ 3 /
\ /
\ /
2
| face | nodes |
|---|---|
| 0 | 1, 2, 3 |
| 1 | 0, 2, 3 |
| 2 | 0, 1, 3 |
| 3 | 0, 1, 2 |
Source
metrics_tetrahedral.py
"""Visualize various tetrahedra and calculate quality metrics."""
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.art3d import Poly3DCollection
from typing import List, Tuple
def calculate_edge_vectors(nodes: np.ndarray) -> List[np.ndarray]:
"""Calculate the six edge vectors of a tetrahedron.
Args:
nodes (np.ndarray): A 2D numpy array of shape (4, 3)
representing the coordinates of the four nodes
of the tetrahedron.
Returns:
List[np.ndarray]: A list containing six 1D numpy arrays, each
representing an edge vector.
"""
# Base edges (in a cycle 0 -> 1 -> 2 -> 0)
e0 = nodes[1] - nodes[0] # n1 - n0
e1 = nodes[2] - nodes[1] # n2 - n1
e2 = nodes[0] - nodes[2] # n0 - n2
# Edges connecting the apex (node 3)
e3 = nodes[3] - nodes[0] # n3 - n0
e4 = nodes[3] - nodes[1] # n3 - n1
e5 = nodes[3] - nodes[2] # n3 - n2
return [e0, e1, e2, e3, e4, e5]
def signed_element_volume(nodes: np.ndarray) -> float:
"""Calculate the signed volume of a tetrahedron.
Args:
nodes (np.ndarray): A 2D numpy array of shape (4, 3)
representing the coordinates of the four nodes
of the tetrahedron.
Returns:
float: The signed volume of the tetrahedron.
"""
v0, v1, v2, v3 = nodes
return np.dot(np.cross(v1 - v0, v2 - v0), v3 - v0) / 6.0
def maximum_edge_ratio(nodes: np.ndarray) -> float:
"""Calculate the maximum edge ratio (max_length / min_length) of a tetrahedron.
Args:
nodes (np.ndarray): A 2D numpy array of shape (4, 3)
representing the coordinates of the four nodes
of the tetrahedron.
Returns:
float: The maximum edge ratio. Returns `float('inf')` if the minimum
edge length is zero.
"""
edge_vectors = calculate_edge_vectors(nodes)
lengths = [np.linalg.norm(v) for v in edge_vectors]
min_length = min(lengths)
max_length = max(lengths)
if min_length == 0:
return float("inf")
return float(max_length / min_length)
def minimum_scaled_jacobian(nodes: np.ndarray) -> float:
"""Calculate the minimum scaled Jacobian quality metric for a tetrahedron.
Args:
nodes (np.ndarray): A 2D numpy array of shape (4, 3)
representing the coordinates of the four nodes
of the tetrahedron.
Returns:
float: The minimum scaled Jacobian value. Returns 0.0 if the maximum
nodal Jacobian is zero.
"""
# The element Jacobian j is 6.0 times the signed element volume
j = signed_element_volume(nodes) * 6.0
# Get all six edge lengths
edge_vectors = calculate_edge_vectors(nodes)
els = [np.linalg.norm(v) for v in edge_vectors]
# Compute the four nodal Jacobians
lambda_0 = els[0] * els[2] * els[3]
lambda_1 = els[0] * els[1] * els[4]
lambda_2 = els[1] * els[2] * els[5]
lambda_3 = els[3] * els[4] * els[5]
# Find the maximum of the nodal Jacobians (including the element Jacobian)
lambda_max = max([j, lambda_0, lambda_1, lambda_2, lambda_3])
# Calculate the final quality metric
if lambda_max == 0.0:
return 0.0 # Avoid division by zero for collapsed elements
else:
return j * np.sqrt(2.0) / lambda_max
def face_minimum_angle(
nodes: np.ndarray, n0_idx: int, n1_idx: int, n2_idx: int
) -> float:
"""Calculate the minimum angle of a triangular face.
Args:
nodes (np.ndarray): A 2D numpy array of shape (4, 3)
representing the coordinates of the four nodes
of the tetrahedron.
n0_idx (int): Index of the first node of the face.
n1_idx (int): Index of the second node of the face.
n2_idx (int): Index of the third node of the face.
Returns:
float: The minimum angle (in radians) of the triangular face.
"""
v0 = nodes[n0_idx]
v1 = nodes[n1_idx]
v2 = nodes[n2_idx]
l0 = v2 - v1
l1 = v0 - v2
l2 = v1 - v0
# Normalize
l0 = l0 / np.linalg.norm(l0)
l1 = l1 / np.linalg.norm(l1)
l2 = l2 / np.linalg.norm(l2)
flip = -1.0
angles = [
np.arccos(np.clip(np.dot(l0 * flip, l1), -1.0, 1.0)),
np.arccos(np.clip(np.dot(l1 * flip, l2), -1.0, 1.0)),
np.arccos(np.clip(np.dot(l2 * flip, l0), -1.0, 1.0)),
]
return min(angles)
def face_maximum_skew(
nodes: np.ndarray, n0_idx: int, n1_idx: int, n2_idx: int
) -> float:
"""Calculate the maximum skew for a single triangular face of a tetrahedron.
Args:
nodes (np.ndarray): A 2D numpy array of shape (4, 3)
representing the coordinates of the four nodes
of the tetrahedron.
n0_idx (int): Index of the first node of the face.
n1_idx (int): Index of the second node of the face.
n2_idx (int): Index of the third node of the face.
Returns:
float: The maximum skew value for the triangular face.
"""
tolerance = 1e-9
equilateral_rad = np.pi / 3.0 # 60 degrees in radians
minimum_angle = face_minimum_angle(nodes, n0_idx, n1_idx, n2_idx)
if abs(equilateral_rad - minimum_angle) < tolerance:
return 0.0
else:
return (equilateral_rad - minimum_angle) / equilateral_rad
def maximum_skew(nodes: np.ndarray) -> float:
"""Calculate the maximum skew across all four faces of the tetrahedron.
Args:
nodes (np.ndarray): A 2D numpy array of shape (4, 3)
representing the coordinates of the four nodes
of the tetrahedron.
Returns:
float: The maximum skew value among all faces of the tetrahedron.
"""
# A tetrahedron has four faces, so calculate the skew for each and
# then take the maximum
skews = [
face_maximum_skew(nodes, 0, 1, 2),
face_maximum_skew(nodes, 0, 1, 3),
face_maximum_skew(nodes, 0, 2, 3),
face_maximum_skew(nodes, 1, 2, 3),
]
return max(skews)
def visualize_tetrahedron(
nodes: np.ndarray,
title: str = "Tetrahedron",
show_edges: bool = True,
show_labels: bool = True,
save_figure: bool = False,
) -> Tuple[plt.Figure, plt.Axes]:
"""Visualize a tetrahedron given its four node coordinates and display quality metrics.
Args:
nodes (np.ndarray): A 2D numpy array of shape (4, 3)
representing the coordinates of the four nodes
of the tetrahedron.
title (str, optional): Title for the plot. Defaults to "Tetrahedron".
show_edges (bool, optional): Whether to display the edges of the tetrahedron.
Defaults to True.
show_labels (bool, optional): Whether to display labels for the nodes.
Defaults to True.
save_figure (bool, optional): Whether to save the figure as a PNG file.
Defaults to False.
Returns:
Tuple[plt.Figure, plt.Axes]: A tuple containing the matplotlib Figure and Axes objects.
"""
nodes = np.array(nodes)
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection="3d")
# Define the four faces of the tetrahedron
# Each face is a triangle defined by three nodes
faces = [
[nodes[0], nodes[1], nodes[2]], # Face 0-1-2
[nodes[0], nodes[1], nodes[3]], # Face 0-1-3
[nodes[0], nodes[2], nodes[3]], # Face 0-2-3
[nodes[1], nodes[2], nodes[3]], # Face 1-2-3
]
# Create the 3D polygon collection for faces
face_collection = Poly3DCollection(
faces, alpha=0.3, facecolor="lightblue", edgecolor="blue", linewidths=1.5
)
ax.add_collection3d(face_collection)
# Plot nodes
ax.scatter(
nodes[:, 0],
nodes[:, 1],
nodes[:, 2],
c="navy",
s=100,
marker="o",
edgecolors="black",
linewidths=2,
)
# Add node labels
if show_labels:
for i, node in enumerate(nodes):
ax.text(
node[0], node[1], node[2], f" n{i}", fontsize=12, fontweight="bold"
)
# Draw edges if requested
if show_edges:
edges = [
(0, 1),
(1, 2),
(2, 0), # Base triangle
(0, 3),
(1, 3),
(2, 3), # Edges to apex
]
for edge in edges:
points = nodes[list(edge)]
ax.plot3D(*points.T, "b-", linewidth=2, alpha=0.6)
# Calculate all metrics
volume = signed_element_volume(nodes)
max_edge_ratio = maximum_edge_ratio(nodes)
min_scaled_jac = minimum_scaled_jacobian(nodes)
max_skew = maximum_skew(nodes)
# Set labels and title
ax.set_xlabel("x", fontsize=12)
ax.set_ylabel("y", fontsize=12)
ax.set_zlabel("z", fontsize=12)
title_text = f"{title}\n"
title_text += f"Max Edge Ratio: {max_edge_ratio:.6f}, "
title_text += f"Min Scaled Jacobian: {min_scaled_jac:.6f}\n"
title_text += f"Max Skew: {max_skew:.6f}, "
title_text += f"Volume: {volume:.6f}"
ax.set_title(title_text, fontsize=12, fontweight="bold")
# Set equal aspect ratio
max_range = (
np.array(
[
nodes[:, 0].max() - nodes[:, 0].min(),
nodes[:, 1].max() - nodes[:, 1].min(),
nodes[:, 2].max() - nodes[:, 2].min(),
]
).max()
/ 2.0
)
mid_x = (nodes[:, 0].max() + nodes[:, 0].min()) * 0.5
mid_y = (nodes[:, 1].max() + nodes[:, 1].min()) * 0.5
mid_z = (nodes[:, 2].max() + nodes[:, 2].min()) * 0.5
ax.set_xlim(mid_x - max_range, mid_x + max_range)
ax.set_ylim(mid_y - max_range, mid_y + max_range)
ax.set_zlim(mid_z - max_range, mid_z + max_range)
# ax.view_init(elev=63, azim=-110, roll=0)
ax.view_init(elev=18, azim=-57, roll=0)
ax.set_aspect("equal")
plt.tight_layout()
if save_figure:
filename = title.replace(" ", "_").lower() + ".png"
plt.savefig(filename, dpi=300)
print(f"Saved figure to {filename}")
return fig, ax
# Example 1: Simple tetrahedron
NAME = "Simple Tetrahedron"
print(f"Example 1: {NAME}")
nodes_1 = np.array(
[
[0.0, 0.0, 0.0],
[1.0, 0.0, 0.0],
[0.5, 1.0, 0.0],
[0.5, 0.5, 1.0],
]
)
visualize_tetrahedron(nodes_1, NAME, save_figure=True)
# Example 2: Positive signed volume (right-handed)
NAME = "Right-Handed Tetrahedron"
print(f"\nExample 2: {NAME}")
nodes_2 = np.array(
[
[0.0, 0.0, 0.0],
[1.0, 0.0, 0.0],
[0.0, 1.0, 0.0],
[0.0, 0.0, 1.0],
]
)
visualize_tetrahedron(nodes_2, NAME, save_figure=True)
# Example 3: Negative signed volume (left-handed / inverted)
NAME = "Left-Handed Tetrahedron"
print(f"\nExample 3: {NAME}")
nodes_3 = np.array(
[
[0.0, 0.0, 0.0],
[1.0, 0.0, 0.0], # Node 1
[0.0, 1.0, 0.0], # Node 2
[0.0, 0.0, 1.0], # Node 3
]
)
# Connectivity is [0, 2, 1, 3] - swapped nodes 1 and 2
nodes_3_inverted = nodes_3[[0, 2, 1, 3]]
visualize_tetrahedron(nodes_3_inverted, NAME, save_figure=True)
# Example 4: Degenerate tetrahedron (zero volume)
NAME = "Degenerate Tetrahedron"
print(f"\nExample 4: {NAME}")
nodes_4 = np.array(
[
[0.0, 0.0, 0.0],
[1.0, 0.0, 0.0],
[0.0, 1.0, 0.0],
[0.3, 0.3, 0.0], # Co-planar with other nodes
]
)
visualize_tetrahedron(nodes_4, NAME, save_figure=True)
# Example 5: Random tetrahedron
NAME = "Random Tetrahedron"
print(f"\nExample 5: {NAME}")
nodes_5 = np.array(
[
[0.5, 0.5, 0.5],
[1.8, 0.2, 1.1],
[0.1, 1.5, 0.3],
[1.3, 1.9, 2.0],
]
)
visualize_tetrahedron(nodes_5, NAME, save_figure=True)
# Example 6: Regular tetrahedron (for maximum skew test, has zero skew)
NAME = "Regular Tetrahedron"
print(f"\nExample 6: {NAME}")
nodes_6 = np.array(
[
[0.0, 0.0, 2.0],
[2.0, 0.0, 0.0],
[0.0, 2.0, 0.0],
[2.0, 2.0, 2.0],
]
)
visualize_tetrahedron(nodes_6, NAME, save_figure=True)
plt.show()
References
-
Knupp PM, Ernst CD, Thompson DC, Stimpson CJ, Pebay PP. The verdict geometric quality library. SAND2007-1751. Sandia National Laboratories (SNL), Albuquerque, NM, and Livermore, CA (United States); 2006 Mar 1. link ↩ ↩2 ↩3 ↩4 ↩5 ↩6
Triangular Metrics
automesh metrics tri --help
Quality metrics for an all-triangular finite element mesh
Usage: automesh metrics tri [OPTIONS] --input <FILE> --output <FILE>
Options:
-i, --input <FILE> Mesh input file (exo | inp | stl)
-o, --output <FILE> Quality metrics output file (csv | npy)
-q, --quiet Pass to quiet the terminal output
-h, --help Print help
automesh implements the following triangular element quality metrics1:
- Maximum edge ratio
- Minimum scaled Jacobian
- Maximum skew
- Element area
- Minimum angle
A brief description of each metric follows.
Maximum Edge Ratio
- measures the ratio of the longest edge to the shortest edge in a mesh element.
- A ratio of 1.0 indicates perfect element quality, whereas a very large ratio indicates bad element quality.
- Knupp et al.1 (page 26) indicate an acceptable range of
[1.0, 1.3].
Minimum Scaled Jacobian
- evaluates the determinant of the Jacobian matrix at each of the corners nodes, normalized by the corresponding edge lengths, and returns the minimum value of those evaluations.
- Knupp et al.1 (page 29) indicate an acceptable range of
[0.5, 2*sqrt(3)/3][0.5, 1.2]. - A scaled Jacobian close to
0indicates that the triangle is poorly shaped (e.g., very thin or degenerate), which can lead to numerical instability. - A scaled Jacobian of
1indicates that the triangle is equilateral, which is the ideal shape for numerical methods. This is achieved through scaling as follows:
- In the preceeding equation,
- is the smallest angle of an equilateral triangle, and
- is the smallest angle of the subject triangle.
Maximum Skew
- Skew measures how much an element deviates from being a regular shape (e.g., in 3D a cube or a regular tetrahedron; in 2D a square or equilateral triangle). A skew value of 0 indicates a perfectly regular shape, while higher values indicate increasing levels of distortion.
- Knupp et al.1 does not give a definition of skew for triangles, so we provide our definition below. For a triangle where is the smallest angle of the triangle,
- For an equilateral triangle, and .
- In the limit as .
Element Area
- Measures the area of the element.
Minimum Angle
- The smallest the three angles of a triangle.
- Ideal value: (for an equilateral triangle).
- The should be maximized (kept as close to as possible) and above a minimum threshold (e.g., to ).
- Acute angles (close to ) cause high errors and numerical instability.
Unit Tests
We use the ABAQUS input file single_valence_04_noise2.inp.
We import the file into Cubit and create a triangular surface mesh:
import abaqus mesh geometry "/Users/chovey/autotwin/automesh/tests/input/single_valence_04_noise2.inp" feature_angle 135.00
surface 1 scheme trimesh minimum size 100
surface 2 scheme trimesh minimum size 100
surface 3 scheme trimesh minimum size 100
surface 4 scheme trimesh minimum size 100
surface 5 scheme trimesh minimum size 100
# surface 6 scheme trimesh minimum size 100 # there is no side 6, two sides were merged
delete mesh surface all propagate
surface all scheme trimesh
mesh surface all
quality tri all aspect ratio global draw mesh list detail
quality tri all scaled jacobian global draw mesh list detail
quality tri all element area global draw mesh list detail
export stl ascii "/Users/chovey/autotwin/automesh/tests/input/single_valence_04_noise2.stl" mesh overwrite
We also examine several .stl files and process them, for example,
import stl "/Users/chovey/autotwin/automesh/tests/input/one_facet.stl" feature_angle 135.00 merge make_elements
surface 1 scheme trimesh minimum size 100
delete mesh surface 1 propagate
surface 1 scheme trimesh
mesh surface 1
quality tri all aspect ratio global draw mesh list detail
quality tri all scaled jacobian global draw mesh list detail
quality tri all element area global draw mesh list detail
We verify the following element qualities:
| file | e | area | (deg) | |||
|---|---|---|---|---|---|---|
A | 1 | 1.508 [1.508] | 0.761 [0.761] | 0.313 [0.331] | 0.610 [0.610] | 41.2 [41.2] |
A | 2 | 1.550 [1.550] | 0.739 [0.739] | 0.337 [0.337] | 0.550 [0.550] | 39.8 [39.8] |
A | 3 | 1.787 [1.787] | 0.639 [0.639] | 0.440 [0.440] | 0.569 [0.569] | 33.6 [33.6] |
A | 4 | 1.915 [1.915] | 0.595 [0.595] | 0.483 [0.483] | 0.402 [0.402] | 31.0 [31.0] |
A | 5 | 2.230 [2.230] | 0.426 [0.426] | 0.639 [0.639] | 0.342 [0.342] | 21.7 [21.7] |
A | 6 | 1.623 [1.623] | 0.700 [0.700] | 0.378 [0.378] | 0.571 [0.571] | 37.3 [37.1] |
A | 7 | 1.240 [1.240] | 0.898 [0.898] | 0.149 [0.149] | 0.424 [0.424] | 51.0 [51.0] |
A | 8 | 1.385 [1.385] | 0.831 [0.831] | 0.233 [0.233] | 0.443 [0.443] | 46.1 [46.1] |
A | 9 | 1.606 [1.606] | 0.719 [0.719] | 0.358 [0.358] | 0.648 [0.648] | 38.5 [38.5] |
A | 10 | 1.429 [1.429] | 0.806 [0.806] | 0.262 [0.262] | 0.704 [0.704] | 44.3 [44.3] |
A | 11 | 1.275 [1.275] | 0.880 [0.880] | 0.172 [0.172] | 0.668 [0.668] | 49.7 [49.7] |
A | 12 | 1.436 [1.436] | 0.804 [0.804] | 0.264 [0.264] | 0.516 [0.516] | 44.1 [44.1] |
B | 1 | 1.414 [1.414] | 0.816 [0.816] | 0.250 [0.250] | 0.500 [0.500] | 45.0 [45.0] |
C | 1 | 1.000 [1.000] | 1.000 [1.000] | 0.000 [0.000] | 6.928 [6.928] | 60.0 [60.0] |
D | 1 | 1.000 [1.000] | 1.000 [1.000] | 0.000 [0.000] | 0.433 [0.433] | 60.0 [60.0] |
E | 1 | 1.256 [1.256] | 0.869 [0.869] | 0.187 [0.187] | 3.273 [3.273] | 48.8 [48.8] |
Figure: Triangle metrics.
Leading values are from automesh.
Values in [brackets] are from an independent Python calculation, (see metrics_triangular.py) and agree with automesh in double precision with a tolerance of less than 2.22e-15.
Except for edge ratio, all values were also verified with Cubit.
Cubit uses the term Aspect Ratio; it is not the same as Edge Ratio.
- File
Aissingle_valence_04_noise2.inp. - File
Bisone_facet.stl. - File
Cis an equilateral triangle with nodal coordinates at(-2, 0, 0),(2, 0, 0), and(0, 2*sqrt(3), 0)and has side length4.0, saved totests/input/equilateral_4.stl. - File
Dis an equilateral triangle with nodal coordinates at(-0.5, 0, 0),(0.5, 0, 0), and(0, sqrt(3) / 2, 0)and has side length1.0, saved totests/input/equilateral_1.stl. - File
Eis an off axis triangle with approximate (30, 60, 90) degree inner angles, with coordinates at(0.0, 1.0, 3.0),(2.0, 0.0, 2.0), and(1.0, sqrt(3.0) + 1.0, 1.0), saved totests/input/off_axis.stl. eis the element number in the mesh.
Local Numbering Scheme
Nodes
The local numbering scheme for nodes of a triangular element:
2
/ \
/ \
/ \
/ \
0---------1
| node | connected nodes |
|---|---|
| 0 | 1, 2 |
| 1 | 0, 2 |
| 2 | 0, 1 |
Faces
The local numbering scheme for faces of a triangular element:
| face | nodes |
|---|---|
| 0 | 0, 1, 2 |
Source
metrics_triangular.py
"""This script is a quality control tool for the metrics of a tri mesh."""
from typing import Final
import numpy as np
DEG_TO_RAD: Final[float] = np.pi / 180.0
J_EQUILATERAL: Final[float] = np.sqrt(3.0) / 2.0 # sin(60 deg)
def nf(x):
"""Does a list comprehension, casting each item from a np.float64
to a float."""
return [float(y) for y in x]
nodal_coordinates = (
(-0.2, 1.2, -0.1), # single_valence_04_noise2.inp begin
(1.180501, 0.39199, 0.3254445),
(0.1, 0.2, 0.3),
(-0.001, -0.021, 1.002),
(1.2, -0.1, 1.1),
(1.03, 1.102, -0.25),
(0.0, 1.0, 1.0),
(1.01, 1.02, 1.03), # single_valence_04_noise2.inp end
(0.0, 0.0, 1.0), # one_facet.stl begin
(0.0, 0.0, 0.0),
(1.0, 0.0, 0.0), # one_facet.stl end
(-2.0, 0.0, 0.0), # equilateral with edge length 4.0 start
(2.0, 0.0, 0.0),
(0.0, 2.0 * np.sqrt(3.0), 0.0), # equilateral with edge length 4.0 end
(-0.5, 0.0, 0.0), # equilateral with edge length 1.0 start
(0.5, 0.0, 0.0),
(0.0, np.sqrt(3.0) / 2.0, 0.0), # equilateral with edge length 1.0 end
(0.0, 1.0, 3.0), # off_axis.stl begin
(2.0, 0.0, 2.0),
(1.0, np.sqrt(3.0) + 1.0, 1.0), # off_axis.stl end
)
element_node_connectivity = (
(1, 2, 3), # single_valence_04_noise2.inp begin
(4, 2, 5),
(1, 6, 2),
(4, 3, 2),
(4, 1, 3),
(4, 7, 1),
(2, 8, 5),
(6, 8, 2),
(7, 8, 6),
(1, 7, 6),
(4, 5, 8),
(7, 4, 8), # single_valence_04_noise2.inp end
(9, 10, 11), # one_facet.stl
(12, 13, 14), # equilateral triangle with side length 4.0
(15, 16, 17), # equilateral triangle with side length 1.0
(18, 19, 20), # off_axis.stl
)
NODE_NUMBERING_OFFSET: Final[int] = 1
mesh_element_max_edge_lengths = []
mesh_element_edge_ratios = []
mesh_element_minimum_angles = []
mesh_element_maximum_skews = []
mesh_element_areas = []
mesh_element_jacobians = []
mesh_element_jacobians_scaled = []
def angle(a: np.ndarray, b: np.ndarray) -> float:
"""Given two vectors, find the angle between them."""
dot_product = np.dot(a, b)
norm_a = np.linalg.norm(a)
norm_b = np.linalg.norm(b)
cos_theta = dot_product / (norm_a * norm_b)
angle_radians = np.arccos(cos_theta)
result = np.degrees(angle_radians) # degrees
return result
for element in element_node_connectivity:
print(f"element with nodes: {element}")
path = element + (element[0],)
# print(f" node path {path}")
pairs = tuple(zip(element, element[1:] + (element[0],)))
print(f" node pairs {pairs}")
element_edge_ratios = []
element_minimum_angles = []
element_minimum_jacobians = []
edge_vectors = ()
# edge ratios
for pair in pairs:
print(f" pair {pair}")
aa, bb = pair
edge = np.array(nodal_coordinates[bb - NODE_NUMBERING_OFFSET]) - np.array(
nodal_coordinates[aa - NODE_NUMBERING_OFFSET]
)
edge_vectors = edge_vectors + (edge,)
edge_length = np.linalg.norm(edge)
# print(f" lens {edge_length}")
element_edge_ratios.append(edge_length)
# print(f" edge ratios {element_edge_ratios}")
# edge ratios
len_max = max(element_edge_ratios)
# print(f" max edge ratio {len_max}")
mesh_element_max_edge_lengths.append(len_max)
len_min = min(element_edge_ratios)
# print(f" min edge ratio {len_min}")
ratio = len_max / len_min
mesh_element_edge_ratios.append(ratio)
# edge vectors and then angles
edge_vectors_pairs = tuple(zip(edge_vectors, edge_vectors[1:] + (edge_vectors[0],)))
# print(f" edge vectors pairs {edge_vectors_pairs}")
for item in edge_vectors_pairs:
# print(f" edge vectors pair {item}")
# flip the direction of the first vector so that it shares an origin
# with the secon vector
angle_degrees = angle(-1.0 * item[0], item[1])
# print(f" angle {angle_degrees}")
element_minimum_angles.append(angle_degrees)
print(f" element angles (deg) {nf(element_minimum_angles)}")
angle_min = min(element_minimum_angles)
print(f" min angle (deg) {angle_min}")
mesh_element_minimum_angles.append(angle_min)
jacobian_e = np.sin(angle_min * DEG_TO_RAD)
jacobian_scaled_e = jacobian_e / J_EQUILATERAL
print(f" min Jacobian (sin(angle_min)) {jacobian_e}")
print(f" min scaled Jacobian {jacobian_scaled_e}")
mesh_element_jacobians.append(jacobian_e)
mesh_element_jacobians_scaled.append(jacobian_scaled_e)
skew_max = (60.0 - angle_min) / 60.0
mesh_element_maximum_skews.append(skew_max)
# Compute areas only for triangles for now.
if len(element) == 3:
# area of a triangle
aa = np.linalg.norm(edge_vectors[0])
bb = np.linalg.norm(edge_vectors[1])
cc = np.linalg.norm(edge_vectors[2])
# Calculate the semi-perimeter
ss = (aa + bb + cc) / 2.0
# Use Heron's formula to calcuate the area
area = np.sqrt(ss * (ss - aa) * (ss - bb) * (ss - cc))
mesh_element_areas.append(area)
print(f"\nmesh element max edge lengths: {nf(mesh_element_max_edge_lengths)}")
print(f"\nmesh element edge ratios: {nf(mesh_element_edge_ratios)}")
print(f"\nmesh element minimum angles: {nf(mesh_element_minimum_angles)}")
print(f"\nmesh element maximum skews: {nf(mesh_element_maximum_skews)}")
print(f"\nmesh element areas: {nf(mesh_element_areas)}")
print(f"\nmesh minimum scaled Jacobians: {nf(mesh_element_jacobians_scaled)}")
References
-
Knupp PM, Ernst CD, Thompson DC, Stimpson CJ, Pebay PP. The verdict geometric quality library. SAND2007-1751. Sandia National Laboratories (SNL), Albuquerque, NM, and Livermore, CA (United States); 2006 Mar 1. link ↩ ↩2 ↩3 ↩4
Remesh
automesh remesh --help
Applies isotropic remeshing to an existing mesh
Usage: automesh remesh [OPTIONS] --input <FILE> --output <FILE>
Options:
-i, --input <FILE> Mesh input file (exo | inp | stl)
-o, --output <FILE> Mesh output file (exo | mesh | stl | vtk)
-n, --iterations <NUM> Number of remeshing iterations [default: 5]
-q, --quiet Pass to quiet the terminal output
-h, --help Print help
Segment
automesh segment --help
Creates a segmentation or voxelized mesh from an existing mesh
Usage: automesh segment <COMMAND>
Commands:
hex Segments an all-hexahedral mesh
tet Segments an all-tetrahedral mesh
tri Segments an all-triangular mesh
help Print this message or the help of the given subcommand(s)
Options:
-h, --help Print help
Segment Hex
automesh segment hex --help
Segments an all-hexahedral mesh
Usage: automesh segment hex [OPTIONS] --input <FILE> --output <FILE> --size <NUM>
Options:
-i, --input <FILE> Mesh input file (exo | inp)
-o, --output <FILE> Segmentation (npy | spn) or mesh (exo | inp) output file
-g, --grid <NUM> Grid length for sampling within each element [default: 1]
-s, --size <NUM> Element size which is the side length
-r, --remove <ID>... Block IDs to remove from the mesh
-q, --quiet Pass to quiet the terminal output
-h, --help Print help
Segment Tet
automesh segment tet --help
Segments an all-tetrahedral mesh
Usage: automesh segment tet [OPTIONS] --input <FILE> --output <FILE> --size <NUM>
Options:
-i, --input <FILE> Mesh input file (exo | inp)
-o, --output <FILE> Segmentation (npy | spn) or mesh (exo | inp) output file
-g, --grid <NUM> Grid length for sampling within each element [default: 1]
-s, --size <NUM> Element size which is the side length
-r, --remove <ID>... Block IDs to remove from the mesh
-q, --quiet Pass to quiet the terminal output
-h, --help Print help
Segment Tri
automesh segment tri --help
Segments an all-triangular mesh
Usage: automesh segment tri [OPTIONS] --input <FILE> --output <FILE> --size <NUM>
Options:
-i, --input <FILE> Mesh input file (exo | inp)
-o, --output <FILE> Segmentation (npy | spn) or mesh (exo | inp) output file
-g, --grid <NUM> Grid length for sampling within each element [default: 1]
-s, --size <NUM> Element size which is the side length
-r, --remove <ID>... Block IDs to remove from the mesh
-q, --quiet Pass to quiet the terminal output
-h, --help Print help
Sample Points
The input mesh is queried for its material composition for
--grid 1: at a single discrete sample point located at the center of a voxel,--grid 2: at eight discrete sample points located in a2x2x2arrangement within subdivided cells of the voxel,--grid 3: at 27 discrete sample points located within a3x3x3arrangement within subdivided cells of the voxel,- and so on.
The --grid and --size options are illustrated below for three successive grid sizes:
Smooth
automesh smooth --help
Applies smoothing to an existing mesh
Usage: automesh smooth <COMMAND>
Commands:
hex Smooths an all-hexahedral mesh
tet Smooths an all-tetrahedral mesh
tri Smooths an all-triangular mesh
help Print this message or the help of the given subcommand(s)
Options:
-h, --help Print help
Smooth Hex
automesh smooth hex --help
Smooths an all-hexahedral mesh
Usage: automesh smooth hex [OPTIONS] --input <FILE> --output <FILE> [COMMAND]
Commands:
remesh Applies isotropic remeshing to the mesh before output
help Print this message or the help of the given subcommand(s)
Options:
-c, --hierarchical Pass to enable hierarchical control
-i, --input <FILE> Mesh input file (exo | inp)
-o, --output <FILE> Smoothed mesh output file (exo | inp | mesh | vtk)
-n, --iterations <NUM> Number of smoothing iterations [default: 20]
-m, --method <NAME> Smoothing method (Laplace | Taubin) [default: Taubin]
-k, --pass-band <FREQ> Pass-band frequency (for Taubin only) [default: 0.1]
-s, --scale <SCALE> Scaling parameter for all smoothing methods [default: 0.6307]
--metrics <FILE> Quality metrics output file (csv | npy)
-q, --quiet Pass to quiet the terminal output
-h, --help Print help
Smooth Tri
automesh smooth tri --help
Smooths an all-triangular mesh
Usage: automesh smooth tri [OPTIONS] --input <FILE> --output <FILE> [COMMAND]
Commands:
remesh Applies isotropic remeshing to the mesh before output
help Print this message or the help of the given subcommand(s)
Options:
-c, --hierarchical Pass to enable hierarchical control
-i, --input <FILE> Mesh input file (exo | inp | stl)
-o, --output <FILE> Smoothed mesh output file (exo | inp | mesh | stl | vtk)
-n, --iterations <NUM> Number of smoothing iterations [default: 20]
-m, --method <NAME> Smoothing method (Laplace | Taubin) [default: Taubin]
-k, --pass-band <FREQ> Pass-band frequency (for Taubin only) [default: 0.1]
-s, --scale <SCALE> Scaling parameter for all smoothing methods [default: 0.6307]
--metrics <FILE> Quality metrics output file (csv | npy)
-q, --quiet Pass to quiet the terminal output
-h, --help Print help
Smooth Tri Remesh
automesh smooth tri remesh --help
Applies isotropic remeshing to the mesh before output
Usage: automesh smooth tri --input <FILE> --output <FILE> remesh [OPTIONS]
Options:
-n, --iterations <NUM> Number of remeshing iterations [default: 5]
-q, --quiet Pass to quiet the terminal output
-h, --help Print help
Analysis
This section contains analysis that is used to answer questions pertaining to mesh creation, quality, resolution, and convergence.
Sphere with Shells
This section presents a model composed of a sphere with two concentric shells. We use the model to explore answers to the following questions:
- What compute time is required to create successively refined resolutions in
automesh? - What compute time is required to create these same resolutions in Sculpt?
- Given a rotational boundary condition, what are the displacement and strain fields for the voxel mesh?
- How do the results for the voxel mesh compare with the results for a conforming mesh?
- To what degree may smoothing the voxel mesh improve the results?
- To what degree may dualization of the voxel mesh improve the results?
Model
Python is used to create a segmentations, saved as .npy files, and visualize the results.
Given
Given three concentric spheres of radius 10, 11, and 12 cm, as shown in the figure below,
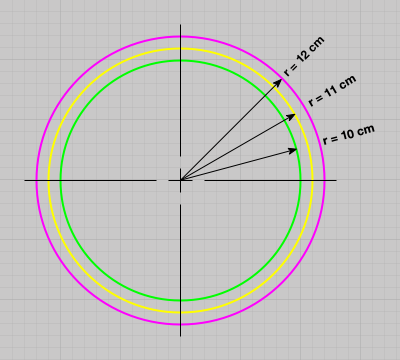
Figure: Schematic cross-section of three concentric spheres of radius 10, 11, and 12 cm. Grid spacing is 1 cm.
Find
Use segmentation resolutions 1, 2, 4, and 10 voxels per centimeter
with a cubic domain (nelx = nely = nelz) to create finite element meshes.
Solution
| vox/cm | element side length (cm) | nelx | # voxels | segmentation | file size |
|---|---|---|---|---|---|
| 1 | 1.0 | 24 | 13,824 | spheres_resolution_1.npy | 14 kB |
| 2 | 0.5 | 48 | 110,592 | spheres_resolution_2.npy | 111 kB |
| 4 | 0.25 | 96 | 884,736 | spheres_resolution_3.npy | 885 kB |
| 10 | 0.1 | 240 | 13,824,000 | spheres_resolution_4.npy | 13.78 MB |
Python Segmentation
The Python code used to generate the figures is included below.
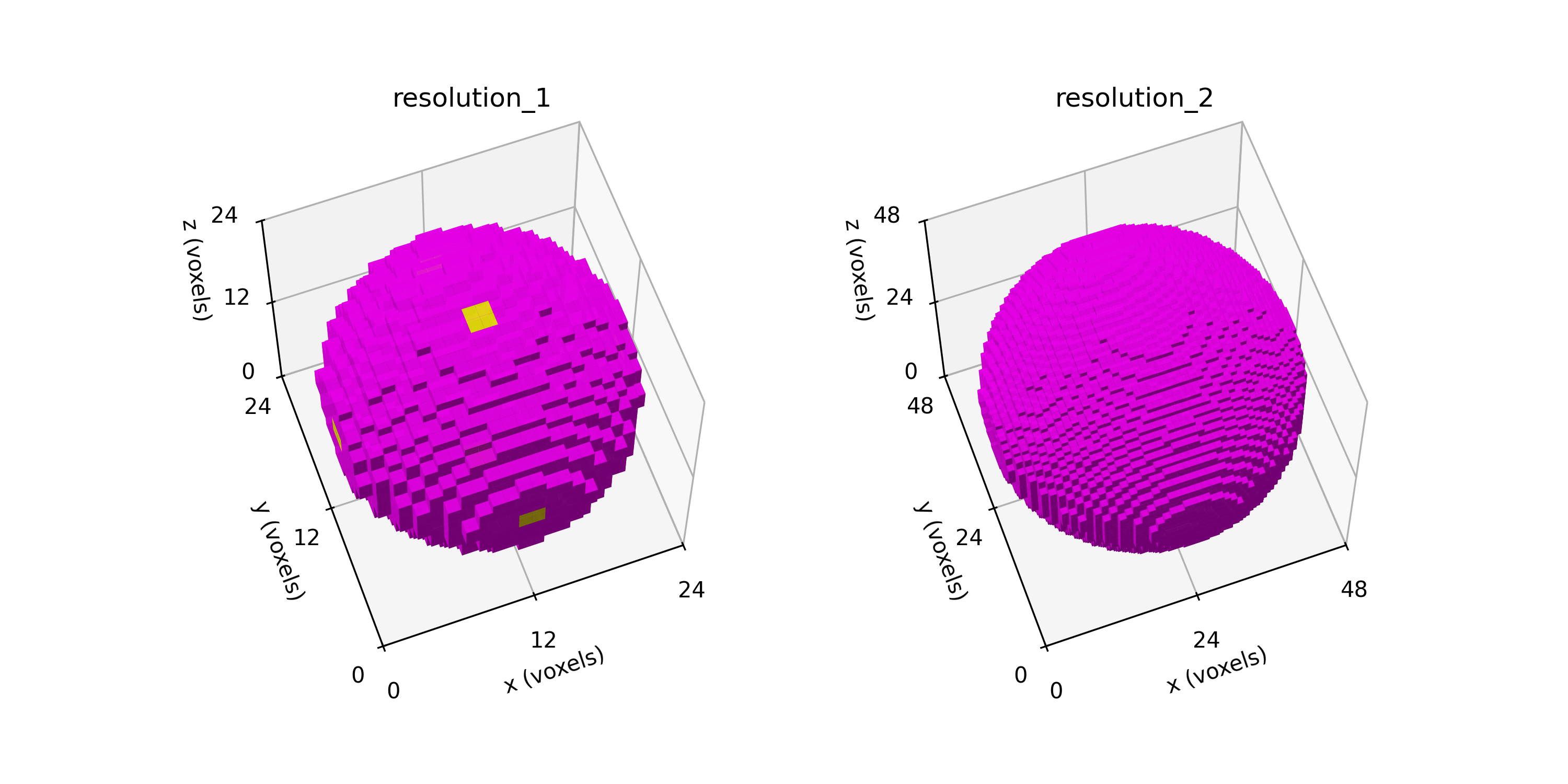
Figure: Sphere segmentations (left) spheres_resolution_1.npy and (right) spheres_resolution_2.npy shown in the voxel domain.
Because plotting large domains with Matplotlib
is slow, only the first two resolutions are shown.
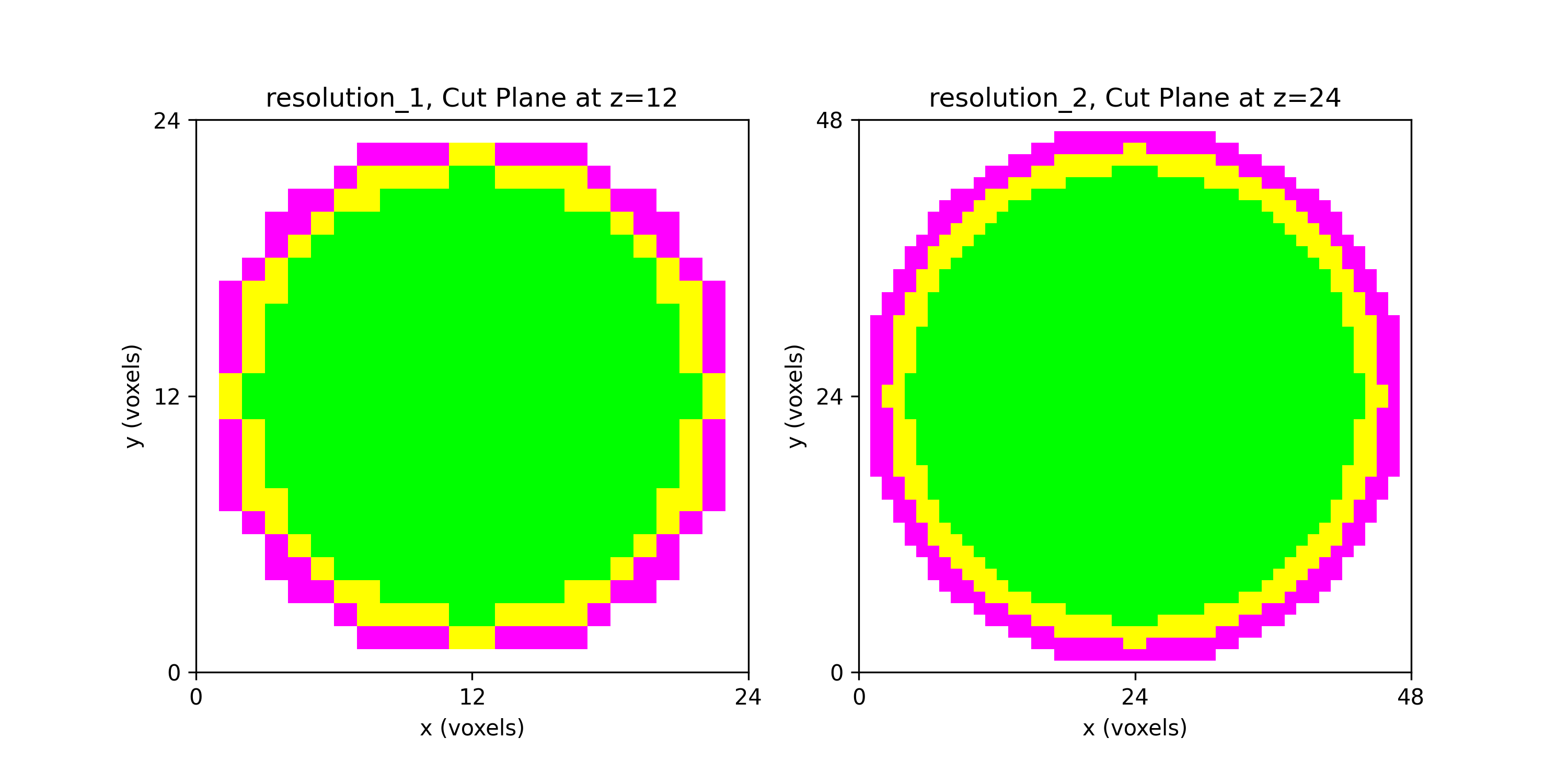
Figure: Sphere segmentations with cutting plane of (left) spheres_resolution_1.npy and (right) spheres_resolution_2.npy.
Source
spheres_cont.py
r"""This module, spheres_cont.py, builds on the spheres.py module to create
high resolution, three-material, concentric spheres and export the
voxelization as a .npy file.
Example
-------
source ~/autotwin/automesh/.venv/bin/activate
python spheres_cont.py
Output
------
~/autotwin/automesh/book/analysis/sphere_with_shells/spheres_resolution_1.npy
~/autotwin/automesh/book/analysis/sphere_with_shells/spheres_resolution_2.npy
~/autotwin/automesh/book/analysis/sphere_with_shells/spheres_resolution_3.npy
~/autotwin/automesh/book/analysis/sphere_with_shells/spheres_resolution_4.npy
"""
from pathlib import Path
from typing import Final
from matplotlib.colors import LightSource, ListedColormap
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
# Visualize on a cutting plane
def plot_cutting_plane(ax, key, data, plane="z", index=None, cmap=None, alpha=None):
"""Plots a 2D cutting plane slice of a 3D dataset on the specified axis.
This function visualizes a slice of the 3D data array along a specified
plane (x, y, or z) and displays it using a 2D image representation. The
slice can be specified by an index, and the appearance of the plot can be
customized with a colormap and transparency level.
Parameters
----------
ax : matplotlib.axes.Axes
The axes on which to plot the cutting plane.
key : str
A descriptive label for the dataset, used in the plot title.
data : numpy.ndarray
A 3D numpy array representing the voxelized data. The shape of the
array should be (depth, height, width) corresponding to the
z, y, and x dimensions.
plane : str, optional
The plane along which to slice the data. Can be 'x', 'y', or 'z'.
Default is 'z'.
index : int, optional
The index of the slice to visualize along the specified plane. If not
provided, the function will default to the middle slice of the data
along the specified plane.
cmap : str or matplotlib.colors.Colormap, optional
The colormap to use for visualizing the slice. If not provided,
defaults to 'gray'.
alpha : float, optional
The transparency level of the plotted slice, where 0 is fully
transparent and 1 is fully opaque. If not provided, defaults to 0.8.
Returns
-------
None
This function does not return any value. It modifies the provided axes
to display the cutting plane visualization.
Notes
-----
The function sets the x and y labels based on the specified plane and
adjusts the plot title to include the key and the index of the slice.
"""
origin = "lower"
if cmap is None:
cmap = "gray"
if alpha is None:
alpha = 0.8
if plane == "z":
if index is None:
index = data.shape[2] // 2 # Middle slice
slice_data = data[:, :, index]
ax.imshow(
slice_data,
cmap=cmap,
extent=[0, data.shape[1], 0, data.shape[0]],
origin=origin,
alpha=alpha,
)
ax.set_title(f"{key}, Cut Plane at z={index}")
ax.set_xlabel("x (voxels)")
ax.set_ylabel("y (voxels)")
elif plane == "y":
if index is None:
index = data.shape[1] // 2 # Middle slice
slice_data = data[:, index, :]
ax.imshow(
slice_data,
cmap=cmap,
extent=[0, data.shape[2], 0, data.shape[0]],
origin=origin,
alpha=alpha,
)
ax.set_title(f"{key}, Cut Plane at y={index}")
ax.set_xlabel("x (voxels)")
ax.set_ylabel("z (voxels)")
elif plane == "x":
if index is None:
index = data.shape[0] // 2 # Middle slice
slice_data = data[index, :, :]
ax.imshow(
slice_data,
cmap=cmap,
extent=[0, data.shape[2], 0, data.shape[1]],
origin=origin,
alpha=alpha,
)
ax.set_title(f"{key} Cut Plane at x={index}")
ax.set_xlabel("y (voxels)")
ax.set_ylabel("z (voxels)")
def sphere(resolution: int, dtype=np.uint8) -> np.ndarray:
"""Generate a 3D voxelized representation of three concentric spheres
of 10, 11, and 12 cm, at a given resolution.
Parameters
----------
resolution : int
The resolution as voxels per centimeter. Minimum value is 1.
dtype: data-type, optional
The data type of the output array. Default is np.uint8.
Returns
-------
np.ndarray
A 3D numpy array representing the voxelized spheres. Voxels within
the inner sphere are set to 1, the intermediate shell are set to 2,
and the outer shell are set to 3. Voxels outside the spheres are
set to 0.
Raises
------
ValueError
If the resolution is less than 1.
"""
print(f"Creating sphere with resolution: {resolution}")
if resolution < 1:
raise ValueError("Resolution must be >= 1")
r10 = 10 # cm
r11 = 11 # cm
r12 = 12 # cm
# We change the algorithm a bit here so we can exactly match the radius:
# number of voxels per side length (nvps)
# nvps = 2 * r12 * resolution + 1
nvps = 2 * r12 * resolution
vox_z, vox_y, vox_x = np.mgrid[
-r12 : r12 : nvps * 1j,
-r12 : r12 : nvps * 1j,
-r12 : r12 : nvps * 1j,
]
domain = vox_x**2 + vox_y**2 + vox_z**2
# sphere with radius 10, indicated with "1" and background as "0"
mask_10_in = np.array(domain <= r10 * r10, dtype=dtype) # segmentation "1"
# sphere with radius 11, indicated with "1" and background as "0"
mask_11_in = np.array(domain <= r11 * r11, dtype=dtype)
# sphere with radius 12, indicated with "1" and background as "0"
mask_12_in = np.array(domain <= r12 * r12, dtype=dtype)
mask_10_11 = mask_11_in - mask_10_in # intermediate shell
mask_11_12 = mask_12_in - mask_11_in # outer shell
# mask_10_in is already the inner sphere, segmentation "1"
shell_10_11 = 2 * mask_10_11 # intermediate shell, segmentation "2"
shell_11_12 = 3 * mask_11_12 # outer shell, segmentation "3"
result = mask_10_in + shell_10_11 + shell_11_12
print(f"Completed: Sphere with resolution: {resolution}")
return result
def main():
"""The main program."""
# rr = (1, 2, 4, 10) # resolutions (voxels per cm)
rr = (1, 2) # resolutions (voxels per cm)
lims = tuple(map(lambda x: [0, 24 * x], rr)) # limits
tt = tuple(map(lambda x: [0, 12 * x, 24 * x], rr)) # ticks
# User input begin
spheres = {
f"resolution_{i + 1}": sphere(resolution=res) for i, res in enumerate(rr)
}
aa = Path(__file__)
# Visualize the elements.
width, height = 10, 5
# width, height = 8, 4
# width, height = 6, 3
fig = plt.figure(figsize=(width, height))
fig2 = plt.figure(figsize=(width, height))
el, az, roll = 63, -110, 0
VOXEL_ALPHA: Final[float] = 0.9
CUT_ALPHA: Final[float] = 1.0
lightsource = LightSource(azdeg=325, altdeg=45) # azimuth, elevation
# lightsource = LightSource(azdeg=325, altdeg=90) # azimuth, elevation
DPI: Final[int] = 300 # resolution, dots per inch
SHOW: Final[bool] = True # turn to True to show the figure on screen
SAVE: Final[bool] = True # turn to True to save .png and .npy files
# Define the custom colormap
# Define the color mapping
# 0: transparent (no color), 1: green, 2: yellow
colors = [
(1, 1, 1, 0), # Transparent for segmentation "0"
(0, 1, 0, 1), # Green for segmentation "1"
(1, 1, 0, 1), # Yellow for segmentation "2"
(1, 0, 1, 1), # Magenta for segmentation "3"
]
custom_cmap = ListedColormap(colors)
# User input end
N_SUBPLOTS = len(spheres)
for index, (key, value) in enumerate(spheres.items()):
if SHOW:
print(f"index: {index}")
print(f"key: {key}")
# print(f"value: {value}")
ax = fig.add_subplot(1, N_SUBPLOTS, index + 1, projection=Axes3D.name)
# Create an array for face colors based on the values in the
# `value` array
facecolors = np.empty(
value.shape + (4,), dtype=float
) # Shape (x, y, z, 4) for RGBA
for i in range(value.shape[0]):
for j in range(value.shape[1]):
for k in range(value.shape[2]):
facecolors[i, j, k] = colors[value[i, j, k]]
ax.voxels(
value,
facecolors=facecolors,
# facecolors=colors[3], # outer shell color
# edgecolor=colors[3], # outer shell color
# edgecolor="black", # for better visibility
alpha=VOXEL_ALPHA,
lightsource=lightsource,
)
ax.set_title(key)
# Set labels for the axes
ax.set_xlabel("x (voxels)")
ax.set_ylabel("y (voxels)")
ax.set_zlabel("z (voxels)")
ax.set_xticks(ticks=tt[index])
ax.set_yticks(ticks=tt[index])
ax.set_zticks(ticks=tt[index])
ax.set_xlim(lims[index])
ax.set_ylim(lims[index])
ax.set_zlim(lims[index])
# Set the camera view
ax.set_aspect("equal")
ax.view_init(elev=el, azim=az, roll=roll)
if SAVE: # save the .npy segmentation output
cc = aa.with_stem("spheres_" + key)
dd = cc.with_suffix(".npy")
# Save the data in .npy format
np.save(dd, value)
print(f"Saved: {dd}")
# fig.tight_layout() # don't use as it clips the x-axis label
if SHOW:
plt.show()
if SAVE: # save the .png output
bb = aa.with_suffix(".png")
fig.savefig(bb, dpi=DPI)
print(f"Saved: {bb}")
# Plot along a cutting plane
if SHOW:
for index, (key, value) in enumerate(spheres.items()):
print(f"index: {index}")
print(f"key: {key}")
ax2 = fig2.add_subplot(1, N_SUBPLOTS, index + 1)
# Plot a cutting plane (for example, at the middle of the z-axis)
plot_cutting_plane(
ax2,
key,
value,
plane="z",
index=value.shape[2] // 2,
cmap=custom_cmap,
alpha=CUT_ALPHA,
)
ax2.set_xticks(ticks=tt[index])
ax2.set_yticks(ticks=tt[index])
ax2.set_xlim(lims[index])
ax2.set_ylim(lims[index])
plt.show()
if SAVE:
# overwrite
cc = aa.with_stem(aa.stem + "_cut").with_suffix(".png")
fig2.savefig(cc, dpi=DPI)
print(f"Saved: {cc}")
if __name__ == "__main__":
main()
Voxel Mesh with automesh
Mesh Creation
Use automesh to convert the segmentations into finite element meshes.
Remark: In the analysis below, we use the Exodus II output format (.exo) instead of the Abaqus output format (.inp). The Exodus format results in faster mesh creation and smaller file size due to compression.
Resolution 1
automesh mesh hex -i spheres_resolution_1.npy \
-o spheres_resolution_1.exo \
--remove 0 \
--xtranslate -12 --ytranslate -12 --ztranslate -12
automesh 0.3.3
Reading spheres_resolution_1.npy
Done 5.410958ms [4 materials, 13824 voxels]
Meshing voxels into hexes [xtranslate: -12, ytranslate: -12, ztranslate: -12]
Done 513.125µs [3 blocks, 6272 elements, 7563 nodes]
Writing spheres_resolution_1.exo
Done 9.939916ms
Total 16.381583ms
Resolution 2
automesh mesh hex -i spheres_resolution_2.npy \
-o spheres_resolution_2.exo \
--remove 0 \
--xscale 0.5 --yscale 0.5 --zscale 0.5 \
--xtranslate -12 --ytranslate -12 --ztranslate -12
automesh 0.3.3
Reading spheres_resolution_2.npy
Done 513.25µs [4 materials, 110592 voxels]
Meshing voxels into hexes [xscale: 0.5, yscale: 0.5, zscale: 0.5, xtranslate: -12, ytranslate: -12, ztranslate: -12]
Done 4.492458ms [3 blocks, 54088 elements, 59375 nodes]
Writing spheres_resolution_2.exo
Done 8.687541ms
Total 16.362625ms
Resolution 3
automesh mesh hex -i spheres_resolution_3.npy \
-o spheres_resolution_3.exo \
--remove 0 \
--xscale 0.25 --yscale 0.25 --zscale 0.25 \
--xtranslate -12 --ytranslate -12 --ztranslate -12
automesh 0.3.3
Reading spheres_resolution_3.npy
Done 14.784291ms [4 materials, 884736 voxels]
Meshing voxels into hexes [xscale: 0.25, yscale: 0.25, zscale: 0.25, xtranslate: -12, ytranslate: -12, ztranslate: -12]
Done 27.708125ms [3 blocks, 448680 elements, 470203 nodes]
Writing spheres_resolution_3.exo
Done 33.148125ms
Total 94.863584ms
Resolution 4
automesh mesh hex -i spheres_resolution_4.npy \
-o spheres_resolution_4.exo \
--remove 0 \
--xscale 0.1 --yscale 0.1 --zscale 0.1 \
--xtranslate -12 --ytranslate -12 --ztranslate -12
automesh 0.3.3
Reading spheres_resolution_4.npy
Done 2.846917ms [4 materials, 13824000 voxels]
Meshing voxels into hexes [xscale: 0.1, yscale: 0.1, zscale: 0.1, xtranslate: -12, ytranslate: -12, ztranslate: -12]
Done 430.685042ms [3 blocks, 7145880 elements, 7281019 nodes]
Writing spheres_resolution_4.exo
Done 464.796625ms
Total 1.119838875s
Visualization
Cubit is used for the visualizations with the following recipe:
reset
cd "/Users/chovey/autotwin/automesh/book/analysis/sphere_with_shells"
import mesh "spheres_resolution_1.exo" lite
graphics scale on
graphics clip off
view iso
graphics clip on plane location 0 -1.0 0 direction 0 1 0
view up 0 0 1
view from 100 -100 100
graphics clip manipulation off
view bottom
| resolution | 1 vox/cm | 2 vox/cm | 4 vox/cm | 10 vox/cm |
|---|---|---|---|---|
| midline | 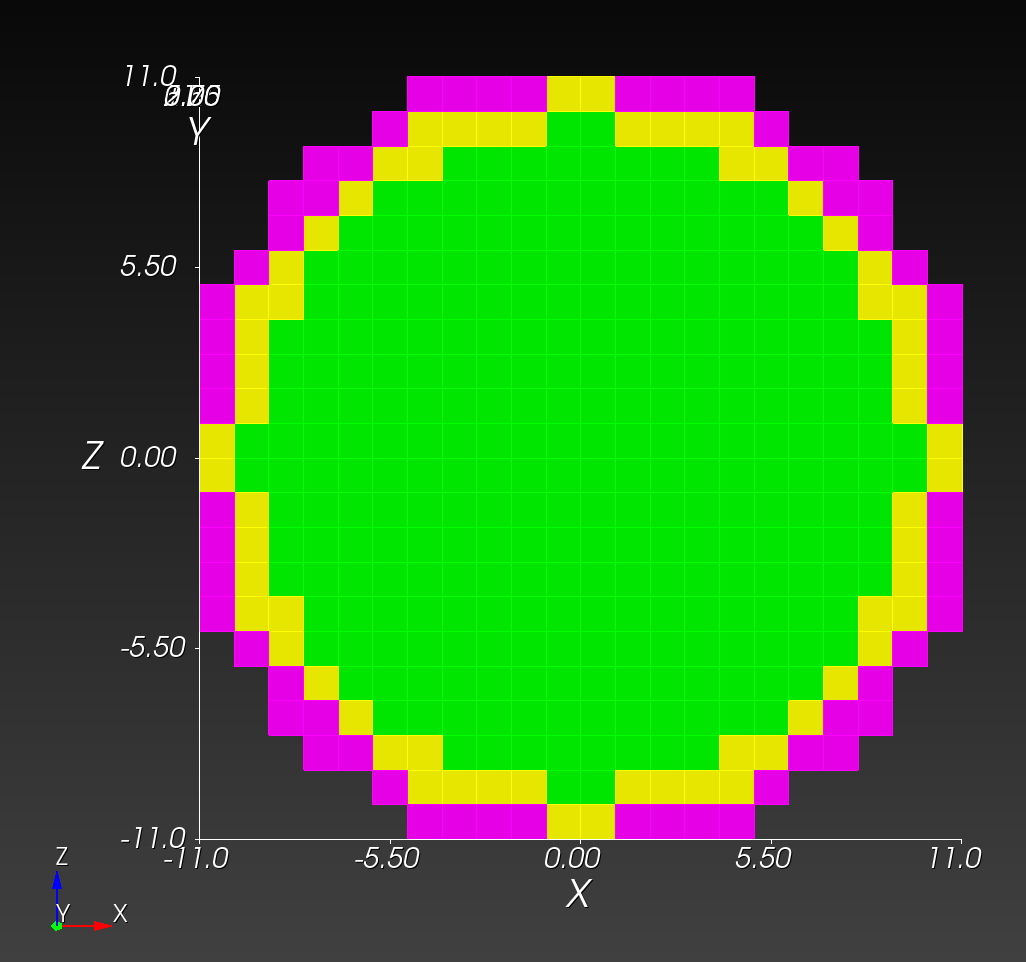 | 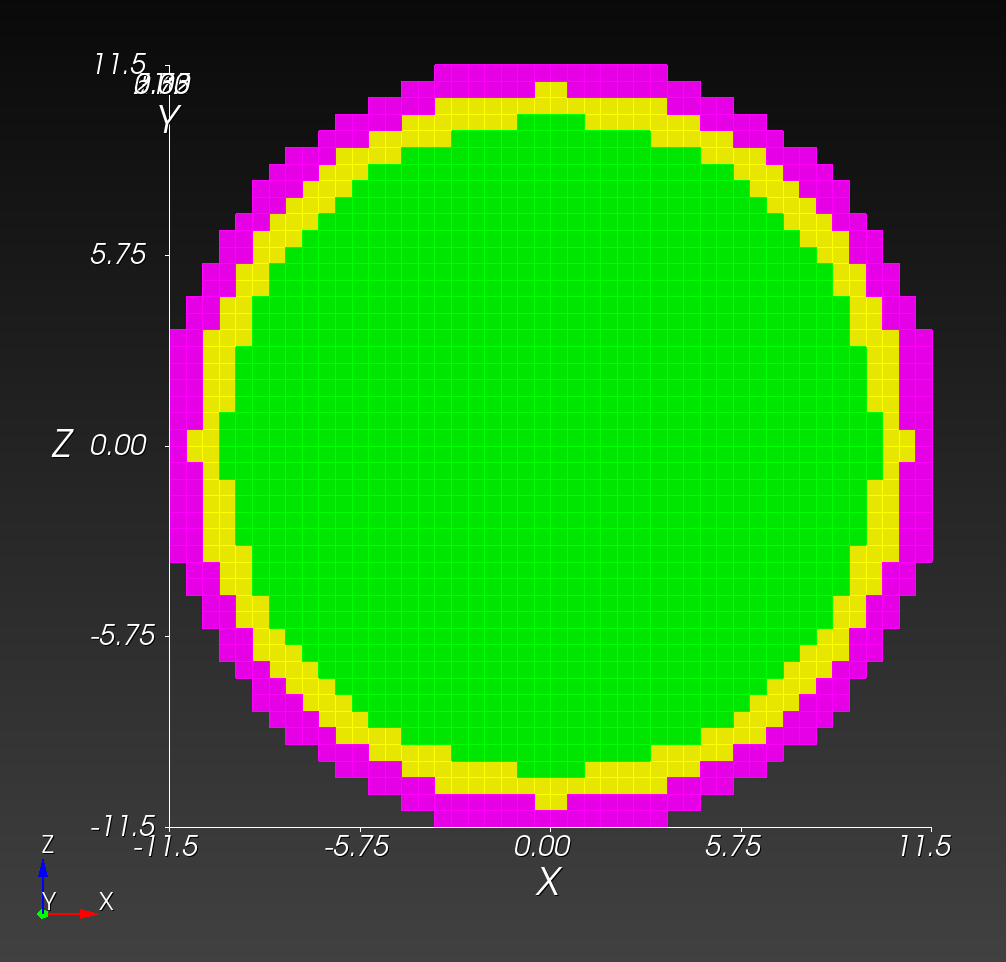 | 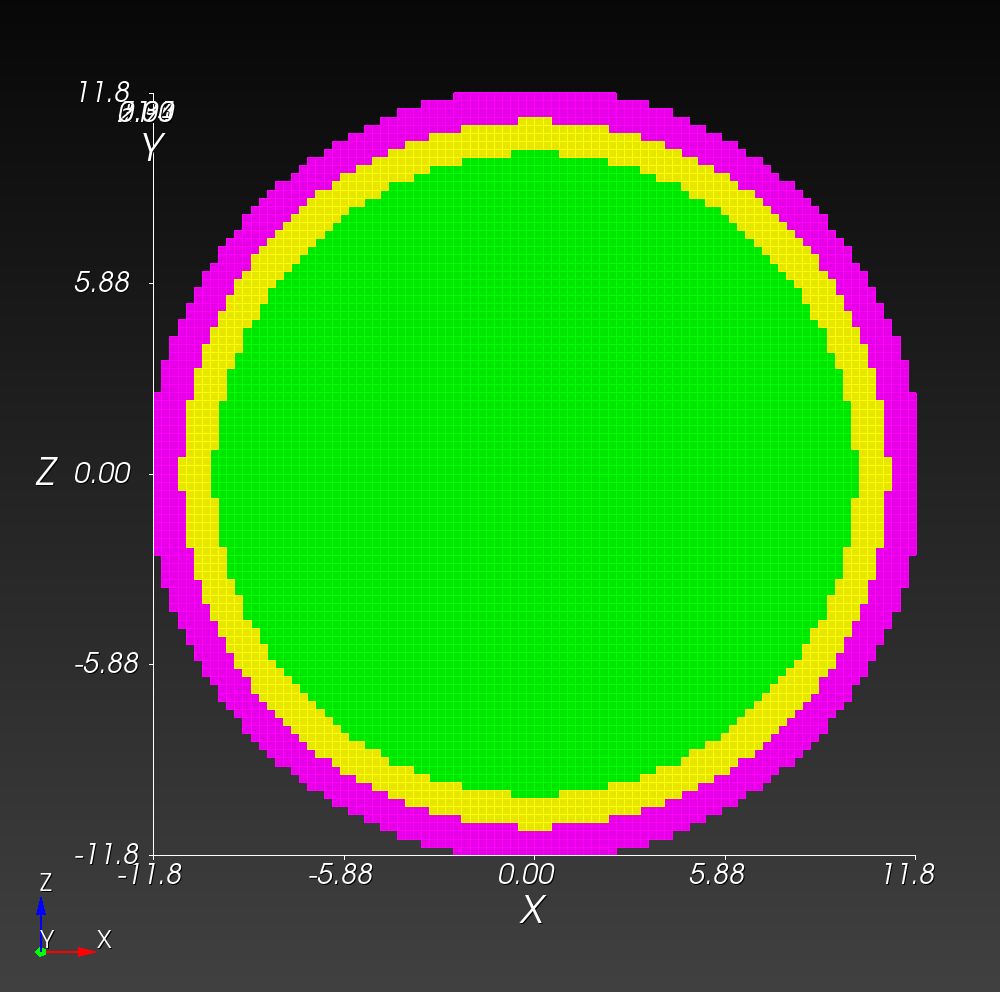 | 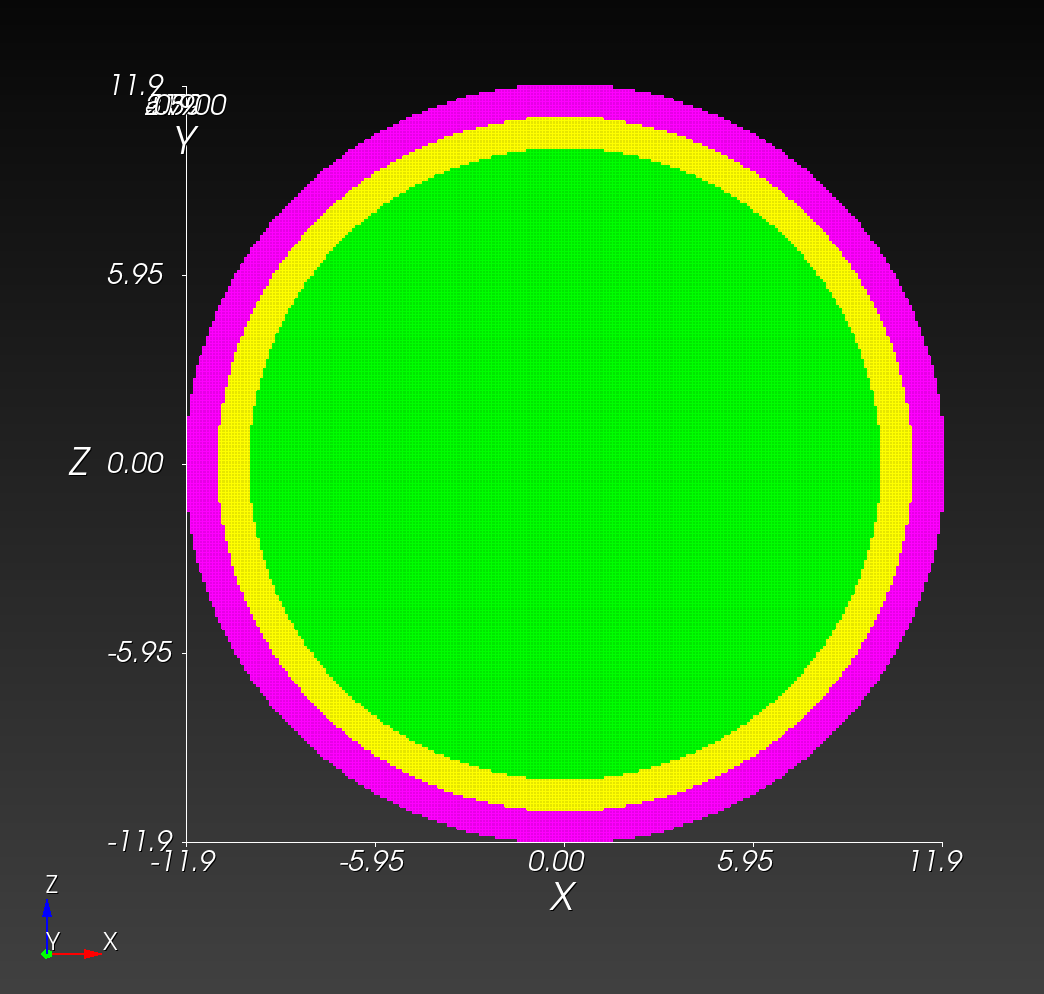 |
| isometric | 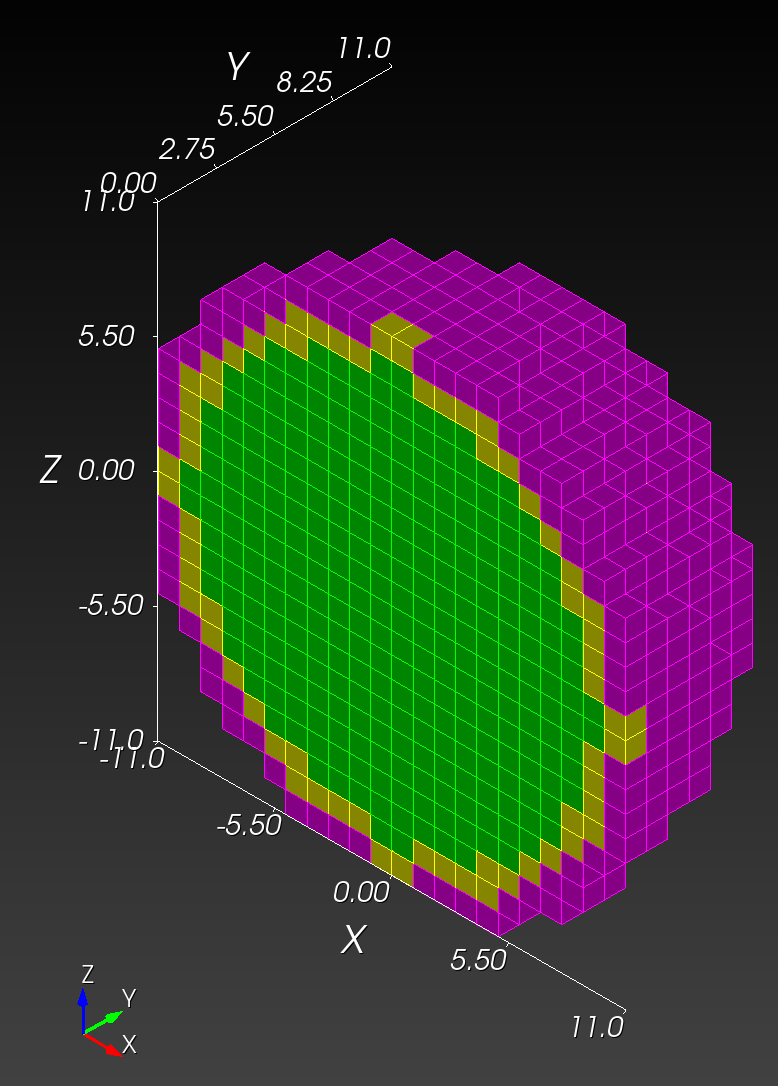 | 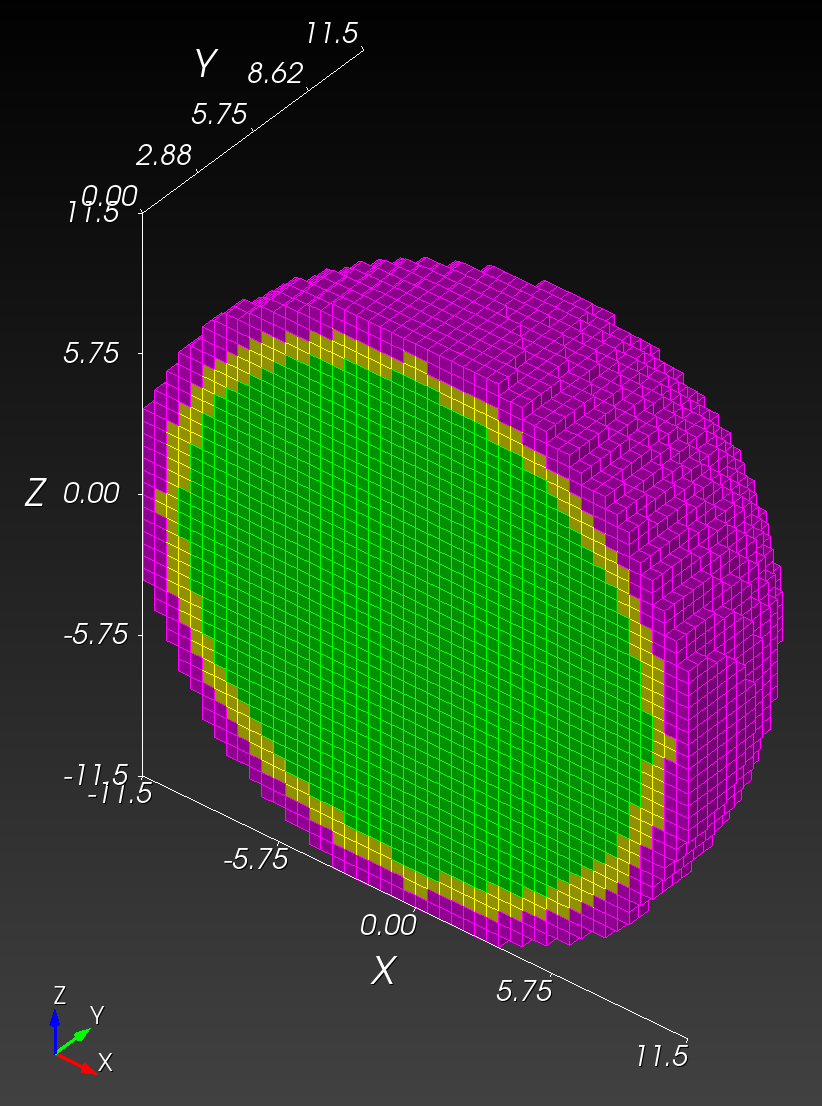 | 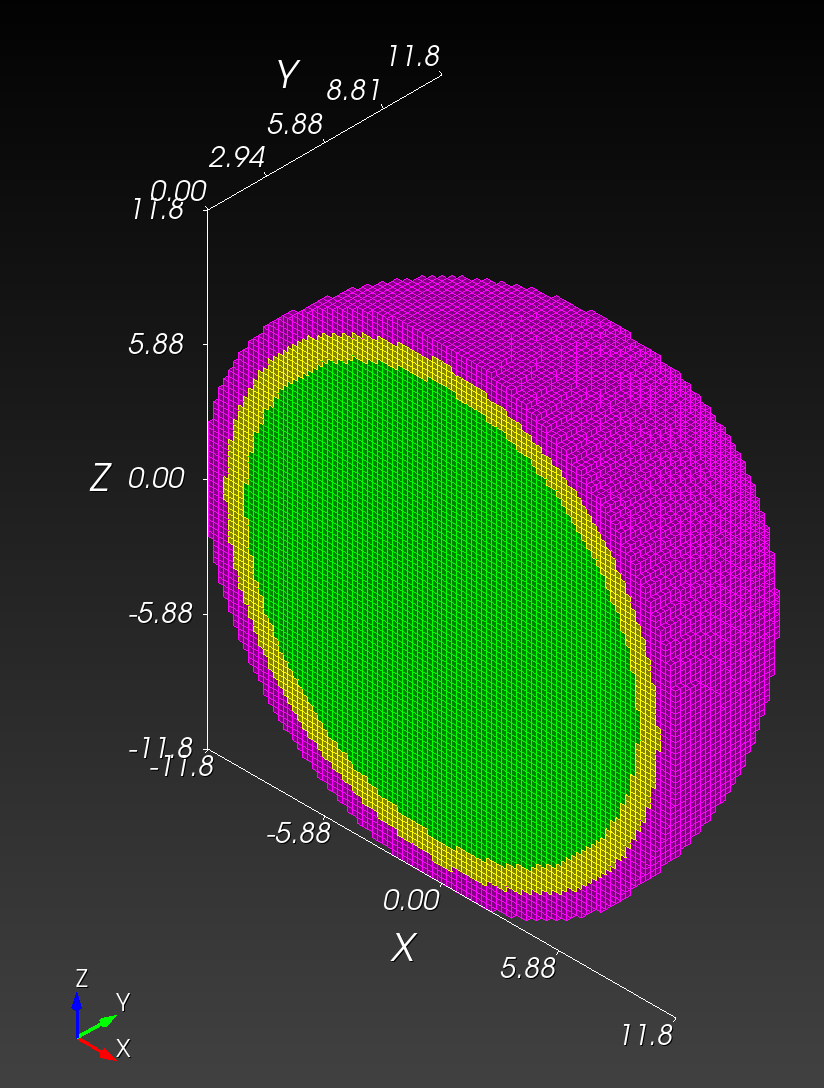 | 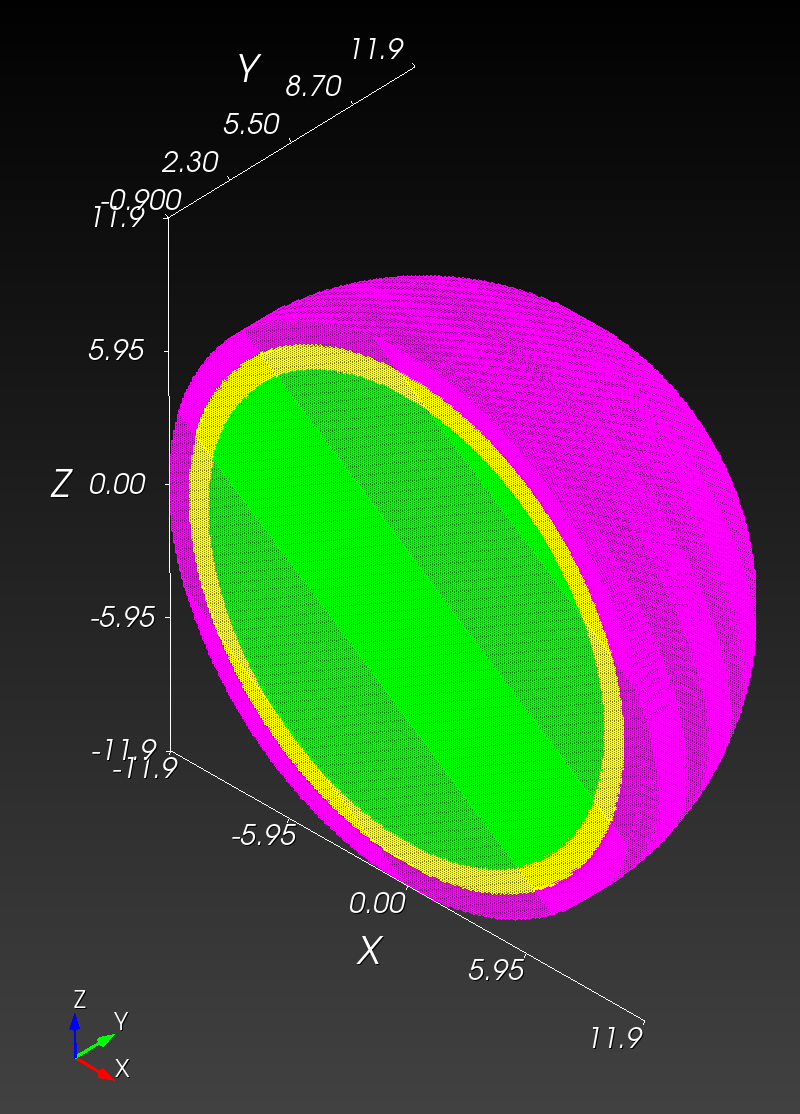 |
| block 1 (green) #elements | 3,648 | 31,408 | 259,408 | 4,136,832 |
| block 2 (yellow) #elements | 1,248 | 10,400 | 86,032 | 1,369,056 |
| block 3 (magenta) #elements | 1,376 | 12,280 | 103,240 | 1,639,992 |
| total #elements | 6,272 | 54,088 | 448,680 | 7,145,880 |
| Exodus file | spheres_resolution_1.exo (401 kB) | spheres_resolution_2.exo (3.2 MB) | spheres_resolution_3.exo (25.7 MB) | spheres_resolution_4.exo (404 MB) |
| Abaqus file | spheres_resolution_1.inp (962 kB) | spheres_resolution_2.inp (8.5 MB) | spheres_resolution_3.inp (73.6 MB) | spheres_resolution_4.inp (1.23 GB) |
Timing - Sculpt
Set up an alias, if needed.
alias sculpt='/Applications/Cubit-16.14/Cubit.app/Contents/MacOS/sculpt'
cd ~/autotwin/automesh/book/analysis/sphere_with_shells/
Use automesh to create .spn files from the .npy files.
automesh convert segmentation -i spheres_resolution_1.npy -o spheres_resolution_1.spn
automesh convert segmentation -i spheres_resolution_2.npy -o spheres_resolution_2.spn
automesh convert segmentation -i spheres_resolution_3.npy -o spheres_resolution_3.spn
automesh convert segmentation -i spheres_resolution_4.npy -o spheres_resolution_4.spn
Run Sculpt.
sculpt --num_procs 1 --input_spn "spheres_resolution_1.spn" \
-x 24 -y 24 -z 24 \
--xtranslate -24 --ytranslate -24 --ztranslate -24 \
--spn_xyz_order 0 \
--exodus_file "spheres_resolution_1" \
--stair 3
Total Time on 1 Procs 0.122201 sec. (0.002037 min.)
sculpt --num_procs 1 --input_spn "spheres_resolution_2.spn" \
-x 48 -y 48 -z 48 \
--xscale 0.5 --yscale 0.5 --zscale 0.5 \
--xtranslate -12 --ytranslate -12 --ztranslate -12 \
--spn_xyz_order 0 \
--exodus_file "spheres_resolution_2" \
--stair 3
Total Time on 1 Procs 0.792997 sec. (0.013217 min.)
sculpt --num_procs 1 --input_spn "spheres_resolution_3.spn" \
-x 96 -y 96 -z 96 \
--xscale 0.25 --yscale 0.25 --zscale 0.25 \
--xtranslate -12 --ytranslate -12 --ztranslate -12 \
--spn_xyz_order 0 \
--exodus_file "spheres_resolution_3" \
--stair 3
Total Time on 1 Procs 7.113380 sec. (0.118556 min.)
sculpt --num_procs 1 --input_spn "spheres_resolution_4.spn" \
-x 240 -y 240 -z 240 \
--xscale 0.1 --yscale 0.1 --zscale 0.1 \
--xtranslate -12 --ytranslate -12 --ztranslate -12 \
--spn_xyz_order 0 \
--exodus_file "spheres_resolution_4" \
--stair 3
Total Time on 1 Procs 135.636523 sec. (2.260609 min.)
The table below summarizes the relative processing times, Sculpt versus automesh (completed with automesh version 0.2.9)
| resolution | 1 vox/cm | 2 vox/cm | 4 vox/cm | 10 vox/cm |
|---|---|---|---|---|
automesh | 1 | 1 | 1 | 1 |
| Sculpt | 6.73 | 31.6 | 97.8 | 141 |
Simulation
Work in progress.
Meshes
Copy from local to HPC:
# for example, manual copy from local to HPC
# macOS local finder, command+K to launch "Connect to Server"
# smb://cee/chovey
# copy [local]~/autotwin/automesh/book/analysis/sphere_with_shells/spheres_resolution_2.exo
# to
# [HPC]~/autotwin/ssm/geometry/sr2/
We consider three simulations using the following three meshes (in the HPC ~/autotwin/ssm/geometry folder):
| folder | file | md5 checksum |
|---|---|---|
sr2 | spheres_resolution_2.exo | 9f40c8bd91874f87e22a456c76b4448c |
sr3 | spheres_resolution_3.exo | 6ae69132897577e526860515e53c9018 |
sr4 | spheres_resolution_4.exo | b939bc65ce07d3ac6a573a4f1178cfd0 |
We do not use the spheres_resolution_1.exo because the outer shell layer is not closed.
Boundary Conditions
Consider an angular acceleration pulse of the form:
and is zero otherwise. This pulse, referred to as the bump function, is continuously differentiable, with peak angular acceleration at .
With krad/s^2, and ms, we can create the angular acceleration boundary condition (with corresponding angular velocity) 1 plots:
| Angular Acceleration | Angular Velocity |
|---|---|
 |  |
Figure: Angular acceleration and corresponding angular velocity time history.
- Angular acceleration tabulated data: The standardized angular acceleration load curve has column data as (time, magnitude) in (sec, krad/s^2). The function used to generated the curve, from Equation (1) of 1, is
- Angular velocity tabulated data: The angular velocity curve has column data as (time, magnitude) in (sec, rad/s).
The peak angular acceleration ocurrs at (which occurs in the tabular data at data point 4144, values (0.00414310, 7.99999997)).
On the outer shell (block 3) of the model, we prescribe the angular velocity boundary condition.
Tracers
View the tracer locations in Cubit:
graphics clip on plane location 0 0 1 direction 0 0 -1
view up 0 1 0
view from 0 0 100
graphics clip manipulation off

Figure: Tracer numbers [0, 1, 2, ... 11] at distance [0, 1, 2, ... 11] centimeters from point (0, 0, 0) along the x-axis at resolutions sr2, sr3, and sr4 (top to bottom, respectively).
Materials
We model the outer shell (block 3) as a rigid body. The inner sphere (block 1) is nodeled as Swanson viscoelastic white matter. The intermediate material (block 2) is modeled as elastic cerebral spinal fluid.
Input deck
We created three input decks:
sr2.i(for meshspheres_reolution_2.exo)sr3.i(for meshspheres_reolution_3.exo)sr4.i(for meshspheres_reolution_4.exo)
Remark: Originally, we used APREPRO, part of SEACAS, to define tracer points along the line at 1-cm (radial) intervals. We then updated the locations of these tracer points to be along the x-axis, which allowed for nodally exact locations to be established across all models, voxelized and conforming.
Displacement, maximum principal log strain, and maximum principal rate of deformation were logged at tracer points over the simulation duration. The Sierra/Solid Mechanics documentation 2 3 was also useful for creating the input decks.
Solver
Request resources:
mywcid # see what wcid resources are available, gives an FYxxxxxx number
#request 1 interactive node for four hours with wcid account FY180100
salloc -N1 --time=4:00:00 --account=FY180100
See idle nodes:
sinfo
Decompose the geometry, e.g., ~/autotwin/ssm/geometry/sr2/submit_script:
#!/bin/bash
module purge
module load sierra
module load seacas
# previously ran with 16 processors
# PROCS=16
# 10 nodes = 160 processors
PROCS=160
# PROCS=320
# PROCS=336
# geometry and mesh file
GFILE="spheres_resolution_2.exo"
decomp --processors $PROCS $GFILE
Check the input deck ~/autotwin/ssm/input/sr2/sr2.i with submit_check:
#!/bin/bash
echo "This is submit_check"
echo "module purge"
module purge
echo "module load sierra"
module load sierra
# new, run this first
export PSM2_DEVICES='shm,self'
IFILE="sr2.i"
echo "Check syntax of input deck: $IFILE"
adagio --check-syntax -i $IFILE # to check syntax of input deck
# echo "Check syntax of input deck ($IFILE) and mesh loading"
adagio --check-input -i $IFILE # to check syntax of input deck and mesh load
Clean any preexisting result files with submit_clean:
#!/bin/bash
echo "This is submit_clean"
rm batch_*
rm sierra_batch_*
rm *.e.*
rm epu.log
rm *.g.*
rm *.err
rm g.rsout.*
Submit the job with submit_script:
#!/bin/bash
echo "This is submit_script"
module purge
module load sierra
module load seacas
# PROCS=16
PROCS=160
# PROCS=320
# PROCS=336
# geometry and mesh file
# GFILE="../../geometry/sphere/spheres_resolution_4.exo"
# decomp --processors $PROCS $GFILE
IFILE="sr2.i"
# queues
# https://wiki.sandia.gov/pages/viewpage.action?pageId=1359570410#SlurmDocumentation-Queues
# short can be used for nodes <= 40 and wall time <= 4:00:00 (4 hours)
# batch, the default queue, wall time <= 48 h
# long, wall time <= 96 h, eclipse 256 nodes
# https://wiki.sandia.gov/display/OK/Slurm+Documentation
# over 4 hours, then need to remove 'short' from the --queue-name
#
# sierra -T 00:20:00 --queue-name batch,short --account FY180042 -j $PROCS --job-name $IFILE --run adagio -i $IFILE
sierra -T 04:00:00 --queue-name batch,short --account FY180042 -j $PROCS --job-name $IFILE --run adagio -i $IFILE
# sierra -T 06:00:00 --queue-name batch --account FY180042 -j $PROCS --job-name $IFILE --run adagio -i $IFILE
# sierra -T 24:00:00 --queue-name batch --account FY180042 -j $PROCS --job-name $IFILE --run adagio -i $IFILE
Monitor the job:
# monitoring
squeue -u chovey
tail foo.log
tail -f foo.log # interactive monitor
Add shortcuts, if desired, to the ~/.bash_profile:
alias sq="squeue -u chovey"
alias ss="squeue -u chovey --start"
Cancel the job:
scancel JOB_ID
scancel -u chovey # cancel all jobs
Compute time:
| item | sim | T_sim (ms) | HPC | #proc | cpu time (hh:mm) |
|---|---|---|---|---|---|
| 0 | sr2.i | 20 | att | 160 | less than 1 min |
| 1 | sr3.i | 20 | att | 160 | 00:04 |
| 2 | sr4.i | 20 | ecl | 160 | 03:58 |
Results
Copy the files, history_rigid.csv and history.csv, which contain tracer rigid and deformable body time histories, from the HPC to the local.
Rigid Body
With figio and the rigid_body_ang_kinematics.yml recipe,
cd ~/autotwin/automesh/book/analysis/sphere_with_shells/recipes
figio rigid_body_ang_kinematics.yml
verify that the rigid body input values were sucessfully reflected in the output:
| angular acceleration | angular velocity | angular position |
|---|---|---|
 |  |  |
Figure: Rigid body (block 3) kinematics for sr2, the sphere_resolution_2.exo model. The time history traces appear the same for the sr3 and sr4 models.
Deformable Body
The following figure shows the maximum principal log strain for various resolutions and selected times.
| resolution | 2 vox/cm | 4 vox/cm | 10 vox/cm |
|---|---|---|---|
| midline |  |  |  |
| t=0.000 s | 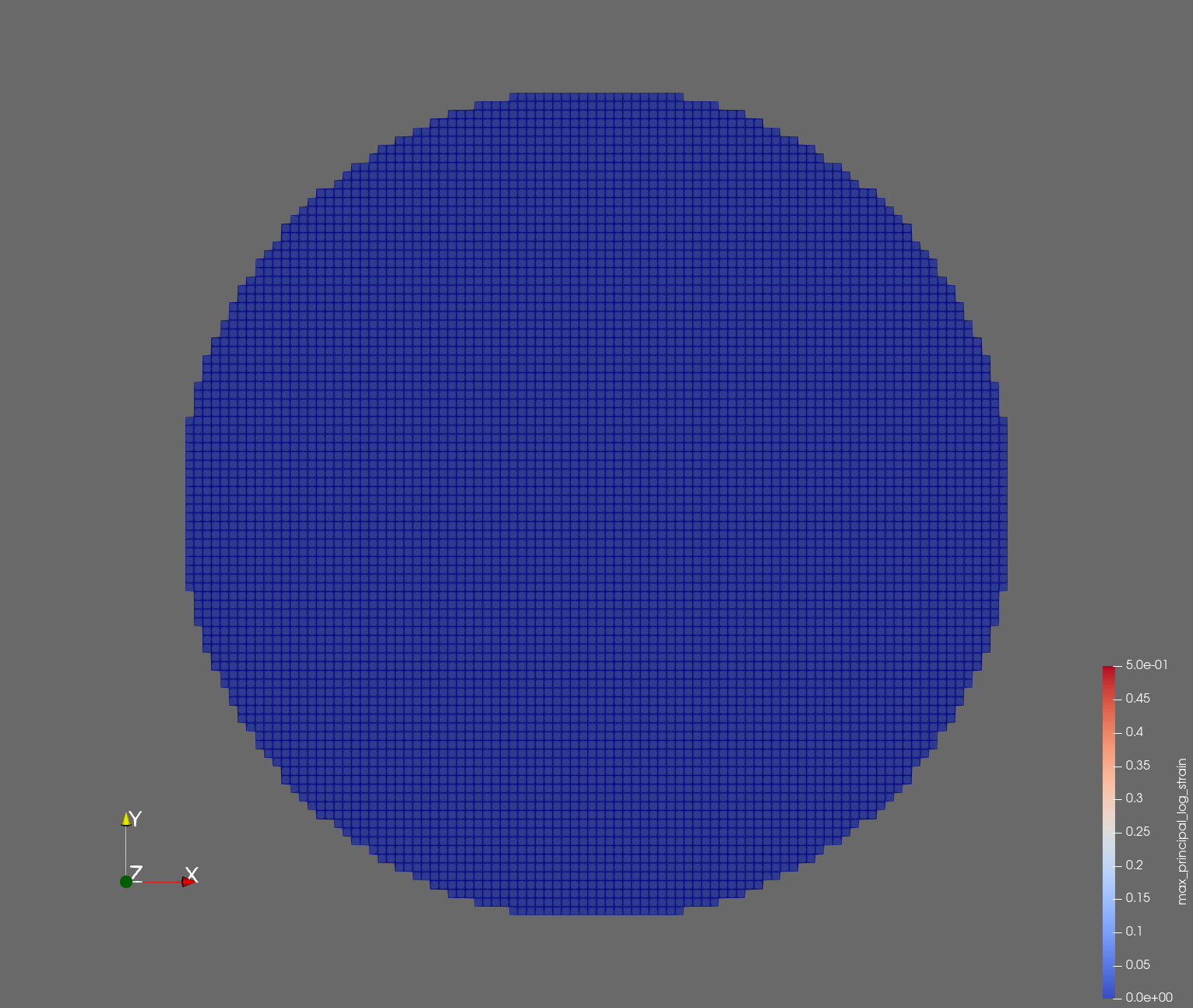 |  |  |
| t=0.002 s |  |  |  |
| t=0.004 s |  |  |  |
| t=0.006 s |  |  |  |
| t=0.008 s |  | 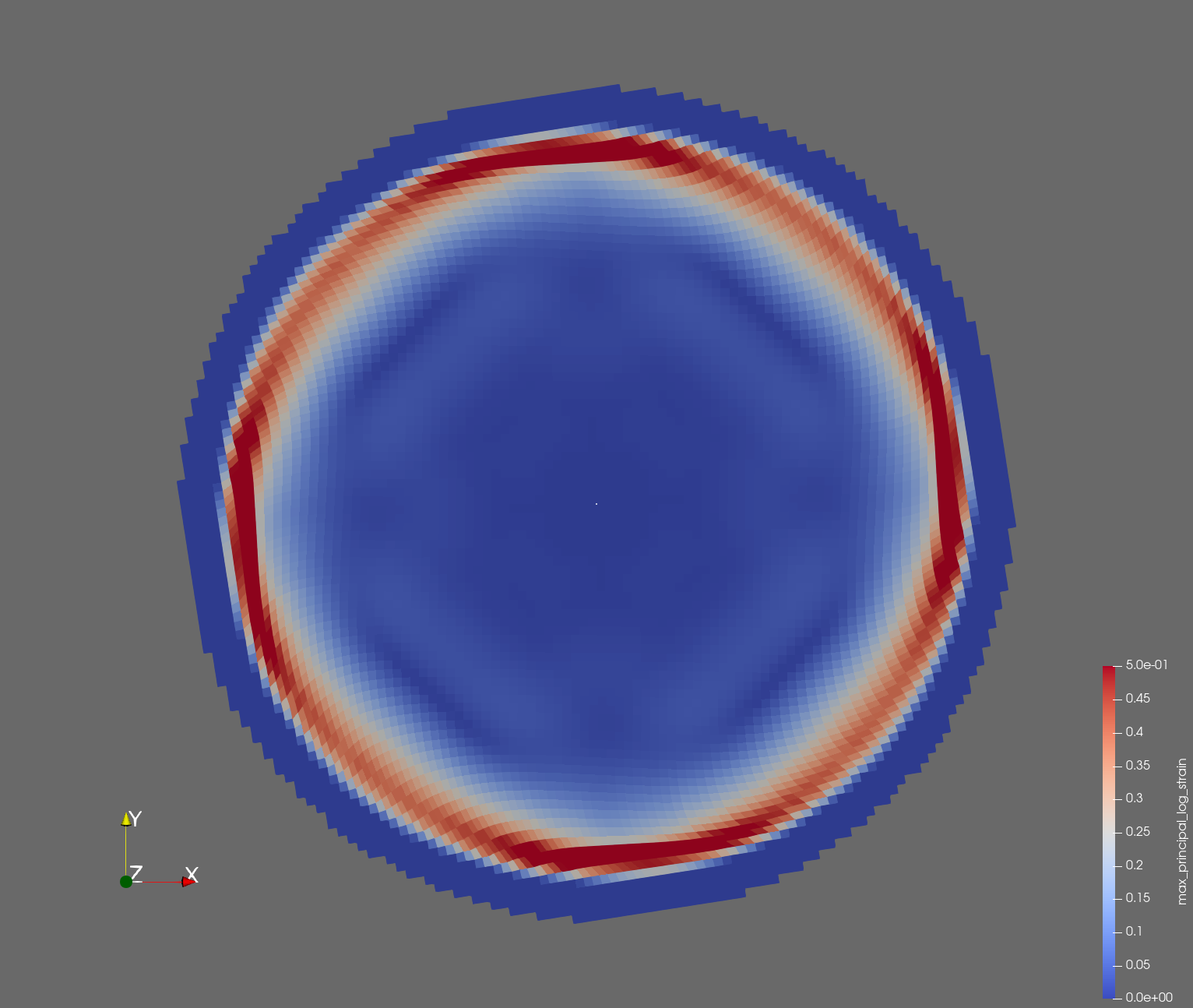 |  |
| t=0.010 s |  | 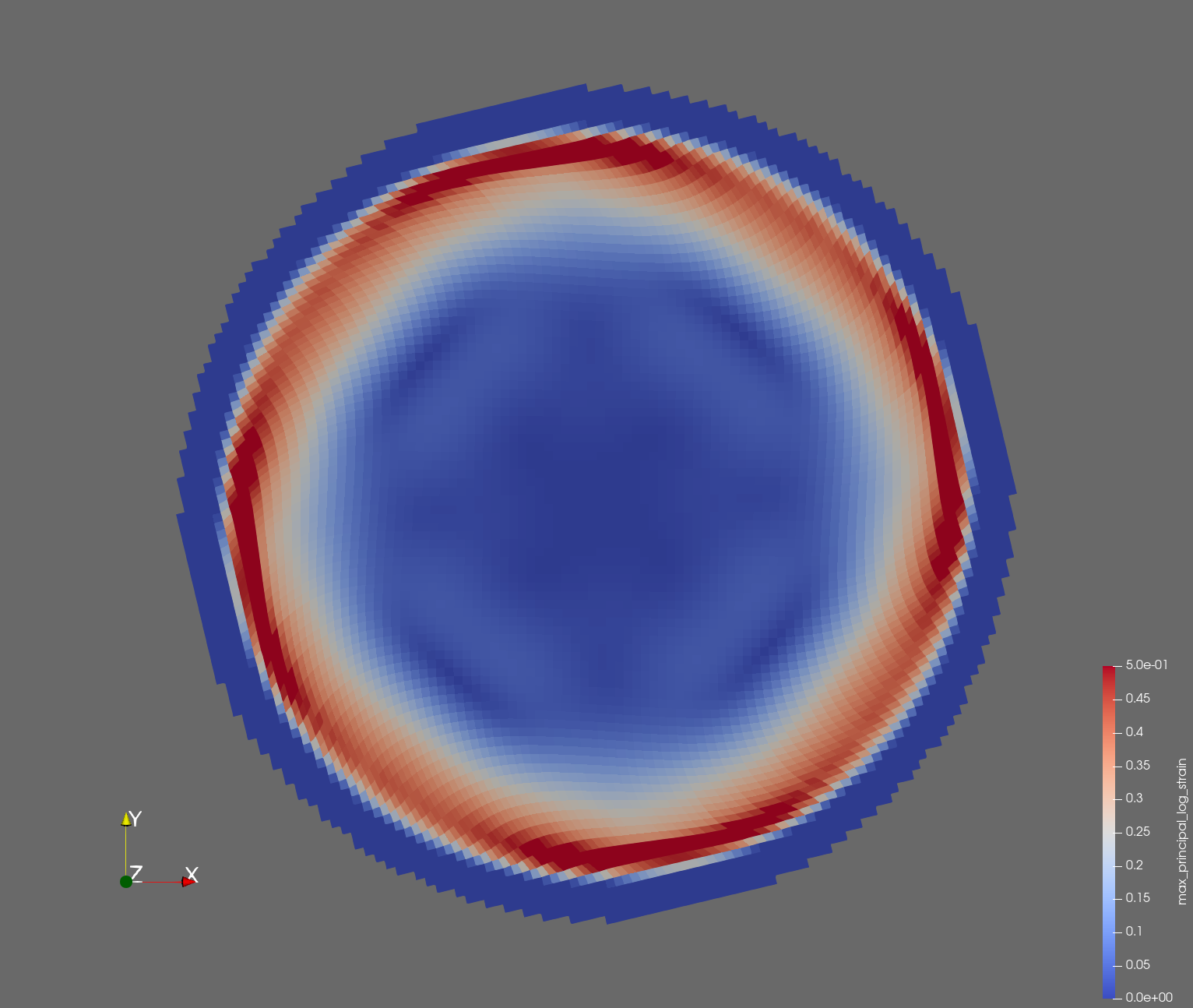 |  |
| t=0.012 s | 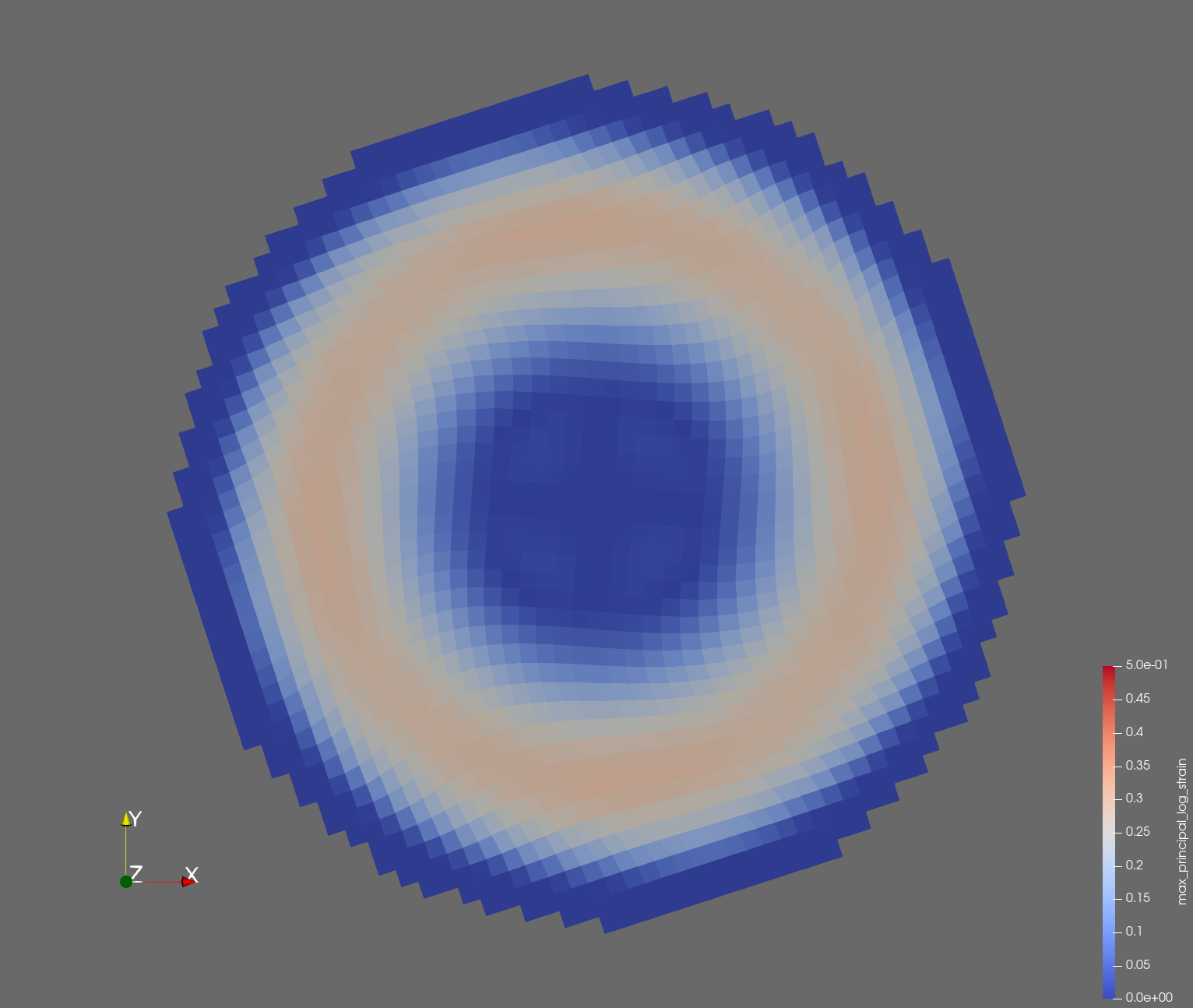 | 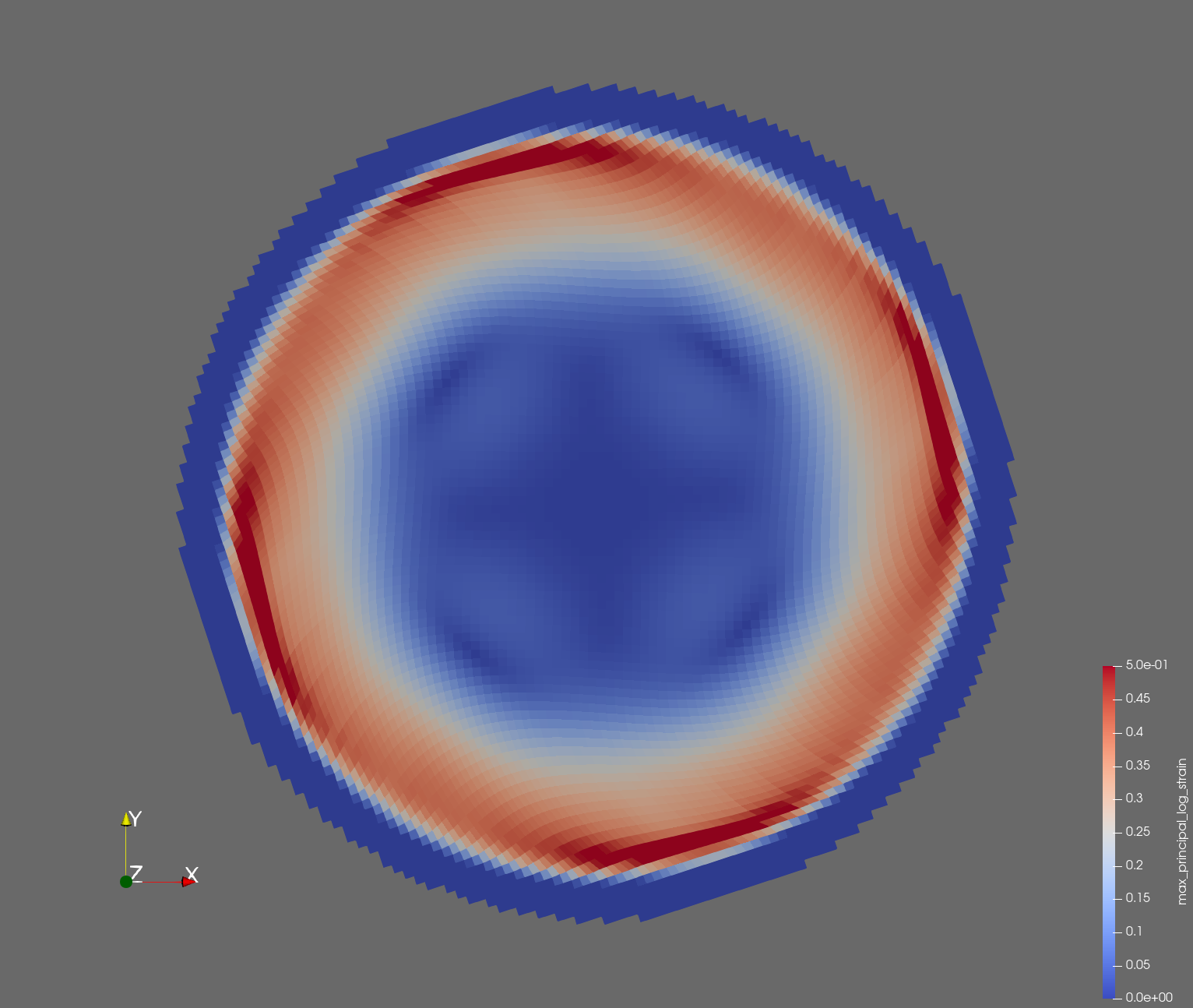 |  |
| t=0.014 s | 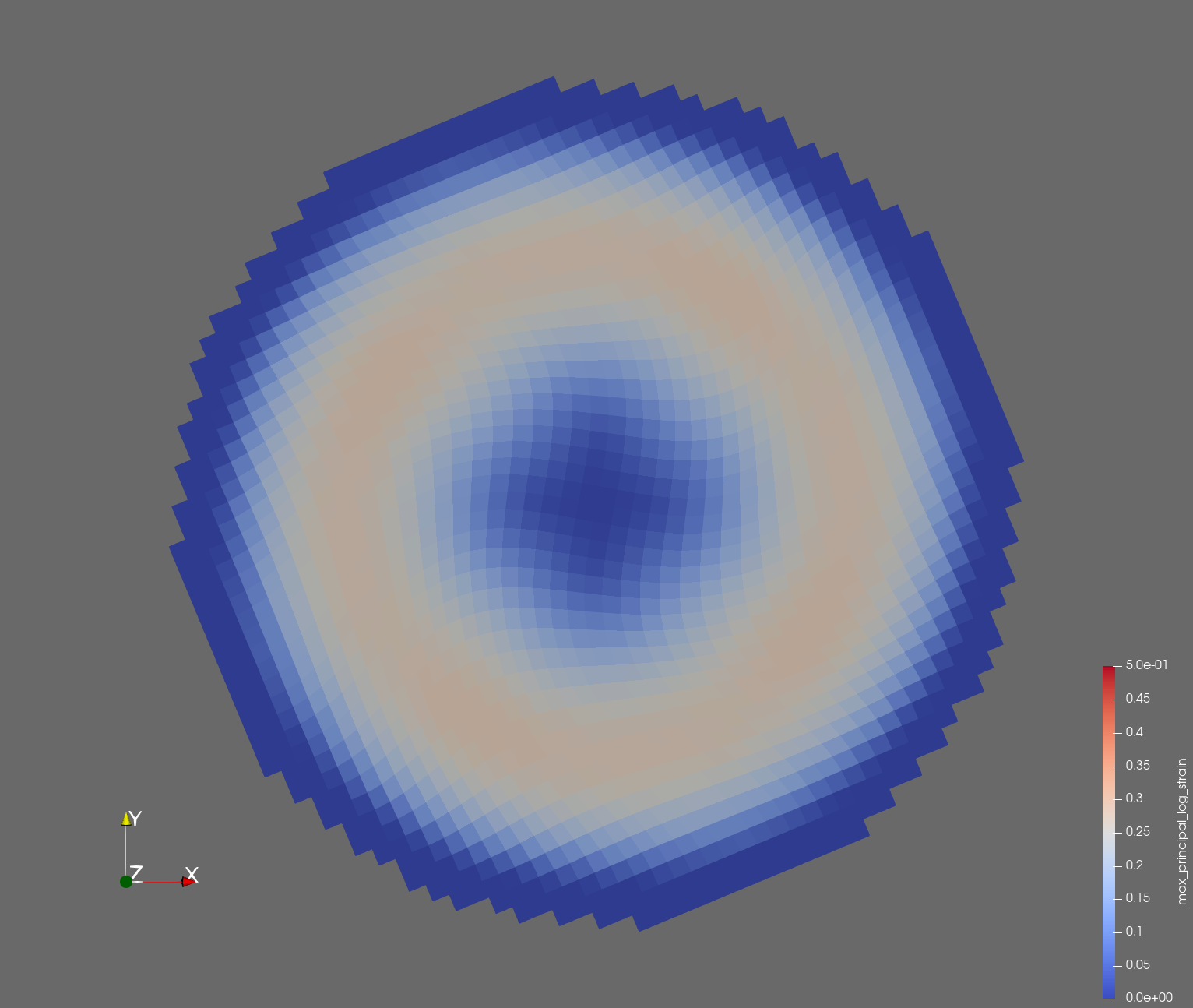 | 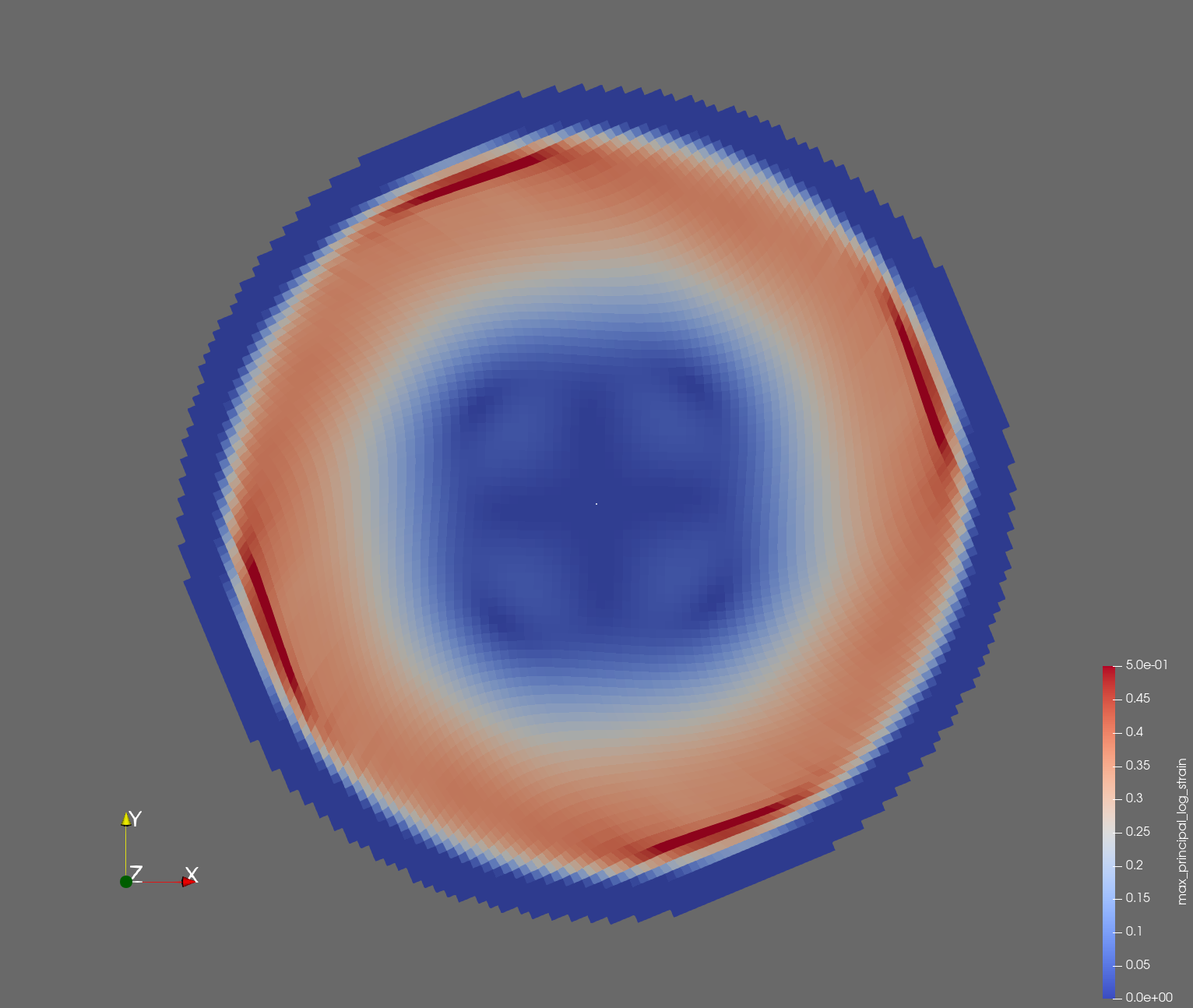 |  |
| t=0.016 s | 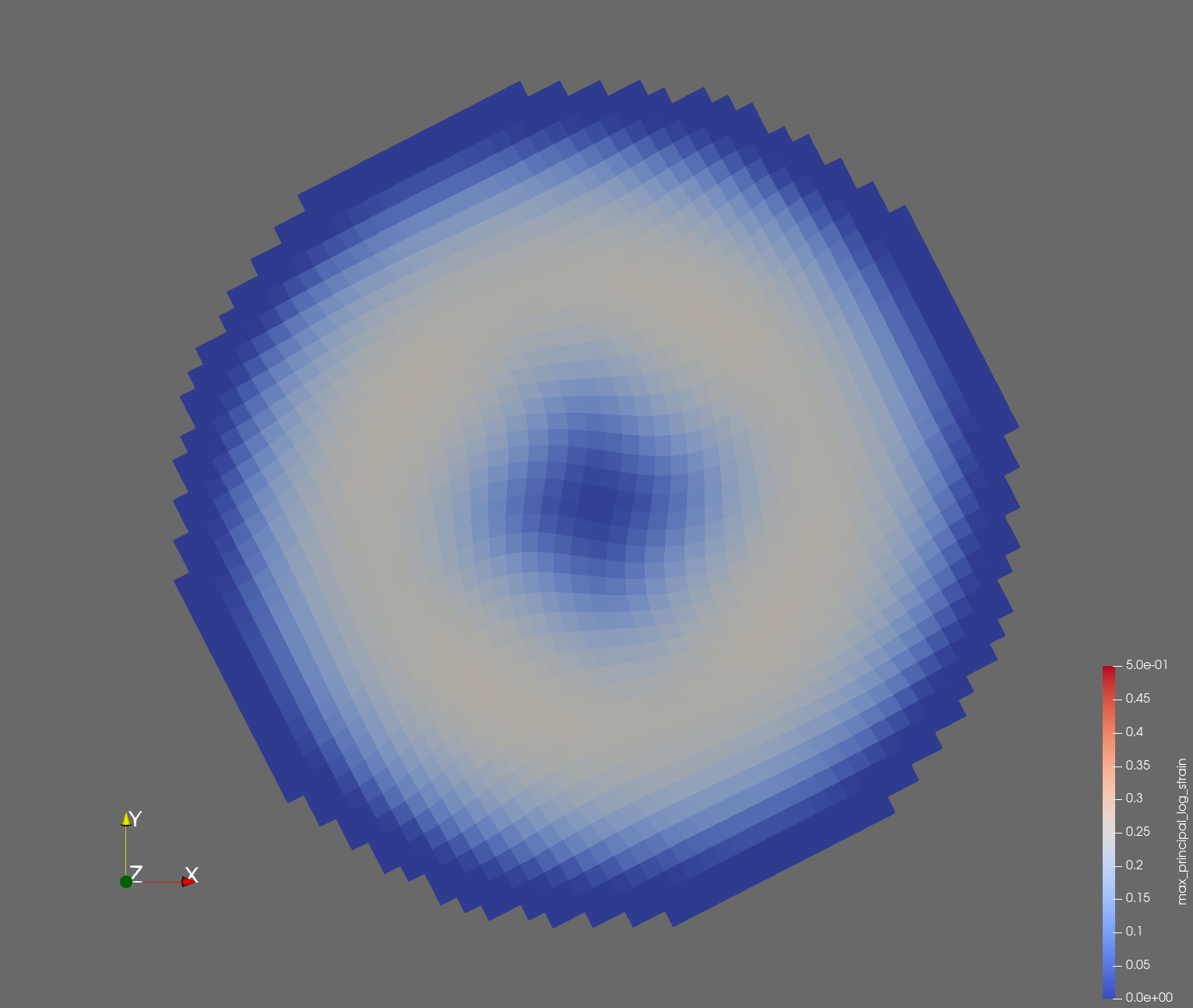 | 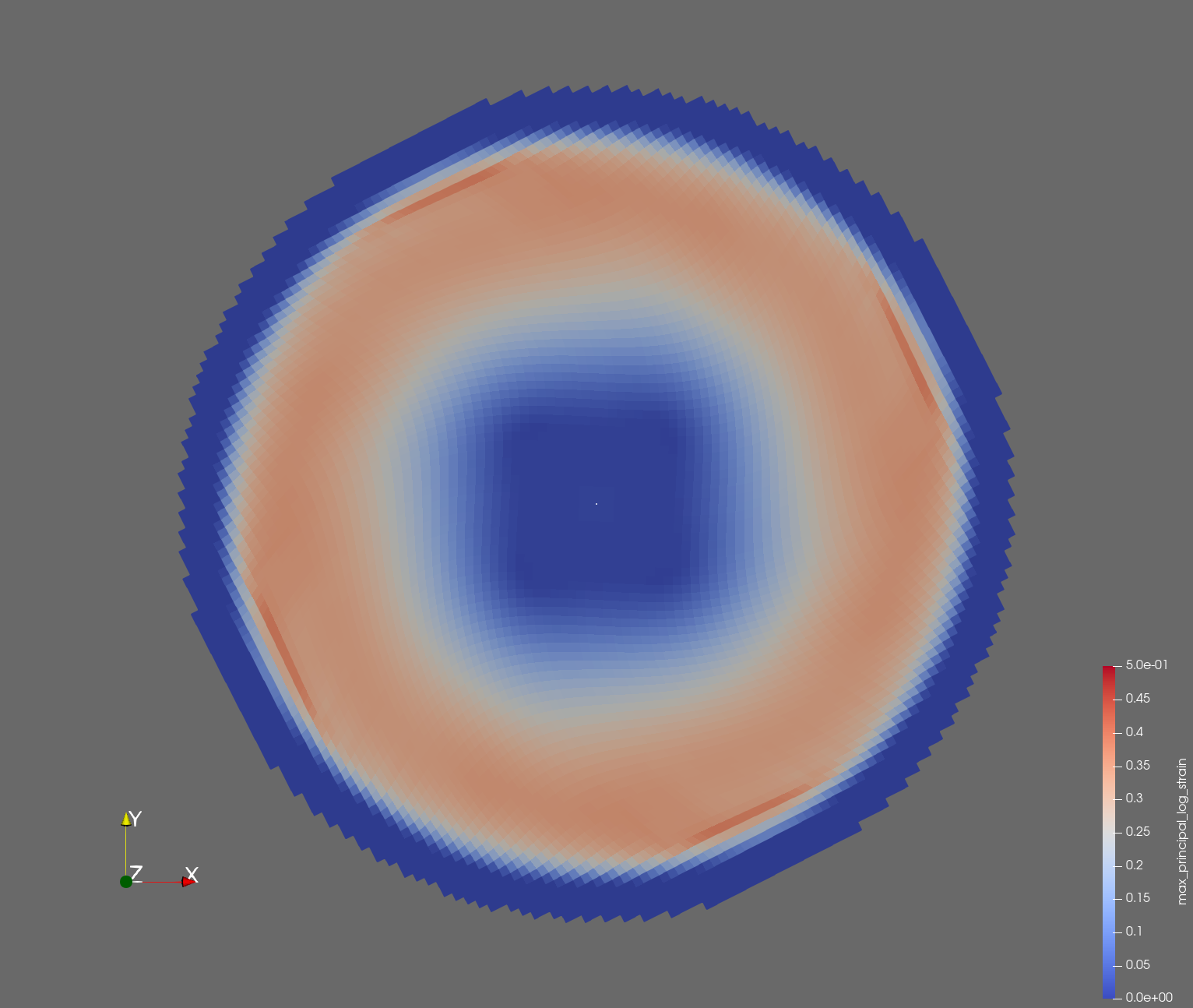 |  |
| t=0.018 s | 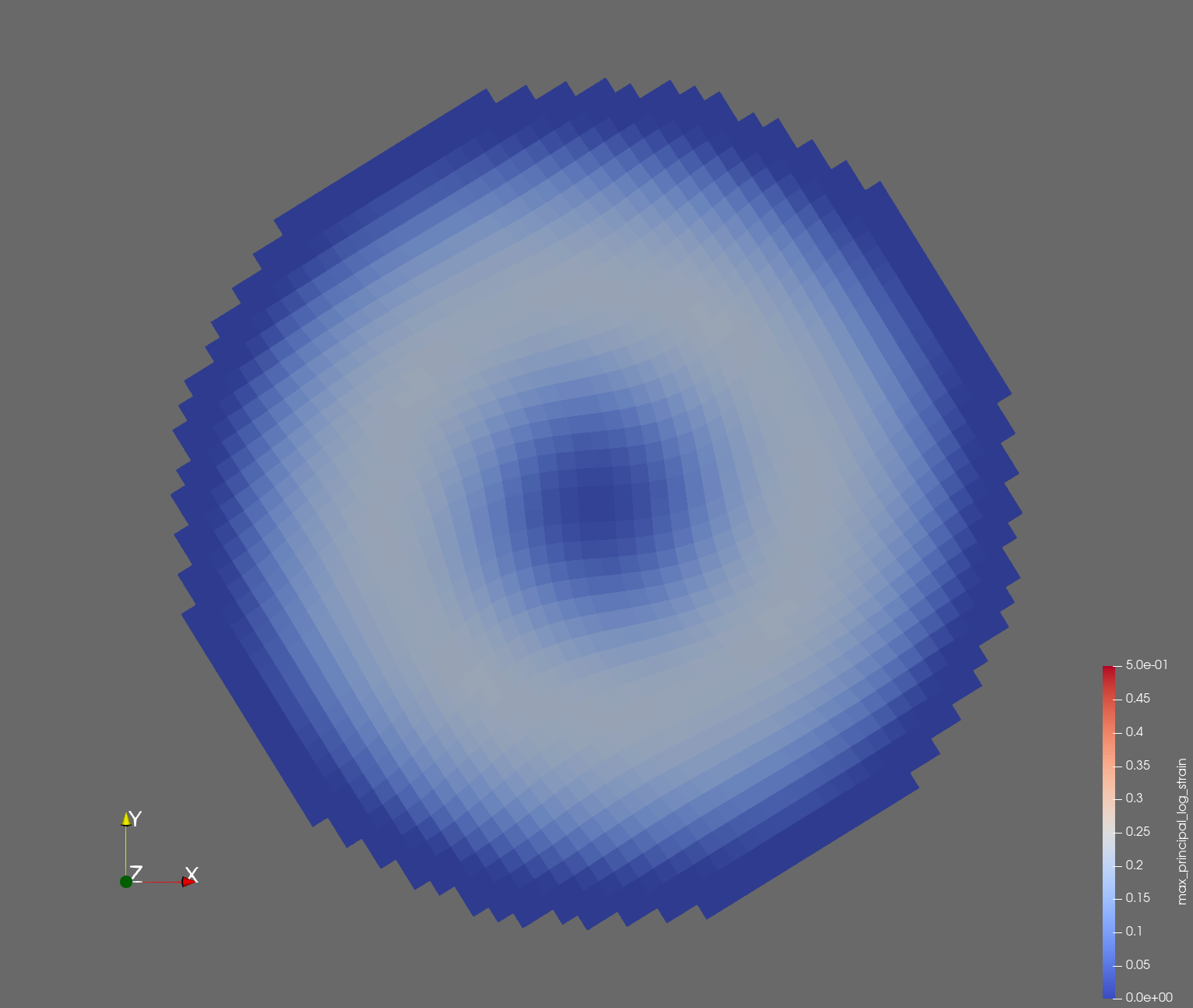 | 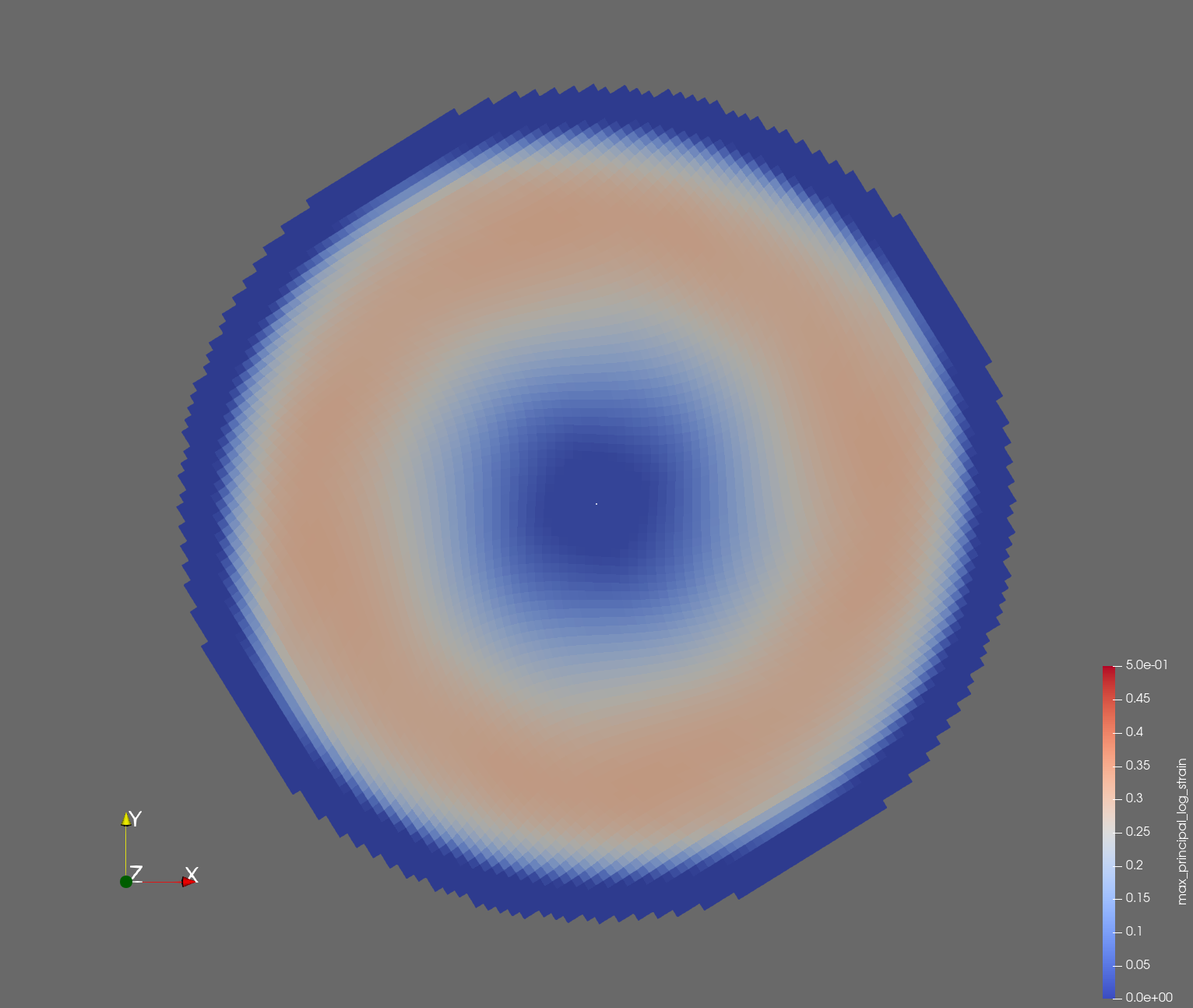 |  |
| t=0.020 s |  |  |  |
| displacement |  |  |  |
| recipe | displacement_sr2.yml | displacement_sr3.yml | displacement_sr4.yml |
| log strain |  |  |  |
| recipe | log_strain_sr2.yml | log_strain_sr3.yml | log_strain_sr4.yml |
| rate of deformation |  |  |  |
| recipe | rate_of_deformation_sr2.yml | rate_of_deformation_sr3.yml | rate_of_deformation_sr4.yml |
Figure: Voxel mesh midline section, with contour plot of maximum principal log strain at selected times from 0.000 s to 0.020 s (1,000 Hz sample rate, = 0.001 s), and tracer plots at 1 cm interval along the -axis for displacement magnitude, log strain, and rate of deformation (4,000 Hz acquisition rate, = 0.00025 s).
References
-
Carlsen RW, Fawzi AL, Wan Y, Kesari H, Franck C. A quantitative relationship between rotational head kinematics and brain tissue strain from a 2-D parametric finite element analysis. Brain Multiphysics. 2021 Jan 1;2:100024. paper ↩ ↩2
-
Beckwith FN, Bergel GL, de Frias GJ, Manktelow KL, Merewether MT, Miller ST, Parmar KJ, Shelton TR, Thomas JD, Trageser J, Treweek BC. Sierra/SolidMechanics 5.10 Theory Manual. Sandia National Lab. (SNL-NM), Albuquerque, NM (United States); Sandia National Lab. (SNL-CA), Livermore, CA (United States); 2022 Sep 1. link ↩
-
Thomas JD, Beckwith F, Buche MR, de Frias GJ, Gampert SO, Manktelow K, Merewether MT, Miller ST, Mosby MD, Parmar KJ, Rand MG, Schlinkman RT, Shelton TR, Trageser J, Treweek B, Veilleux MG, Wagman EB. Sierra/SolidMechanics 5.22 Example Problems Manual. Sandia National Lab. (SNL-NM), Albuquerque, NM (United States); Sandia National Lab. (SNL-CA), Livermore, CA (United States); 2024 Oct 1. link ↩
Conforming Mesh
In this section, we develop a traditional conforming mesh, manually constructed with Cubit. We compare the results from the conforming resolutions to the results obtained from the voxel mesh resolutions.
Mesh Creation and Visualization
With conforming_spheres.jou in Cubit, we create three conforming meshes to match the three voxel meshes of resolution 0.5, 0.25, and 0.1 cm (2 vox/cm, 4 vox/cm, and 10 vox/cm, respectively).
| resolution | 2 vox/cm | 4 vox/cm | 10 vox/cm |
|---|---|---|---|
| midline | 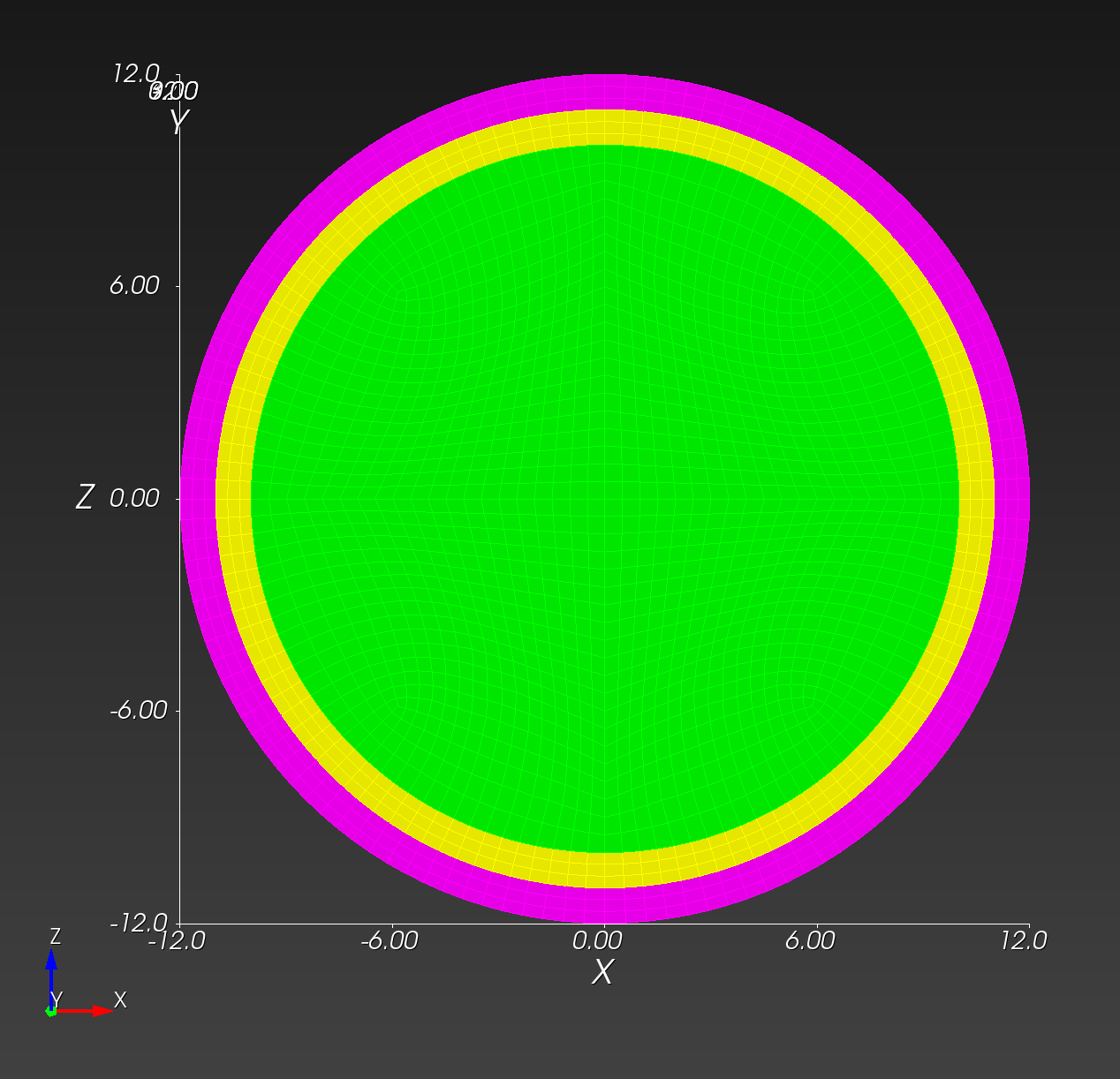 | 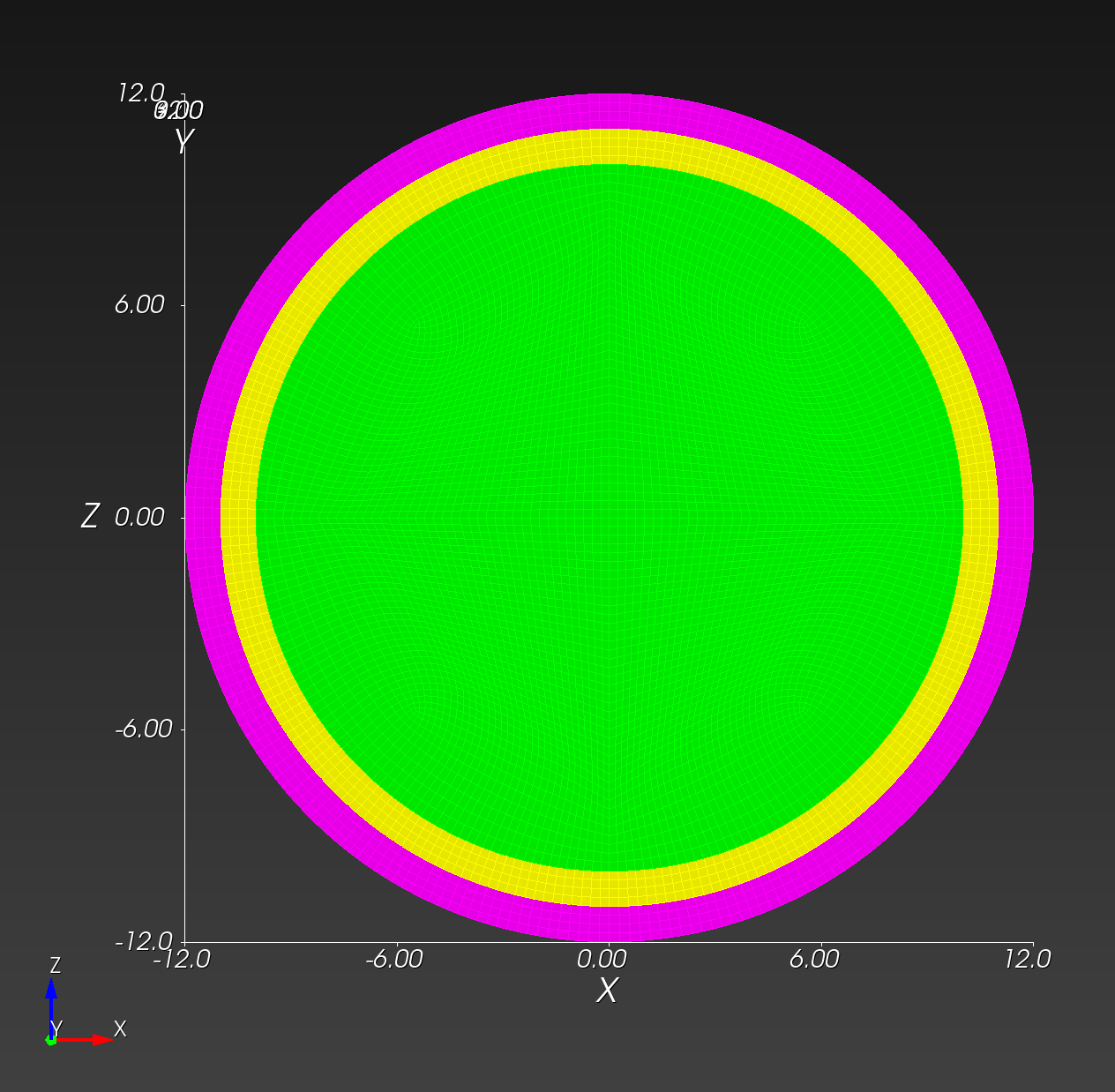 | 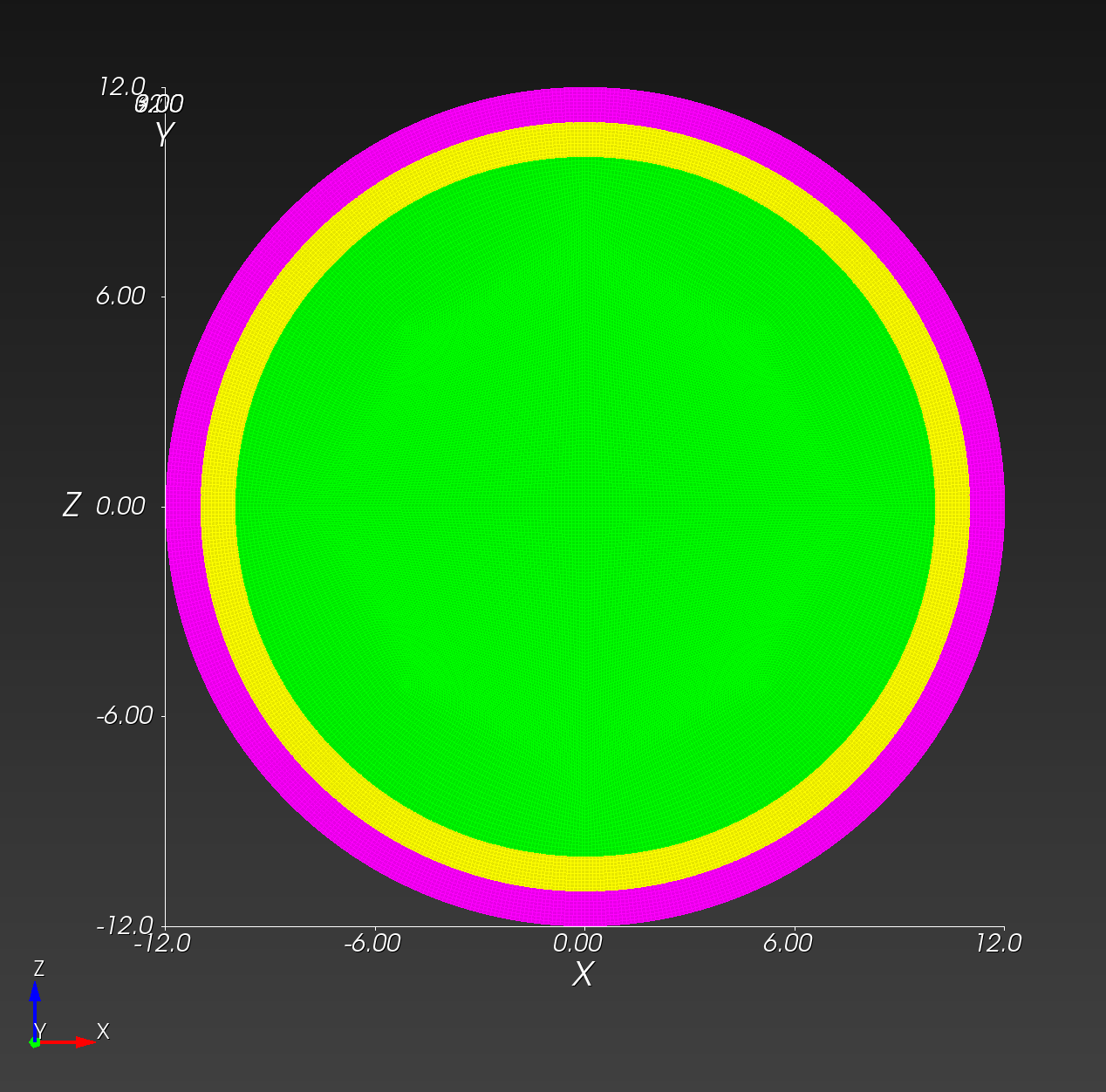 |
| isometric | 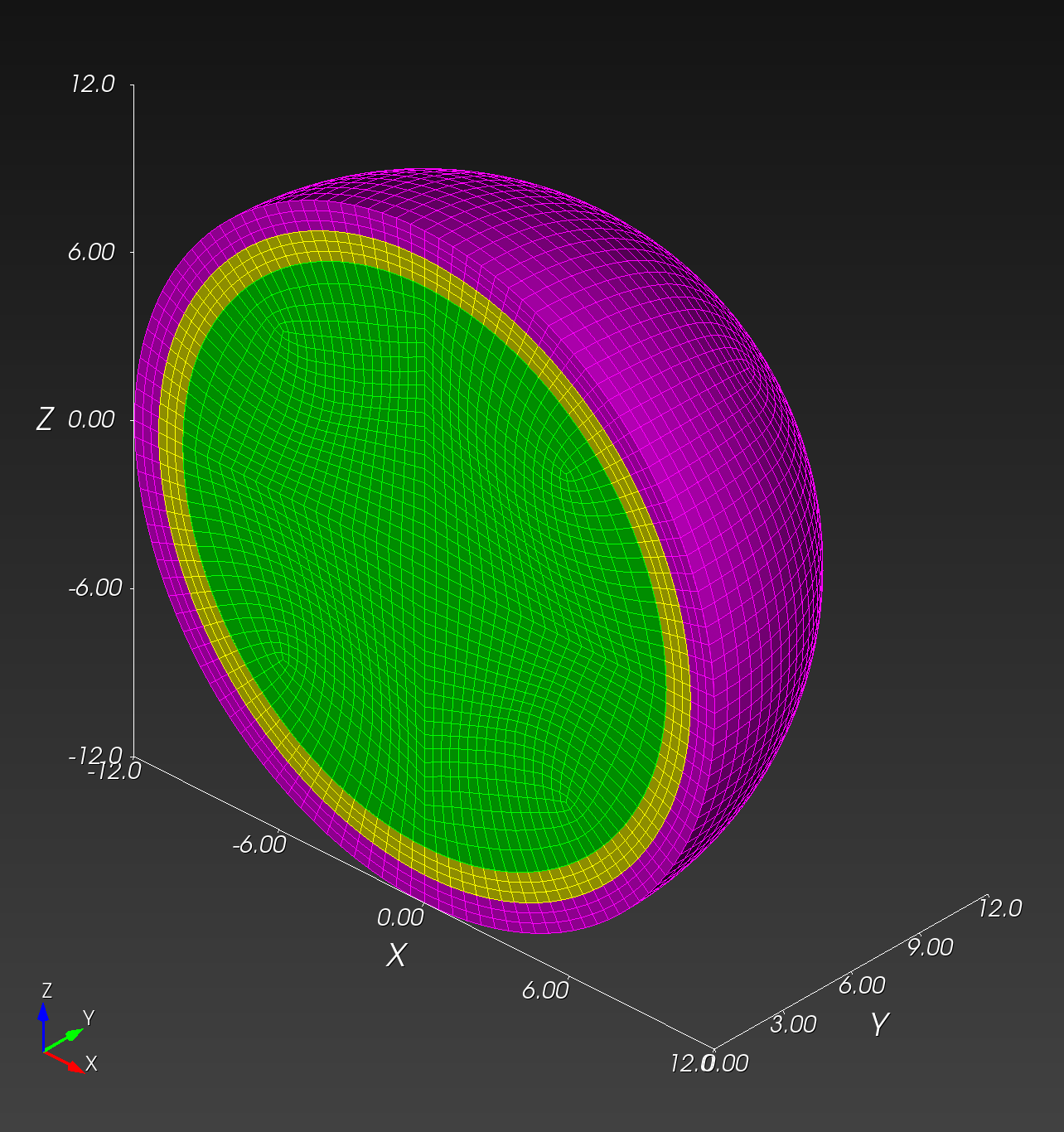 | 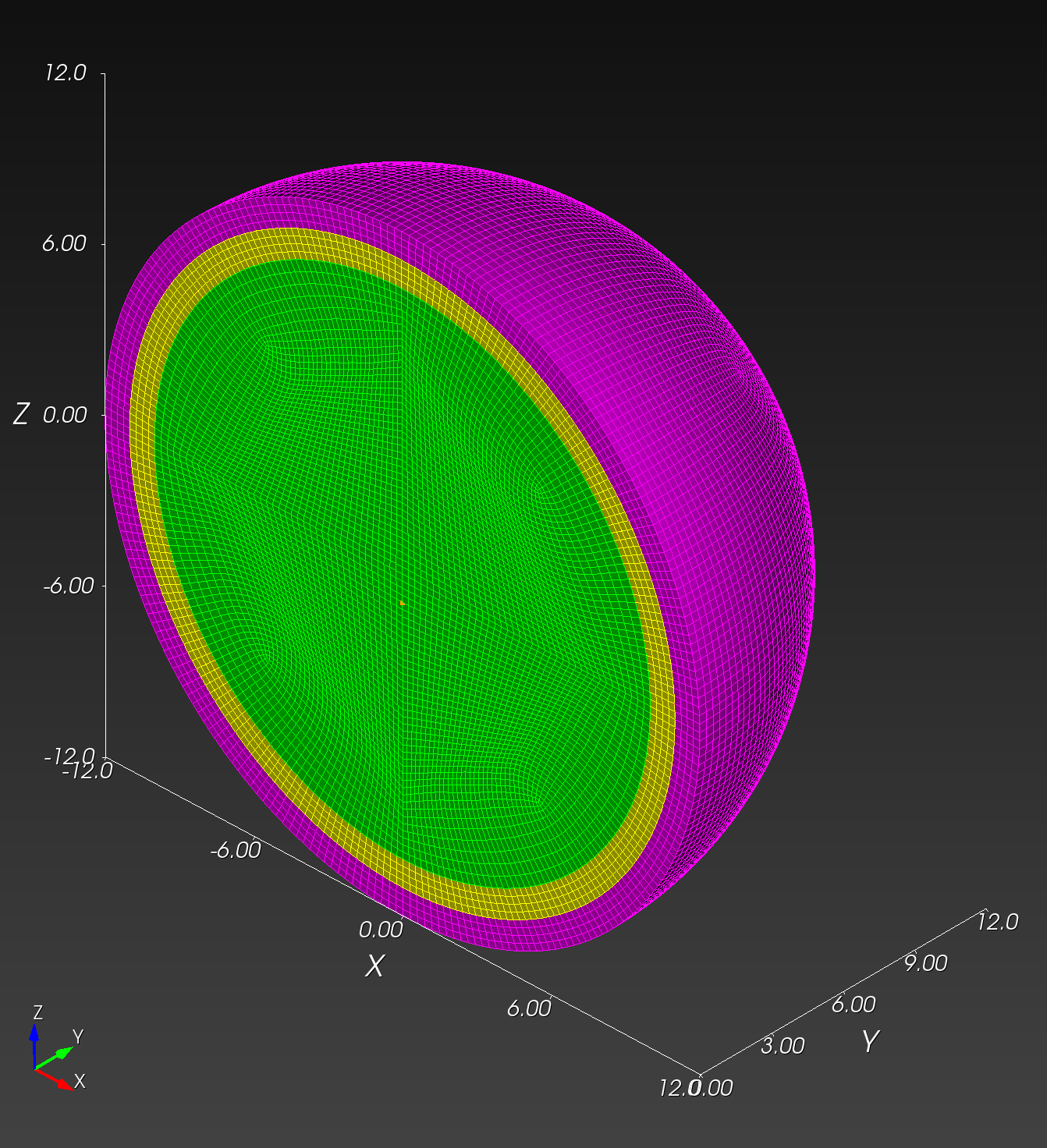 | 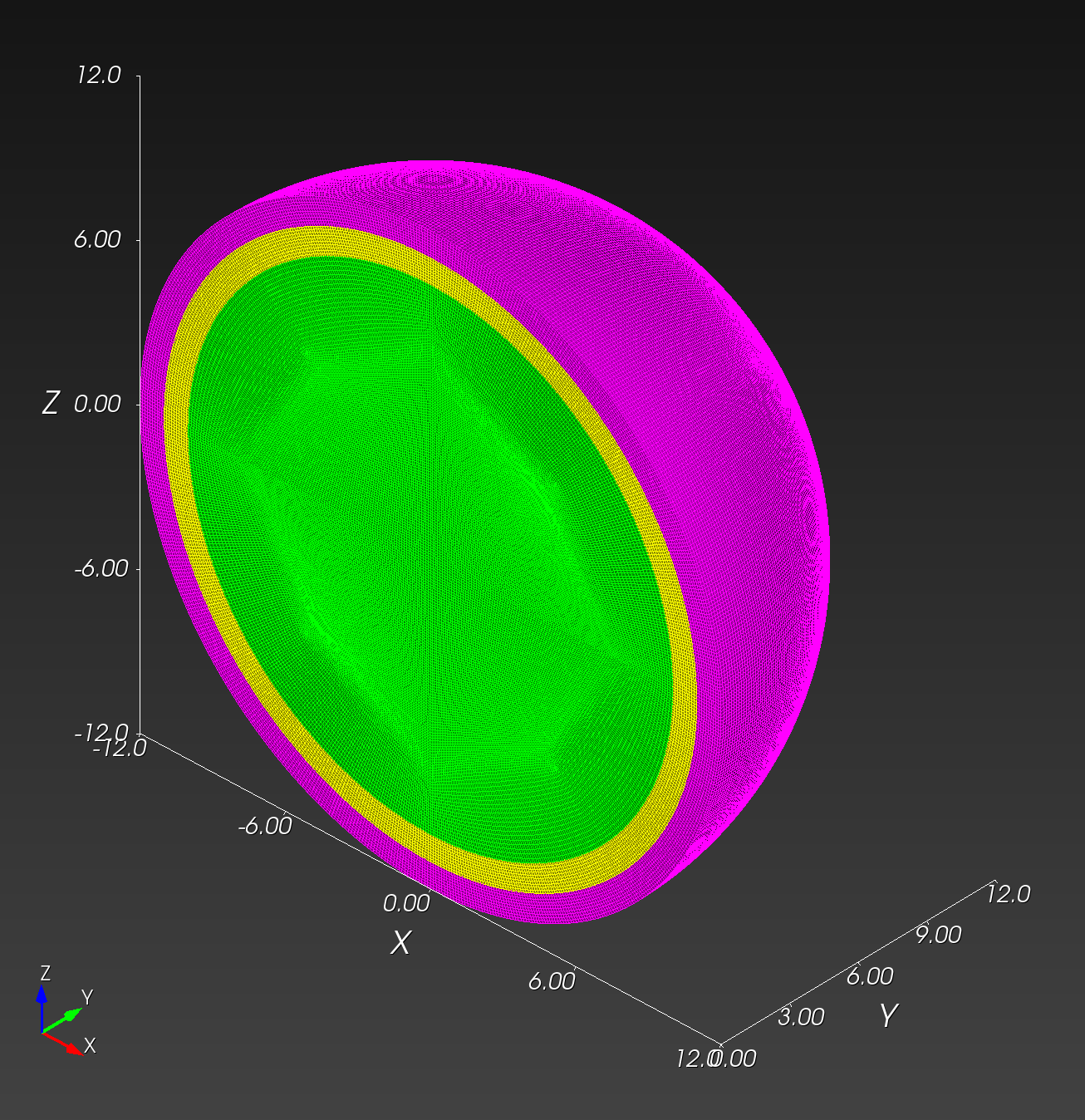 |
| block 1 (green) #elements | 57,344 | 458,752 | 7,089,776 |
| block 2 (yellow) #elements | 18,432 | 98,304 | 1,497,840 |
| block 3 (magenta) #elements | 18,432 | 98,304 | 1,497,840 |
| total #elements | 94,208 | 655,360 | 10,085,456 |
Copy from local to HPC:
# for example, manual copy from local to HPC
# macOS local finder, command+K to launch "Connect to Server"
# smb://cee/chovey
# copy [local]~/autotwin/automesh/book/analysis/sphere_with_shells/conf_0.5cm.g
# to
# [HPC]~/autotwin/ssm/geometry/sr2c/
We consider three simulations using the following three meshes (in the HPC ~/autotwin/ssm/geometry folder or downloadable from the links in the file column below):
| folder | file | md5 checksum | size |
|---|---|---|---|
sr2c | conf_0.5cm.g | 3731460f73da70ae79dd8155e2a8e0c6 | 7 MB |
sr3c | conf_0.25cm.g | bf65e329f43867c8fabc64b1b5273b8c | 47 MB |
sr4c | conf_0.1cm.g | ae0b13dec173c8fb030feab306a09db6 | 700 MB |
Tracers
View the tracer locations in Cubit:
graphics clip on plane location 0 0 1 direction 0 0 -1
view up 0 1 0
view from 0 0 100
graphics clip manipulation off

Figure: Tracer numbers [0, 1, 2, ... 11] at distance [0, 1, 2, ... 11] centimeters from point (0, 0, 0) along the x-axis at resolutions sr2c, sr3c, and sr4c (top to bottom, respectively).
Simulation
We created three input decks:
Results
Compute time:
| item | sim | T_sim (ms) | HPC | #proc | cpu time (hh:mm) |
|---|---|---|---|---|---|
| 0 | sr2c.i | 20 | gho | 160 | 00:02 |
| 1 | sr3c.i | 20 | gho | 160 | 00:21 |
| 2 | sr4.i | 20 | att | 160 | 14:00 (est) |
Rigid Body
We verified the rigid body kinematics match those from the voxel mesh, but we don't repeat those time history plots here.
Deformable Body
| resolution | 2 vox/cm | 4 vox/cm | 10 vox/cm |
|---|---|---|---|
| midline |  |  |  |
| displacement |  |  |  |
| recipe | displacement_sr2c.yml | displacement_sr3c.yml | displacement_sr4c.yml |
| log strain |  |  |  |
| recipe | log_strain_sr2c.yml | log_strain_sr3c.yml | log_strain_sr4c.yml |
| rate of deformation |  |  |  |
| recipe | rate_of_deformation_sr2c.yml | rate_of_deformation_sr3c.yml | rate_of_deformation_sr4c.yml |
Figure: Conforming mesh midline section and tracer plots at 1 cm interval along the -axis for displacement magnitude, log strain, and rate of deformation (10,000 Hz acquisition rate, = 0.0001 s).
Smoothed Mesh
alias automesh='~/autotwin/automesh/target/release/automesh'
cd ~/autotwin/automesh/book/analysis/sphere_with_shells
Taubin Smoothing
sr2s10 | sr2s50 |
|---|---|
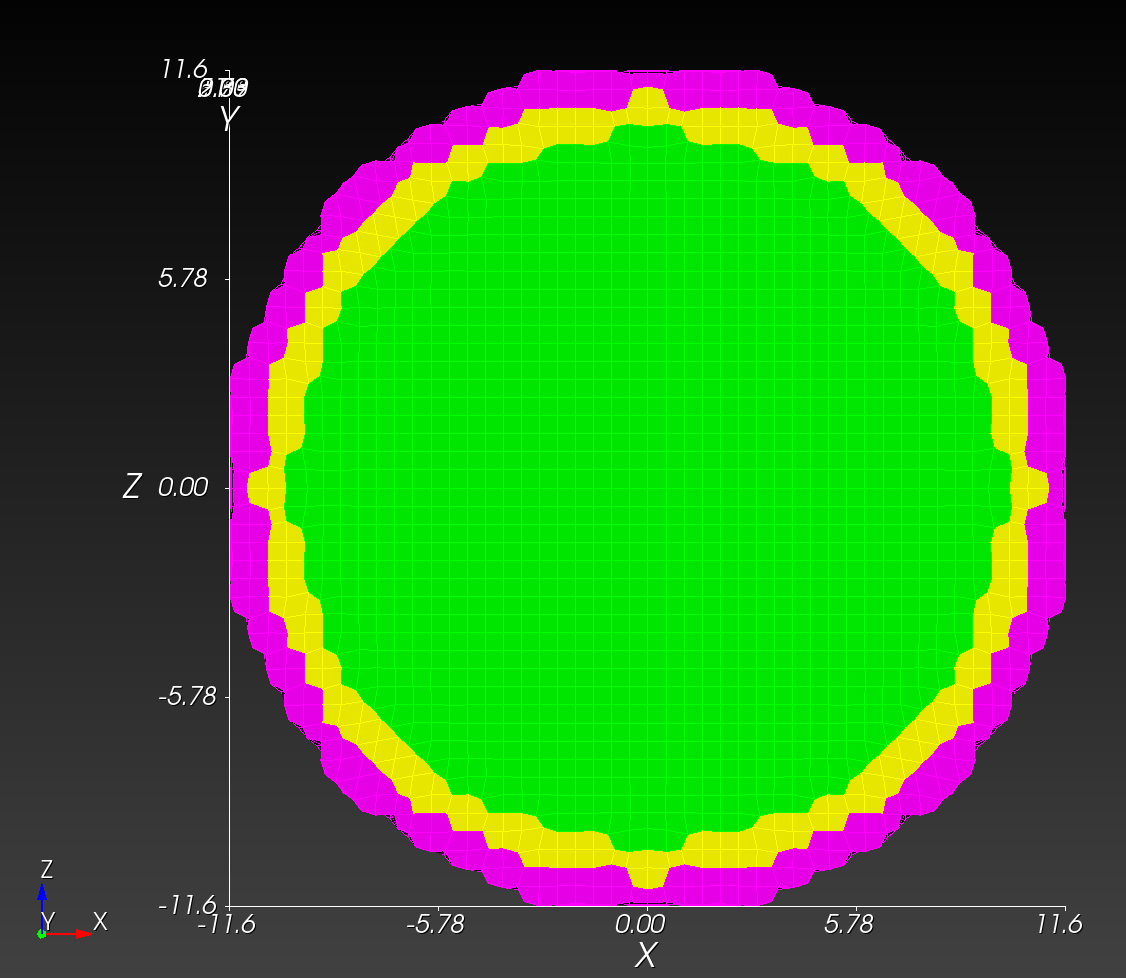 | 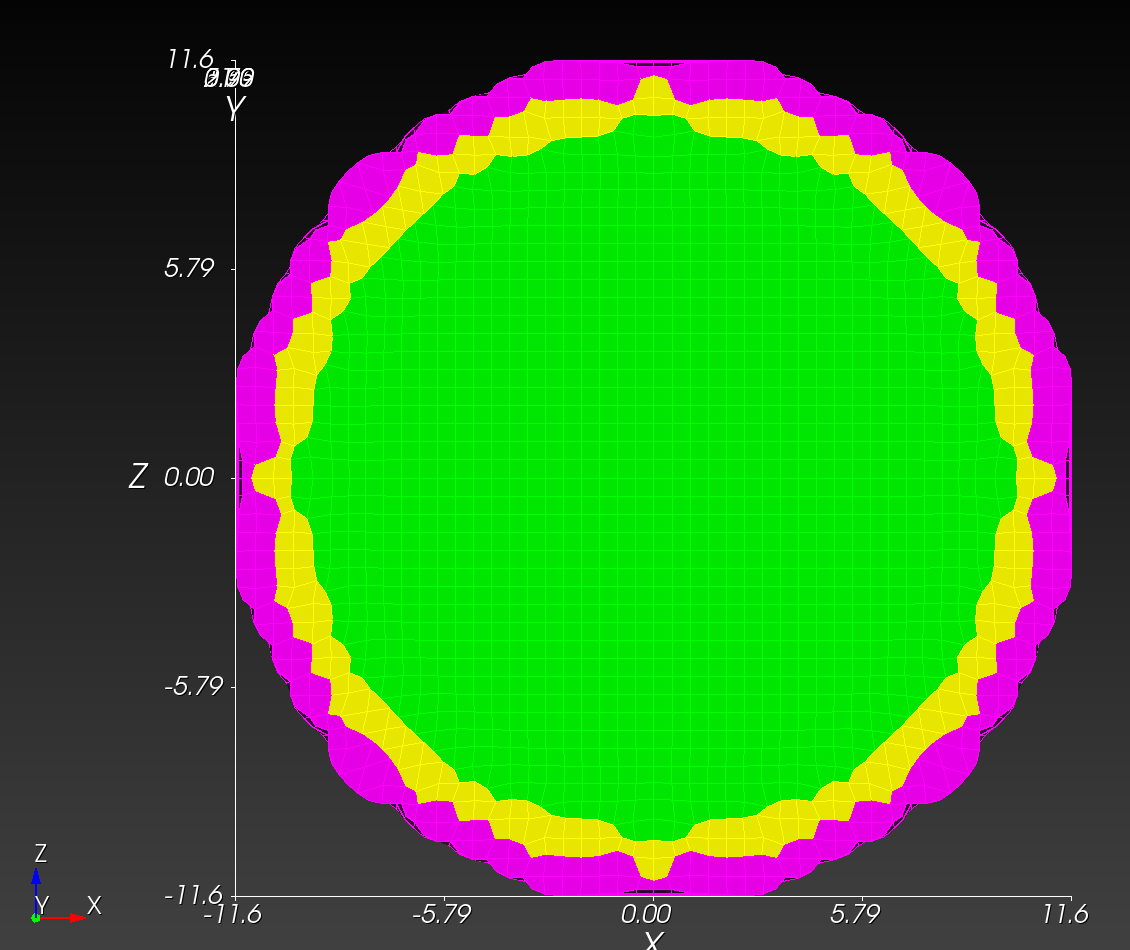 |
Smooth with various number of iterations:
automesh mesh hex \
--remove 0 \
--xscale 0.5 --yscale 0.5 --zscale 0.5 \
--xtranslate -12 --ytranslate -12 --ztranslate -12 \
--input spheres_resolution_2.npy \
--output sr2s10.exo \
smooth \
--hierarchical \
--iterations 10
automesh mesh hex \
--remove 0 \
--xscale 0.5 --yscale 0.5 --zscale 0.5 \
--xtranslate -12 --ytranslate -12 --ztranslate -12 \
--input spheres_resolution_2.npy \
--output sr2s50.exo \
smooth \
--hierarchical \
--iterations 50
Quality Metrics
Assess element quality to avoid oversmoothing:
automesh mesh hex \
--remove 0 \
--xscale 0.5 --yscale 0.5 --zscale 0.5 \
--xtranslate -12 --ytranslate -12 --ztranslate -12 \
--input spheres_resolution_2.npy \
--output sr2s10.inp \
smooth \
--hierarchical \
--iterations 10
automesh metrics \
--input sr2s10.inp \
--output sr2s10.csv
automesh mesh hex \
--xscale 0.5 --yscale 0.5 --zscale 0.5 \
--xtranslate -12 --ytranslate -12 --ztranslate -12 \
--input spheres_resolution_2.npy \
--output sr2s50.inp \
smooth \
--hierarchical \
--iterations 50
automesh metrics \
--input sr2s50.inp \
--output sr2s50.csv
With figio and
the hist_sr2sx.yml recipe,
cd ~/autotwin/automesh/book/analysis/sphere_with_shells/recipes
figio hist_sr2sx.yml
we obtain the following element quality metrics:
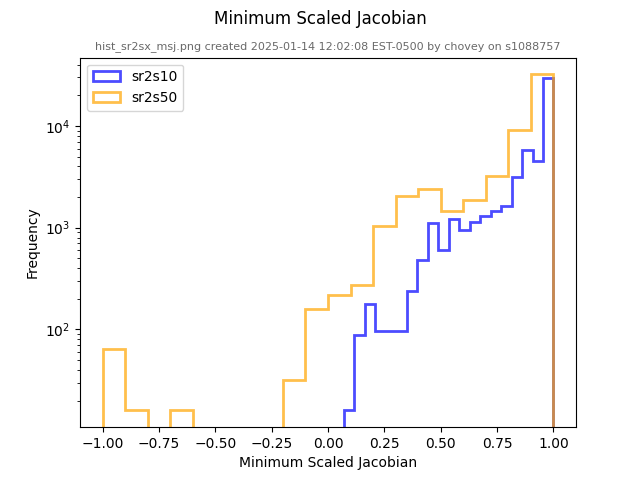
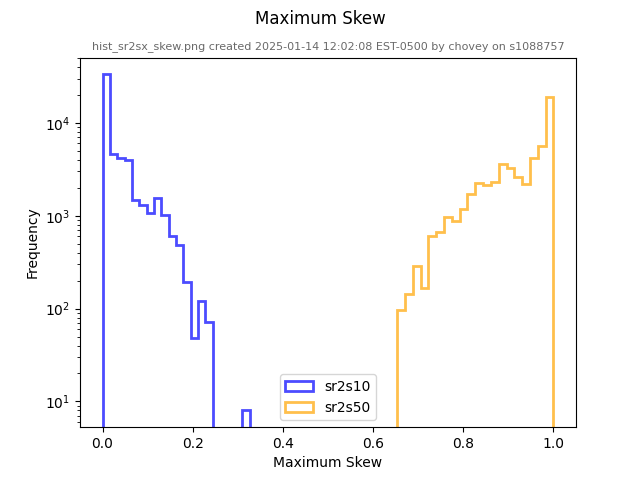
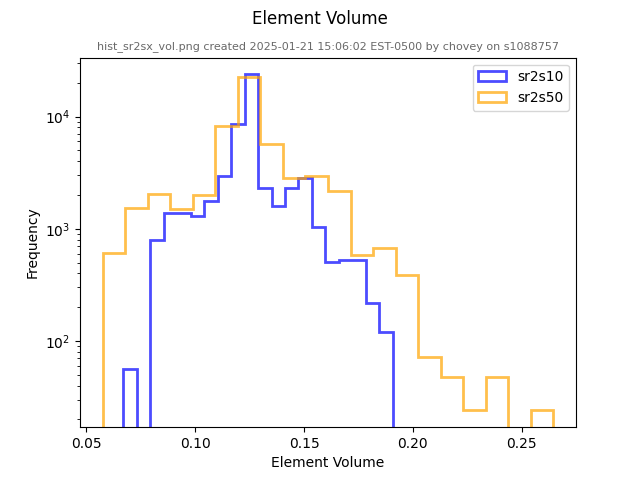
Comparisons
Conforming versus Segmented Meshes
We define a conforming mesh as a traditional finite element mesh that has nodal placement on the boundary of the geometry approximated by the mesh. A conforming mesh has a piecewise approximation of the curvature on the boundary.
In contrast, a segmented mesh (also known as a voxelized or "sugar-cube" mesh) is composed of voxels that approximate the boundary in a "stair-step" fashion, with nodal placement fixed on a regular, uniform grid of cube-shaped elements. A segmented mesh has a stair-step approximation of the curvature on the boundary.
The meshes from the Sphere with Shells section illustrate these two mesh types:
| conforming | segmented |
|---|---|
 |  |
 |  |
Both the conforming and segmented meshes approximate the true geometry: a sphere with concentric shells. Both approaches introduce error when used in finite element analysis in the calculation of quantities of interest, such as stress and strain.
We are interested in comparing the two methods, and quantifying what error the segmented approach introduces relative to the conforming approach.
For the spheres with shells example above, we were able to readily create two de novo meshes (the conforming mesh and the segmented mesh). There are instances, however, where a traditional, conforming finite element mesh exists, but a segmented version of the same geometry does not exist.
To create a segmented version of a conforming mesh, we created the segment command. Following are a examples using the segment functionality.
Recovering the Segmented Sphere
We use the conf_0.5cm.g file as our start point. See the Mesh Creation and Visualization section for a download link. Our objective it to recover the segmented version of the model, shown above, using the segment command.
# Clone the .g to .exo
cp conf_0.5cm.g conf_0.5cm.exo
automesh segment hex -i conf_0.5cm.exo -o conf_0.5cm_vox_segmented_g2_s0p5.exo -g 2 -s 0.5
automesh segment hex -i conf_0.5cm.exo -o conf_0.5cm_vox_segmented_g2_s0p5.inp -g 2 -s 0.5
The resulting mesh from conf_0.5cm_segmented_g2_s0p5.exo is shown (with a cut plane to show the interior) below:
| midline | isometric |
|---|---|
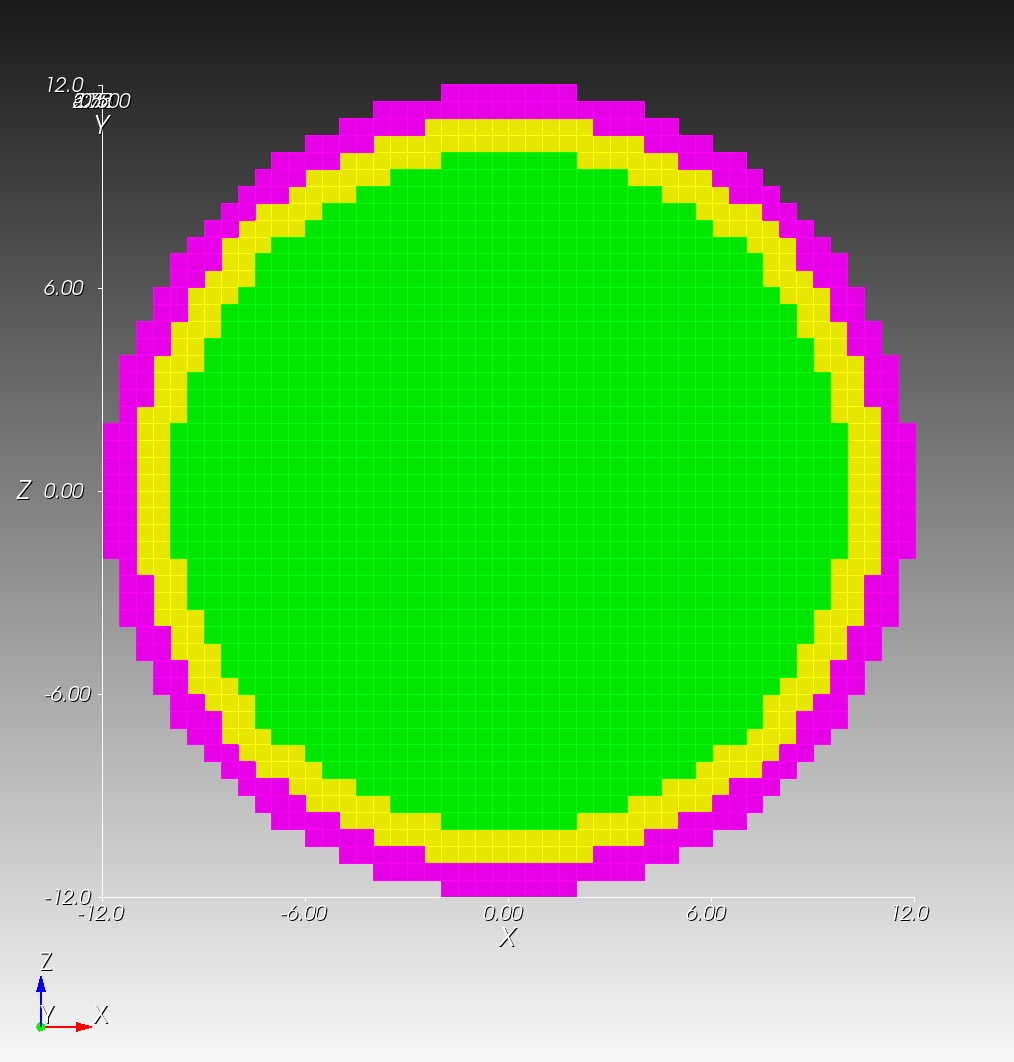 | 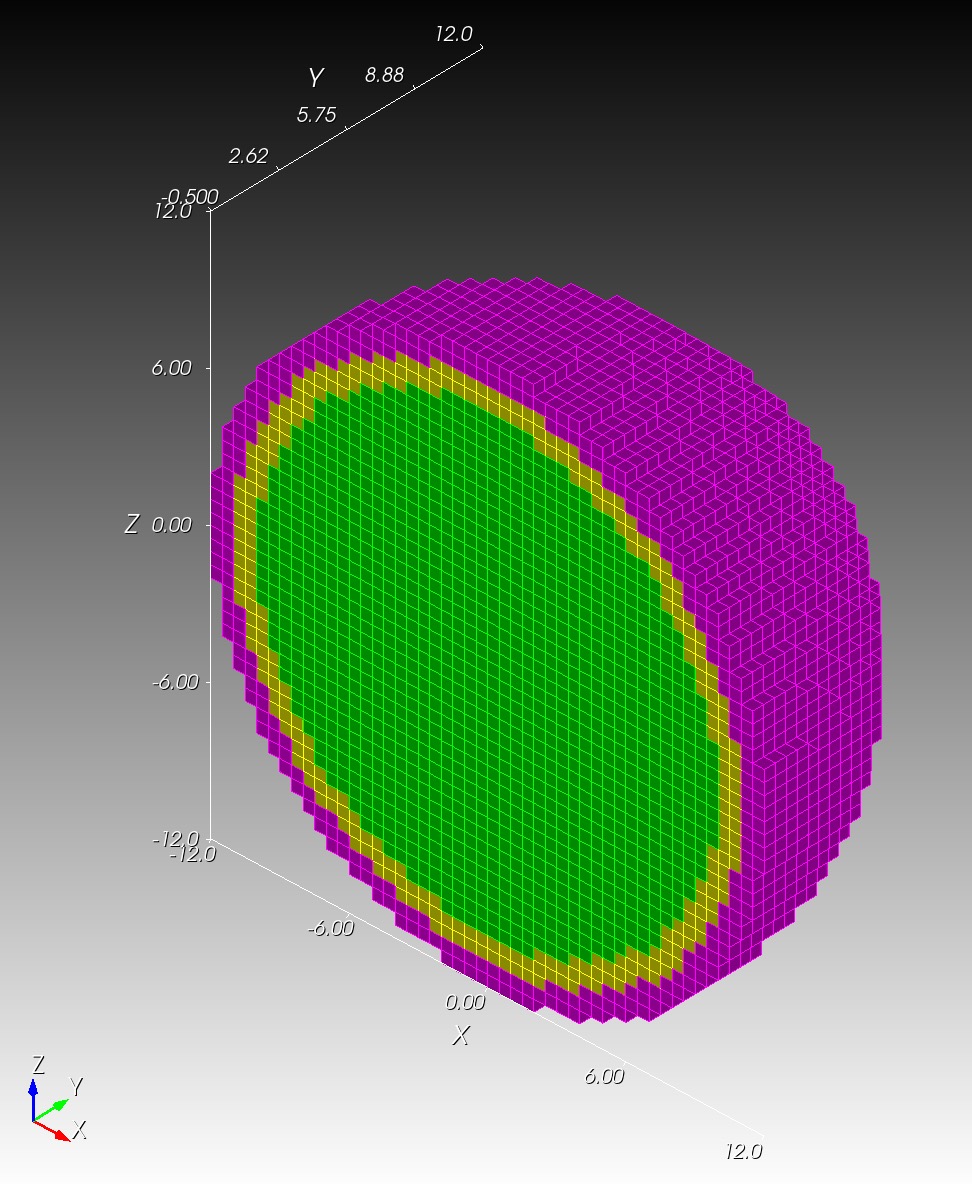 |
The conf_0.5cm_segmented_g2_s0p5.inp file mesh matches conf_0.5cm_segmented_g2_s0p5.exo exactly. Note that these new segmented meshes are slightly different from the original segmentations since they are created from a conforming mesh source.
RMU Brain Model
The RMU brain model, All_Hex_Dec, is a model of a human head.
Source Files
| file | md5 checksum | size |
|---|---|---|
All_Hex_Dec.inp | 4e376f7d551890b807cabc1d89630772 | 212 MB |
All_Hex_Dec.exo | 5df6f584a30139cb89e6e6917f843f55 | 66 MB |
test_1_1.exo | 5c0f02a7960890ffbe536493c4993104 | 95 MB |
test_1_2.exo | db674b42065cd9de9c8eb30ce2945c0f | 13 MB |
test_1_3.exo | 50da29122a0435672e62156308120ea9 | 4 MB |
test_2_1.exo | d108b4fe0aa524610fbe036e337fc6e1 | 105 MB |
test_3_0p8.exo | 60dddb70a9b018b4a25a35850c676eb6 | 205 MB |
test_3_0p8.inp | 63da6d1266a86561209ccda5f69bca23 | 541 MB |
The model has 12 blocks composing the various anatomy of the head and brain, shown below.
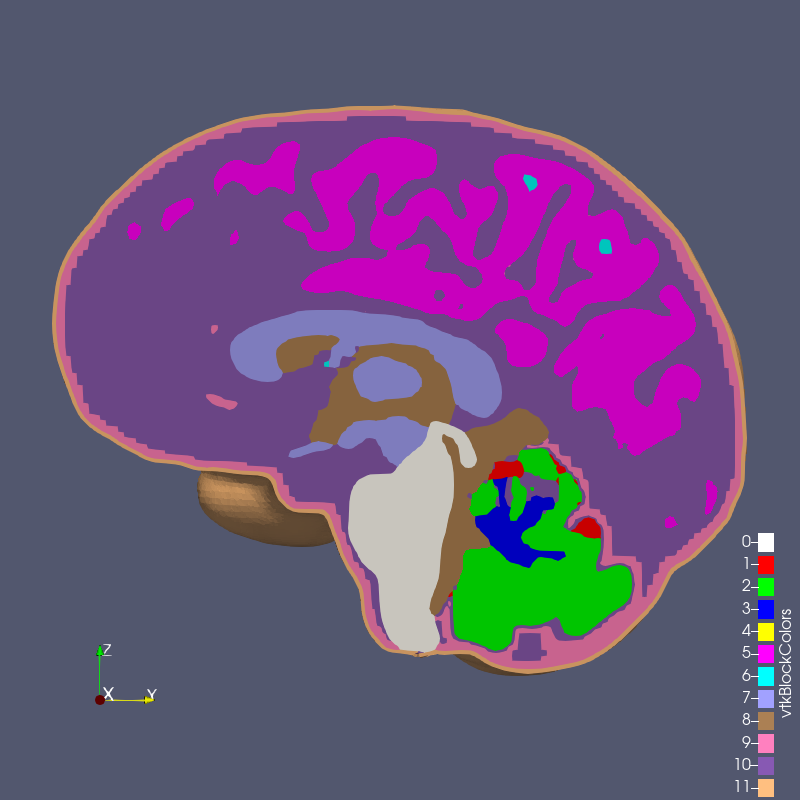
Figure: RMU brain model All_Hex_Dec.exo
With this conforming mesh, we create segmented meshes with the segment command, for example,
automesh segment hex --input All_Hex_Dec.exo --output test_3_0p8.exo --grid 3 --size 0.8
The output files have the naming convention test_x_y.exo where
xis the grid number,yis the element length in mm,- and
0p8means0.8 mm.
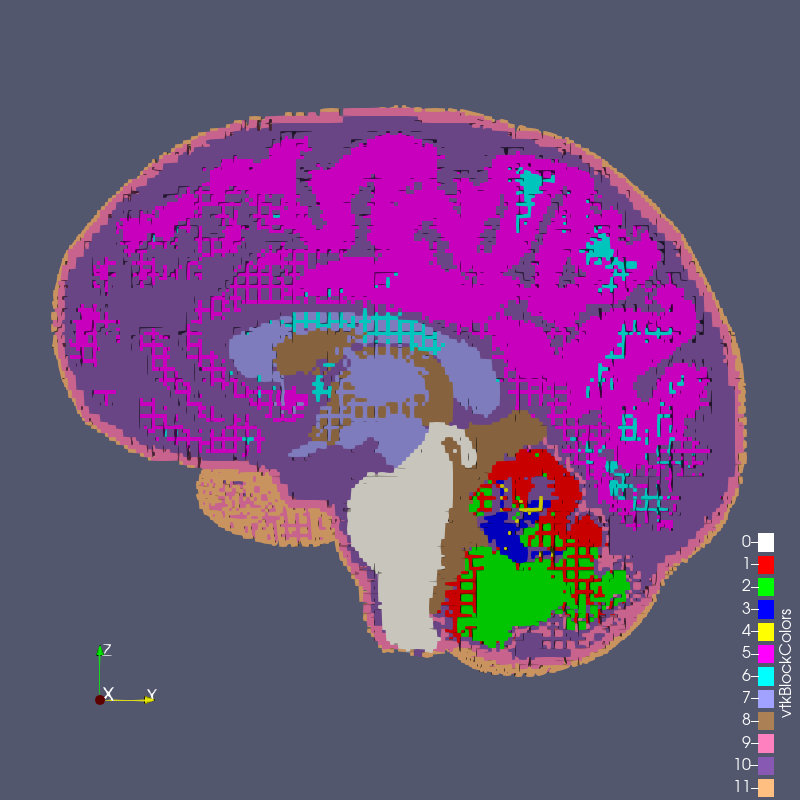
Figure: test_1_1.exo created with options --grid 1 --size 1

Figure: test_1_2.exo created with options --grid 1 --size 2

Figure: test_1_3.exo created with options --grid 1 --size 3
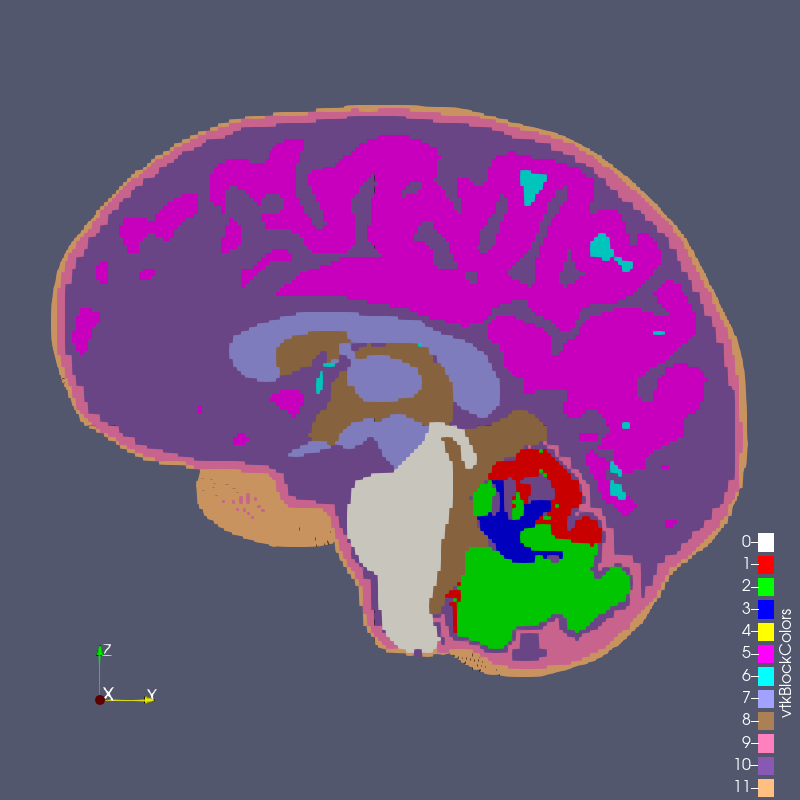
Figure: test_2_1.exo created with options --grid 2 --size 1
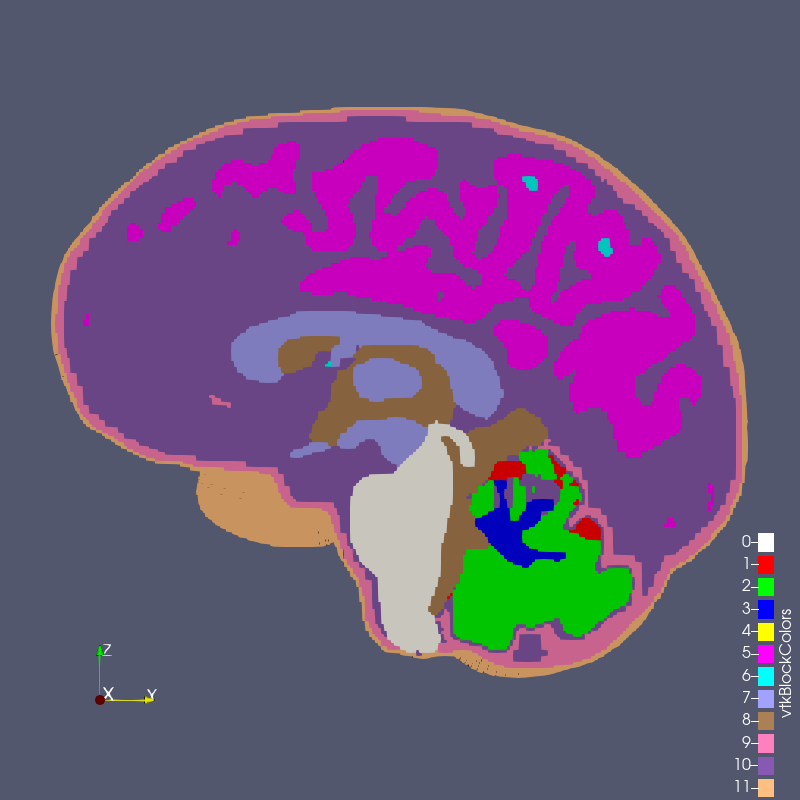
Figure: test_3_0p8.exo created with options --grid 3 --size 0.8
Comparison
All_Hex_Dec.exo | test_3_0p8.exo |
|---|---|
 |  |
Development
Prerequisites
Optional
- VS Code with the following extensions:
- GitHub CLI
Development Cycle Overview
- Branch
- Develop
cargo build- Develop:
- tests
- implementation
- Document:
mdbook build- output:
automesh/book/build
- output:
mdbook serve --open- interactive mode
- On the local machine, with Firefox, open the
index.htmlfile, e.g.,file:///Users/chovey/autotwin/automesh/book/build/index.html
- Test:
cargo testcargo run// test without required input and output flagscargo run --release -- -i tests/input/f.npy -o foo.exocargo run -- --help
- Pre-commit:
pre-commit run --all-files
- Clean:
cargo clean
cargo doc --open
- Test
maturin develop --release --features python
- Merge Request
Environment Modules
The automesh application can be installed as a service on a High-Performance Computing (HPC) system with the following steps:
Install and Compile Application
automesh must be available and installed to a file location that is accessible by all compute nodes and users who need it.
- Location: Choose a central directory such as
/opt/hpc/or/sw/for theautomeshbinaries, libraries, and associated files. For example, let's assume the install path is/opt/hpc/apps/automesh/0.3.7. - Compilation: Compile
automeshand all its dependencies statically if possible, or ensure all shared libraries (.sofiles) are also included in the installation directory structure.
Create a Module File
The module file, a small script usually written in Tcl or Lua, provides the module load functionality. It tells the shell what changes to make to the user's environment when the module is loaded.
- Location: Module files are placed in a specific directory structure that is scanned by the Environment Modules software (e.g., Lmod or Tcl-based modules). A common path would be
/opt/hpc/modules/automesh/0.3.7.
A typical module file would be something like this:
#%Module
# Define the application name and version
set name automesh
set version 0.3.7
# 1. Prerequisite check (e.g., automesh needs a specific compiler)
# If your app needs a specific compiler, you can ensure it's loaded first:
# prereq gcc/11.2
# 2. Update the PATH variable
# This is the most critical step, allowing the user to run 'automesh' command
prepend-path PATH /opt/hpc/apps/$name/$version/bin
# 3. Update the LD_LIBRARY_PATH variable
# Allows the application to find shared libraries if not statically linked
prepend-path LD_LIBRARY_PATH /opt/hpc/apps/$name/$version/lib
# 4. Define other environment variables (optional)
# For configuration files, data paths, etc.
setenv MYAPP_HOME /opt/hpc/apps/$name/$version
# 5. Provide a short description (optional)
module-whatis "Loads $name $version, a high-performance compute application."
System Configuration
Finally, an HPC administrator needs to ensure that the directory containing the new module file
is known to the module system. The administrator must add the root of your module directory
(e.g., /opt/hpc/modules) to the central module configuration, typically via a command such as:
module use /opt/hpc/modules
This is usually done in a global system profile script so it is active for all users.
End User
Users can discover and load automesh:
- Check for the module:
module avail automesh - Load the service:
module load automesh/0.3.7(ormodule load automeshif it is the default) - Run the program:
automesh --version
References
-
As of Oct 2024,
cmakeis required forhdf5-metno-src v0.9.2, used for writing Exodus II files. On macOS withbrew, install withbrew install cmakeinstead of the GUI installer. ↩
Python Development
Install Python
Install a Python version supported by automesh.
Install Rust as well.
Create a Virtual Environment
Note: If a virtual environment folder automesh/.venv already exists from previous installs, then remove it as follows:
cd automesh # from the automesh directory
(.venv) deactivate # if the virtual environment is currently active
rm -rf .venv # remove the virtual environment folder
# with `rm -rf .venv/`.
python -m venv .venv # create the virtual environment
# activate the venv with one of the following:
source .venv/bin/activate # for bash shell
source .venv/bin/activate.csh # for c shell
source .venv/bin/activate.fish # for fish shell
.\.venv\Scripts/activate # for powershell
pip install --upgrade pip
pip install maturin
Build and Test the Source Code
maturin develop --features python --extras dev
pytest
pre-commit run --all-files
uv run ruff check
Build a '.whl` file release
maturin build --release --features python
Lint the Source Code
cargo clippy --features python
pycodestyle --exclude=.venv . # exclude the .venv folder
Build and Open the API Documentation
pdoc automesh --math --no-show-source --template-directory docs/
Rust Development
Install Rust
Install Rust using rustup with the default standard installation:
curl --proto '=https' --tlsv1.2 -sSf https://sh.rustup.rs | sh
Rust updates occur every six week. To update Rust:
rustup update
Clone Repository
git clone git@github.com:autotwin/automesh.git
Build and Test the Source Code
cd automesh
cargo test
Lint the Source Code
cargo clippy
Build and Open the API Documentation
cargo rustdoc --open -- --html-in-header docs/katex.html
Run the Benchmarks
Execute benches/block.sh once, and subsequently run
rustup run nightly cargo bench
Review of Tong et al. 2024
@article{tong2024hybridoctree_hex,
title={HybridOctree\_Hex: Hybrid octree-based adaptive all-hexahedral mesh generation with Jacobian control},
author={Tong, Hua and Halilaj, Eni and Zhang, Yongjie Jessica},
journal={Journal of Computational Science},
volume={78},
pages={102278},
year={2024},
doi = {10.1016/j.jocs.2024.102278},
url = {https://doi.org/10.1016/j.jocs.2024.102278},
publisher={Elsevier}
}
- GitHub repo
Octree Initialization with Feature Preservation
- Target surface
- Octree
- Refinement
- Curvature (not as robust as SDF, noisy)
- Narrow region
- Shape diameter function (SDF, Michael: works more robust)
- Refinement
- Dualization
- Removal
- Vertex clearing rule
- Signed distance function
- Face normals
- Conformity
- Node duplication and projection
- Augmentation (similar but still different from pillowing)
- Energy minimization (different from Internal Energy)
- Geometry fitting
- Minimum scaled Jacobian (for postive-Jacobian hexes)
- Jacobian (for negative-Jacobian hexes)
0. Target Surface
Input:
- Target Surface: A closed and manifold surface mesh composed of a 3D triangular elements.
- See the HybridOctree_Hex/input boundaries folder for boundary raw files, e.g.,
Cup1_tri.raw...wrench_tri.raw. - Alternatively, might
.stlfiles be available? - For example,
bunny_tri.raw(33,739 lines, 618kB) has the format (11,248 points, 22,490 elements):
- See the HybridOctree_Hex/input boundaries folder for boundary raw files, e.g.,
11248 22490 # line 1
0.121904 0.714156 0.831321 # line 2, coordinates
0.121904 0.714156 0.831321
0.943086 1.00012 1.6947
...
0.263885 1.15905 1.42424
0.389988 0.897909 1.43231
0.268144 0.793896 1.27816 # line 11249
7752 1374 1 # line 11250, connectivity
1 1374 10841
3831 7752 1
...
10983 11126 11129
11149 11061 11102
11220 11234 11103 # line 33739
Based on the README.md, the resulting bunny hexahedral FEA mesh has 26,375 vertices, 21,695 elements, and a minimum scaled Jacobian of 0.57.
1. Octree: Refined, then Strongly Balanced
The octree is refined at regions of high curvature and narrow thickness.
- Curvature Detection: Gaussian curvature is calculated for surface points. Five thresholds are used. If a cell at level satisfies , it is refined to level .
- Narrow Region Detection: Thickness is measured via ray-casting. If (thresholds: ), the cell is refined.
The resulting octree levels for each octant typically range from level 5 to 9.
After the initialization, the octree is updated with the following two rules to ensure that the octree is strongly balanced:
- Balancing Rule: The level difference between neighboring octants must be at most one.
- Paring Rule: If an octant is subdivided to meet the balancing rule, its seven siblings must also be subdivided.
2. All-Hex Dual Mesh
Five pre-defined 3D templates are used to directly extract an all-hexahedral dual mesh.
- Hanging Nodes: These occur at transitions between different resolution levels.
- Templates: The system detects transition faces (shared by two cells of different levels) and transition edges (shared by three cells).
- The 5 Templates:
- One (1) handles face transitions and
- Four (4) handle various edge transition configurations.
- This ensures every grid point is shared by exactly eight polyhedra, resulting in a valid hex mesh.
The minimum scaled Jacobian for the templates is 0.258, which is the starting point before Section 4 optimization.
3. Buffer Zone Clearing and Geometric Restriction
The core mesh is the subset of the dual mesh that fits completely within the target volume. It is the largest possible assembly of dual hexes that fits entirely within the target volume while leaving a small gap (the buffer zone) for boundary alignment.
- The core mesh has a blockly (synonyms: jagged, stair step, sugar cube) appearance.
- The core mesh is created by removing elements from the dual mesh that lie outside or too close to the target surface.
A boundary point is any vertex that lies on the outer (quadrilateral) surface of the core mesh.
The buffer zone is the empty region between the jagged outer boundary of the core mesh and the target surface.
3.1 Clearing
The clearing process intentionally removes elements that are potentially too close to the target surface, which could result in a lower quality element.
If we were to keep every hex that is technically "inside" the target surface, some of the core hexes would have vertices that nearly touch the target boundary. Then, in later steps, when we connect these core vertices to neighboring vertices on the surface, a paper-thin (e.g., 1 percent thickness) element would be created, leading to a bad scaled Jacobian, or even an inverted element if the vertex accidentally crosses the boundary during optimization.
Vertex Clearing Function
Let
- be the maximum size (typically as maximum edge length) of all elements sharing a vertex.
- size threshold .
Then,
- Vertex clearing rule: If the minimum distance between from a vertex to the boundary falls below the size threshold , all elements sharing that vertex are deleted.
By setting the threshold to half of the size of the largest local element (), the algorithm ensures that the "gap" (the buffer zone) is of substantial size. This half-size rule effectively "erodes" the core mesh until there is a guaranteed clearance. It also ensures tha the final "buffer layer" hexes have a healthy aspect ratio (roughly or better) before the optimization begins.
In short, clearing eliminates interior volume of the core mesh to make room for high-quality boundary hexes. Without this elimination step, the mesh would likely fail in thin or high-curvature regions.
Signed Distance Function (SDF)
The authors then noted, "During implementation, we observed that this setting [the vertex clearing rule] can be sensitive to large elements located in size transition regions, potentially leaving holes in the surface. To address this issue, we calculate the signed distance function for corner points associated with every hex element. Each hex had eight signed distance functions , where . We compute and and remove the hex element if the condition is met."
To illustrate this problem imagine a large hex sitting next to small hexes (a size transition). If a single vertex of the large hex is flagged as "too close" to the target surface, the vertex clearing rule forces the deletion of the entire large hex. Because the hex is large, a massive chunk of the model's interior gets deleted, leaving behind the smaller neighboring hexes that likely are unable to "fill" the gap easily, resulting in a hole or a broken surface of the final mesh.
The authors replaced the brittle vertex clearing rule with the SDF reult. (Personal communication with Tong on 2026-02-24 indicates they used both the vertex clearing function and the signed distance function). While the vertex clearing rule removed everything based on a single vertex rule, the SDF considers all eight corners of a specific hex to decide if it should be eliminated or not.
The weighted decision formula, acts as a soft-boundary filter.
Let
- be a closed, orientable 2-manifold surface in .
- A 2-manifold surface is a topological space that, at every point, looks locally like a small piece of the 2D Euclidean plane ().
- be a query point (e.g., a corner of a hex element).
- be the closest point on the surface to .
- is the inward-pointing (not outward-pointing as is typically defined) unit normal vector of the surface at the closest point .
- If lies on a triangle face of , then a simple face-normal is used.
- If lies on an edge or on a vertex, a pseudo-normal, which is weighted combination of the normals of the adjoining faces sharing the vertex or edge, is used.
- Use of the inward-pointing normal is referred to as the "material convention", which is different from the standard convention.
- is the signum function:
The Signed Distance Function (SDF) for is defined as:
where:
- The magnitude is the shortest Euclidean distance from the query point to the manifold. It is always non-negative.
- The direction vector points from the closest point on the surface to the query point.
- Outside the surface:
- If the query point lies outside of the surface, the vector points opposite of the surface inward normal
in the same general direction as the surface outward normal, making the dot product negative and .
- If the query point lies outside of the surface, the vector points opposite of the surface inward normal
- Inside the surface:
- If the query point lies inside of the surface, the vector points in the same general direction as the surface inward normal , making the dot product positive and .
- On the surface:
- If is on the surface, , the distance is , and the dot product is zero, thus .
- Outside the surface:
We remove a hex if .
Note the definition of a signed distance must be reversed to keep the core and remove the outside. There is a slight reversal in the standard mathematical definition of SDF and the removal formula in the paper.
The paper cites Paragios et al. 2002, which likewise in Section 2 of their paper defines positive values to be inside the region defined by shape ; and negative values to be outside of the region .
If one uses the standard mathematical definition ( is outside) with the paper's formula (), one will delete the interior of the model and keep the empty air around it.
Sign Reversal: For the paper's criterion to work as intended (to keep "core" and remove "outside"), the paper must be used with the material convention:
- Inside (positive distance into the material)
- Outside (negative distance into the void)
Examples:
The following example test the logic of the "material convention" (positive = inside), and illustrate why is so clever when positive is inside.
- Scenario A: Deeply Inside
- All 8 corner of the hex have .
- . Since is not , the hex is retained.
- Scenario B: Deeply Outside
- All 8 corner of the hex have .
- . Since the hex is removed.
- Scenario C: Straddling (but mostly outside)
- (far outside), (barely inside).
- . Since , the hex is removed.
- Scenario D: Straddling (but mostly inside)
- (barely outside), (deeply inside).
- . Since 0.5 is not , the hex is retained.
Insight: The foregoing "weighted" rule allows a hex to stay even if a corner poke slightly out, as long as the rest of the hex is deeply buried inside. This is exactly what prevents "holes" in size-transition regions.
3.2 Restriction
Simply having the valid core mesh is not sufficient:
- If angles between the faces surrounding a boundary point are too sharp, the new hexes created in the buffer zone will be inverted or of extremely poor quality.
Boundary point to target surface
- Connectivity: A boundary point is shared by quadrilateral faces that form the external surface of the core mesh.
- Role in Meshing: Every boundary point is eventually connected to its closest point on the target surface via an edge vector . This connection
"stretches"augments the mesh to fill in the buffer zone.
The normal vector is defined as the normal of a triangle formed by boundary point and two of its adjacent boundary points.
The Restriction: To prevent poor-quality elements when connecting to the target surface, a normal-based restriction is enforced. For a boundary point , any three normals (, , ) of the surrounding faces must satisfy .
- Iterative Removal: Hexes are deleted one-by-one until all boundary points satisfy this geometric restriction.
- This restriction guarantees that the remaining boundary points have a geometry that guarantees a scaled Jacobian for the final boundary elements.
- Deletion Priority: The algorithm prioritizes hexes with the highest number of boundary faces during buffer clearing to avoid creating internal holes.
4. Quality Improvement with Jacobian Control
The final step meshes the buffer zone by connecting core boundary points to their closest surface points and optimizing the resulting elements.
- Smart Laplacian Smoothing: Performed every 1,000 iterations on the outermost two layers to speed up convergence.
- Energy Minimization: A gradient-based method minimizes an energy function :
or, more compactly,
or, more explicitly,
- Jacobian Control: Because the Scaled Jacobian is non-differentiable in certain regions, the algorithm switches to the Jacobian term for negative-Jacobian elements to ensure they can be untangled.
- The paper specifically identifies (the Jacobian term) as the mechanism to untangle elements with negative Jacobians.
- Using a combined scaled Jacobian and Jacobian helps the optimizer not to get stuck in local minima.
- The novel buffer zone clearance and mesh quality enhancements lead to significantly higher minimum scaled Jacobian .
- Signage: Since the goal is to minimize , the two Jacobian-related terms are subtracted since the optimization is actually trying to maximize the Jacobian-terms (improve mesh quality) while trying to minimize the distance between the mesh and the surface.
Gradient
Let be any vertex belonging to the boundary of the core mesh composed of dual hexahedral elements.
Let point be the closet point projection of node onto surface .
In general, and . We seek to make the domain's boundary conform to surface .
Let the gap vector from the closet point projection to the hexahedral vertex be defined as:
The objective of the surface energy is to characterize the gap energy between surface and the domain boundary in a pointwise manner.
Let this surface energy mismatch be defined as
for the surface vertices, then the gradient at is simply
The term acts as a spring that pulls the current vertex toward its target surface position .
Gradient
For any hex elements that have a negative Jacobian, we seek to maximize the Jacobian energy term , which will tend to move the Jacobian from negative to positive (untangling).
For any hexahedral element, we evaluate the Jacobian at node . We denote the three edge-sharing vertices as .
The Jacobian is defined as
It will be more convenient to define edge vectors as follows:
Then, the Jacobian is defined as
To find the gradient of the Jacobian energy with respect to the position of vertex , we need to differentiate the scalar triple prodcut. The gradient is a vector that describes how the volume (i.e., the Jacobian) changes as the position of node changes.
By applying the product rule for cross and dot products, we find:
Note that (and similarly for and ), which introduces a negative sign into the derivatives.
Each term in the gradient represents a vector area of one of the faces meeting at node :
- is the normal vector to the face formed by .
- is the normal vector to the face formed by .
- is the normal vector to the face formed by .
The gradient is simply the negative sum of these three face normals:
In terms of the gradient descent update, , we update the position of element node as follows
The update moves in the direction of the sum of the adjacent face normals. The update effectively "pushes" node out of the plane of its neighbors to maximize the volume and resist element inversion.
The Jacobian and its gradient can be calculated for each of the eight element nodes per hex, as well as in the element center, where the edge vectors connect the opposite face centers.
Gradient
For any hex elements that have a positive Jacobian, we seek to maximize the scaled Jacobian energy term , which will drive the MSJ toward their maximum value of unity.
Once the hexes transition from negative to positive Jacobian (they thus become untangled, ), we cease using these hexes the term, considering them instead as participants in the term.
The normalized version of the Jacobian, the scaled Jacobian is defined as
or, using the edge vector definitions defined previously,
The gradient requires the quotient rule to account for the changing edge lengths in the denominator. Let
which is the product of the three lengths. Then
and
where the length gradient term is:
Like the Jacobian, the scaled Jacobian and its gradient can be calculated for each of the eight element nodes per hex, as well as in the element center, where the edge vectors connect the opposite face centers.
Gradient Descent
At iteration , we update the position of by an amount , where is the step size (also known as the learning rate), which controls how far the vertex moves in a single iteration:
Tong et al. choose for all tested models in their paper.
Plot of Jacobian and Scaled Jacobian - Orthogonal Case
import numpy as np
import matplotlib.pyplot as plt
# Define nodes a, b, c (orthogonal)
a = np.array([1, 0, 0])
b = np.array([0, 1, 0])
c = np.array([0, 0, 1])
# Initial x and arbitrary direction d
x0 = np.array([0, 0, 0])
d = np.array([1, 0.5, 0.2]) # Arbitrary direction
d = d / np.linalg.norm(d) # Normalize
t_vals = np.linspace(-2, 4, 400)
def compute_metrics(t):
"""Compute Jacobian and Scaled Jacobian for a given displacement t."""
x = x0 + t * d
u = a - x
v = b - x
w = c - x
# J = (u x v) . w
j = np.dot(np.cross(u, v), w)
# L = ||u|| * ||v|| * ||w||
l_denom = np.linalg.norm(u) * np.linalg.norm(v) * np.linalg.norm(w)
# Scaled Jacobian
sj = j / l_denom if l_denom != 0 else 0
return j, sj
results = [compute_metrics(t) for t in t_vals]
j_vals, sj_vals = zip(*results)
# Create a combined plot of Jacobian and Scaled Jacobian where scaled Jacobian
# is usesd if the Jacobian is positive, and the Jacobian is used if it is negative.
# Create combined_j_sj_vals: use sj if sj > 0, else use j
combined_j_sj_vals = [sj if sj > 0 else j for j, sj in zip(j_vals, sj_vals)]
# Create the plot
plt.figure(figsize=(10, 6))
plt.plot(
t_vals,
combined_j_sj_vals,
label="Combined ($J$ or $\hat{J}$)",
color="orange",
linewidth=7,
alpha=0.5,
)
plt.plot(t_vals, j_vals, label="Jacobian ($J$)", color="blue", linewidth=2, alpha=0.7)
plt.plot(
t_vals,
sj_vals,
label="Scaled Jacobian ($\hat{J}$)",
color="magenta",
linestyle="--",
linewidth=2,
alpha=0.7,
)
# Styling
plt.axhline(0, color="black", linewidth=0.8, linestyle="-")
# plt.axvline(0, color="gray", linewidth=0.8, linestyle="-")
# Ideal target line (Green at y = +1)
plt.axhline(
1, color="green", linewidth=1.0, linestyle="--", zorder=0, label="Ideal ($y=1$)"
)
# Lower bound limit (Red at y = -1)
plt.axhline(
-1,
color="red",
linewidth=1.0,
linestyle="--",
zorder=0,
label="Inverted Limit ($y=-1$)",
)
plt.xlabel("Displacement $t$ along arbitrary direction $\mathbf{d}$", fontsize=12)
plt.ylabel("Metric Value ($J$ and $\hat{J}$)", fontsize=12)
plt.title("Jacobian and Scaled Jacobian as Node $\mathbf{x}$ Moves", fontsize=14)
plt.legend()
plt.grid(True, alpha=0.3)
# Set the y-axis ticks explicitly
plt.yticks([-4, -3, -2, -1, 0, 1, 2, 3, 4])
# Save image
plt.savefig("jacobian_and_scaled_jacobian.png")
plt.show()
The Jacobian is a linear function of the displacement . The curve is straight because the volume of a parallelpiped (or tetrahedron) changes linearly with the distance of one vertex from the plane formed by the other three. The zero crossing is where the line crossed the -axis, representing the moment node enters the plane of its neighbors . Beyond this point, becomes negative and the the hex element is inverted.
The scaled Jacobian is a nonlinear function because the denominator contains the lengths of the edges (square roots of quadratic functions). The curve is bounded between . As the node moves very far away, the scaled Jacobian will grow toward zero as the angles between the edges become extremely sharp. The peak of the curve represents the ideal position for node relative to its neighbors, and this peak will approach a value of unity for the orthogonal case.
The above plot explores node moving along a line parameterized by time as:
where is an arbitrary direction and = , and the Jacobian functions take the forms
- a linear function,
- a nonlinear curve, where are quadratic polynomials
Plot of Jacobian and Scaled Jacobian - Monte Carlo
To visualize an entire family of nodal positions, we use a Monte Carlo simulation. We perturb positions and vary the direction of vector on a unit sphere to generate a bundle of curves that represent a range of possible behaviors in a real, distorted mesh.
The plot below shows the Monte Carlo results.
The Monte Carlo view shows why the learning rate must be chosen carefully.
- Consistency: For the Jacobian, the gradient (slope of the blue lines) is constant for a given configuration.
- Sensitivity: For the scaled Jacobian, the gradient changes rapidly. Near , the current position, the curves are steep, meaning that small moves have a large image on quality.
- Global Maximum: The overlap of these curves suggest that in a complex mesh, there is no single "perfect" direction. The optimizer must balance many competiting and terms simultaneously.
A two-domain, piecewise approach
The Piecewise Energy Function is defined based on the Jacobian value being positive or negative. One can define the quality energy for a single hexahedron by checking the sign of its Jacobian . This ensures that "tangled" (inverted) elements are prioritized for unfolding before they are refined for shape quality.
where
- is the quality energy for a single hex .
- is the standard Jacobian (signed volume).
- is the scaled Jacobian (normalized shape metric).
- is a small positive tolerance (e.g., ) used to identify inverted or degenerated elements.
Since gradient descent minimizes energy, we subtract the quality metric to maximize it.
References
- Rousson M, Paragios N. Shape priors for level set representations. InEuropean Conference on Computer Vision 2002 Apr 29 (pp. 78-92). Berlin, Heidelberg: Springer Berlin Heidelberg. https://link.springer.com/chapter/10.1007/3-540-47967-8_6
- Signed Distance Functions and Ray-Marching, https://youtu.be/hX3mazz8txo?si=O7Ee81LF2REuf9WV
- Tong H, Halilaj E, Zhang YJ. HybridOctree_Hex: Hybrid octree-based adaptive all-hexahedral mesh generation with Jacobian control. Journal of Computational Science. 2024 Jun 1;78:102278. https://doi.org/10.1016/j.jocs.2024.102278
- Zhang Y, Liang X, Xu G. A robust 2-refinement algorithm in octree or rhombic dodecahedral tree based all-hexahedral mesh generation. Computer Methods in Applied Mechanics and Engineering. 2013 Apr 1;256:88-100. https://doi.org/10.1016/j.cma.2012.12.020
- Zhang Y, Bajaj C. Adaptive and quality quadrilateral/hexahedral meshing from volumetric data. Computer methods in applied mechanics and engineering. 2006 Feb 1;195(9-12):942-60. https://doi.org/10.1016/j.cma.2005.02.016