Isosurface

Isosurfacing is a method to extract the surface from a three-dimensional scalar field. A scalar field $\varphi =\varphi (x,y,z):{\mathbb{R}}^3\mapsto \mathbb{R}$, is a function that assigns a scalar value to every point in three-dimensional space. For the special case when all points in the domain $(x,y,z)\in {\mathbb{R}}^3$ are aligned into a regular (i.e., uniform) three-dimensional grid, the scalar field composes a voxel field.

The simplest example of non-trivial voxel field consists of a range of only two integer values, for example, 0 and 1, where 0 indicates a point in the grid is outside the field, and where 1 indicates a point in the grid is inside (or on the boundary of) the field. The interface between 0 and 1 everywhere in the grid composes the isosurface of the field.

Given a voxel field, the isosurface can estimated with two common techniques: Marching Cubes (MC) and Dual Contouring (DC). Lorensen and Cline¹ originally proposed MC in 1987. DC was originally proposed by Ju et al.² in 2002.

Marching Cubes

MC operates on each voxel in the 3D grid on a independent basis. For each voxel, the eight nodes of the voxel are evaluated as outside (0) the scalar field or inside (1) the scalar field. The eight nodes, classified as either 0 or 1, create 256 ($2^8$) possible configurations. Of these combinations, only 15 are unique configurations, after symmmetry and rotation considerations. For each configuration, MC generates a set of triangles to approximate the isosurface.

Advantages

• Simple implementation; uses only interpolation between voxel corners.
• Results in smooth surfaces because it interpolates along edges between voxel corners. This can be an advantage when smooth meshes are desired but is a disadvantage when sharp edges are desired.

Disadvantages

• Can produce ambiguous cases wherein the isosurface can be represented in multiple (non-unique) ways. This can result in a surface artifacts.
• Can produce non-manifold edges.

Manifold: "The mesh forms a 2D manifold if the local topology is everywhere equivalent to a disc; that is, if the neighborhood of every feature consists of a connected ring of polygons forming a single surface (see Figure 2 of Luebke³ reproduced below). In a triangulated mesh displaying manifold topology, exactly two triangles share every edge, and every triangle shares an edge with exactly three neighboring triangles. A 2D manifold with boundary permits boundary edges, which belong to only one triangle."

maniford	non-manifold

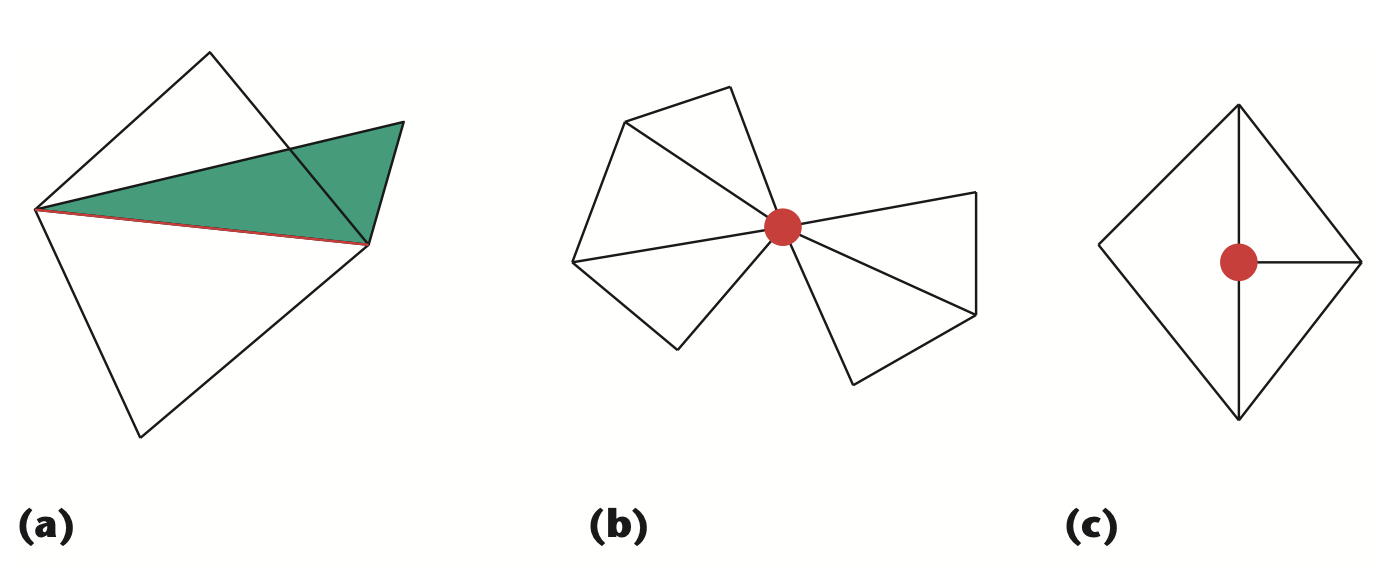Figure: Reproduction of Luebke³ Figure 2 (left) showing a manifold mesh, and Figure 3 (right) showing a non-manifold mesh because of (a) an edge shared by more than two triangles, (b) a vertex shared by two unconnected sets of triangles, and (c) a T-junction vertex.

Dual Contouring

DC improves upon the MC algorithm. DC uses the dual grid of the voxel data, locating nodes of the surface within the voxel, rather than on the edge of the voxel (as done with MC).

Boris⁴ created a figure, reproduced below, that illustrates the differences between MC and DC.

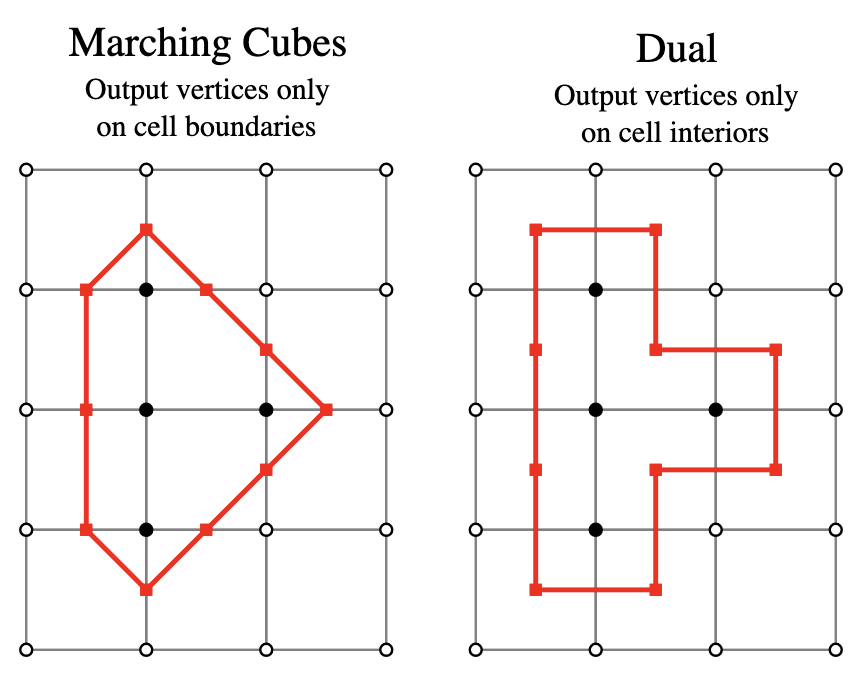
Figure: Reproduction of the figure from Boris⁴, illustrating, in two dimentions, the differences between MC and DC. White circle are outside points. Black circles are inside points. In MC, the red points indicate surface vertices at edge intersections. In DC, the red points indicate surface vertices within a voxel.

Advantages

• "[C]an produce sharp features by inserting vertices anywhere inside the grid cube, as opposed to the Marching Cubes (MC) algorithm that can insert vertices only on grid edges."⁵

Disadvantages

• More complicated than MC since DC uses both position and normal (gradient) information at voxel edges to locate the surface intersection.
• "...unable to guarantee 2-manifold and watertight meshes due to the fact that it produces only one vertex for each grid cube." "DC is that it does not guarantee 2-manifold and intersection-free surfaces. A polygonal mesh is considered as being 2-manifold if each edge of the mesh is shared by only two faces, and if the neighborhood of each vertex of the mesh is the topological equivalent of a disk." ⁵

References