Dualization
Dualization is the process of using a primal mesh to construct a dual mesh. Dualization can be performed on 2D/3D surface meshes composed of quadrilateral elements, and 3D volumetric meshes composed of hexahedral elements. Both quadrilateral and hexahedral elements will be discussed.
Quadtree
With plot_quadtree_convention.py, we create the following index scheme:
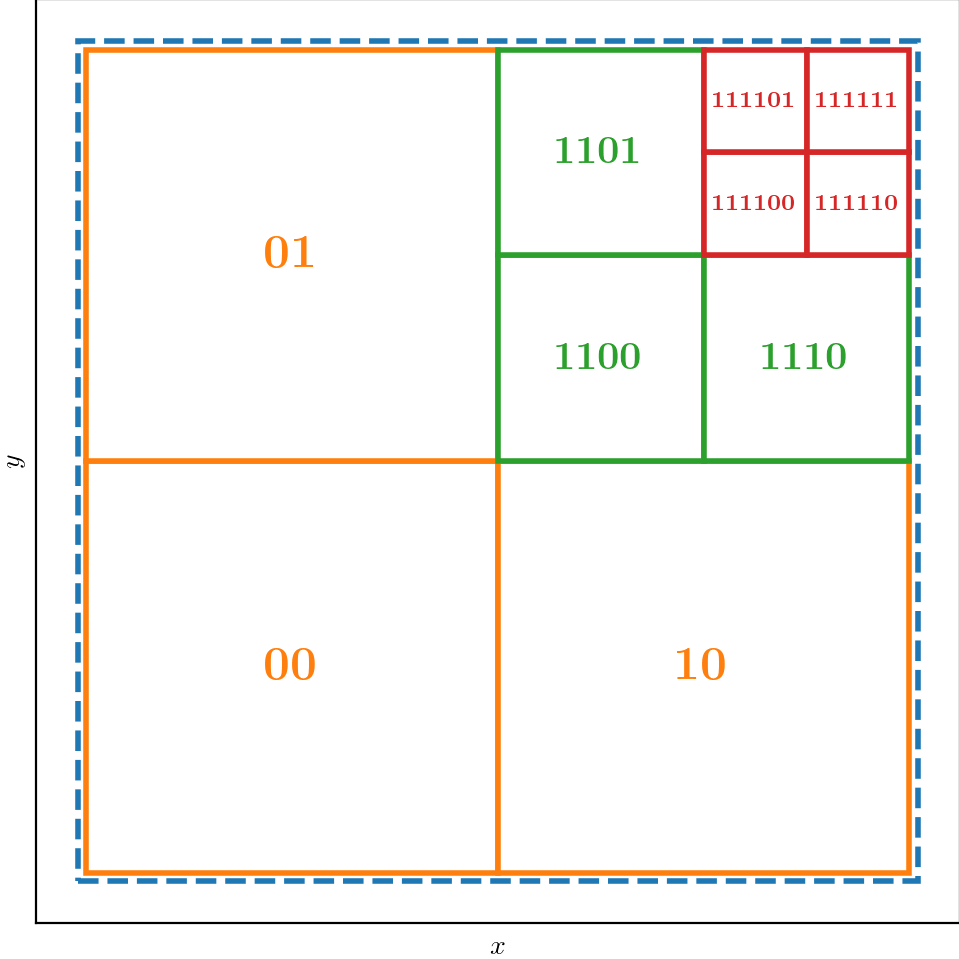
With fig_quadtree.tex, we create the following image of the inverted tree:
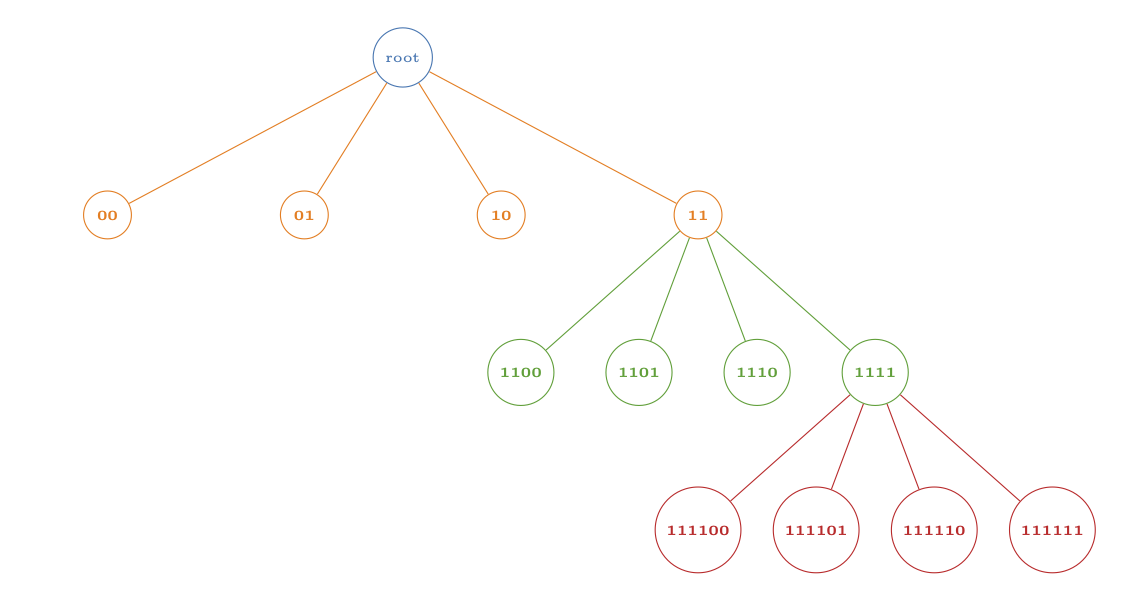
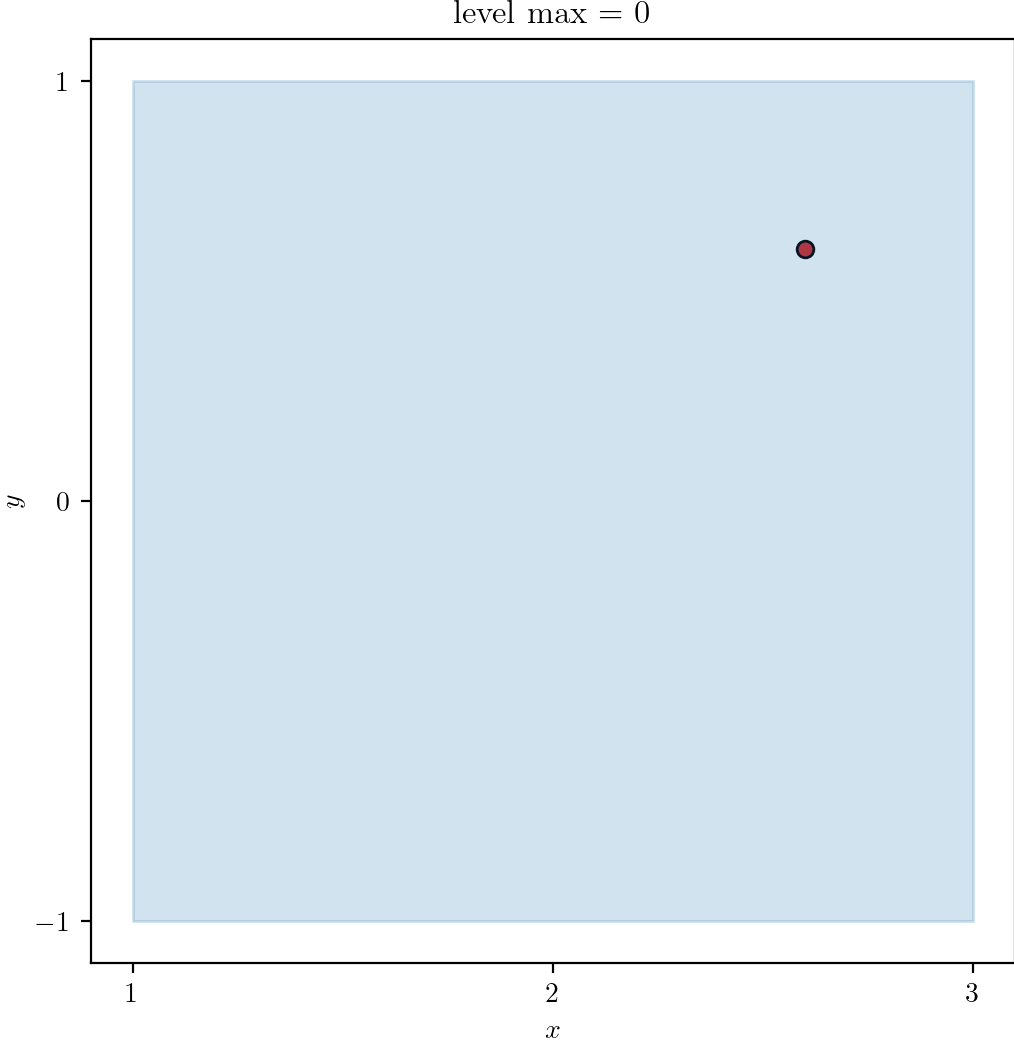
With plot_quadtree.py, we plot a domain
- A square domain
L0 - Single point at
(2.6, 0.6)to trigger refinement.
| Level 0 | 1 | 2 |
|---|---|---|
 |  |  |
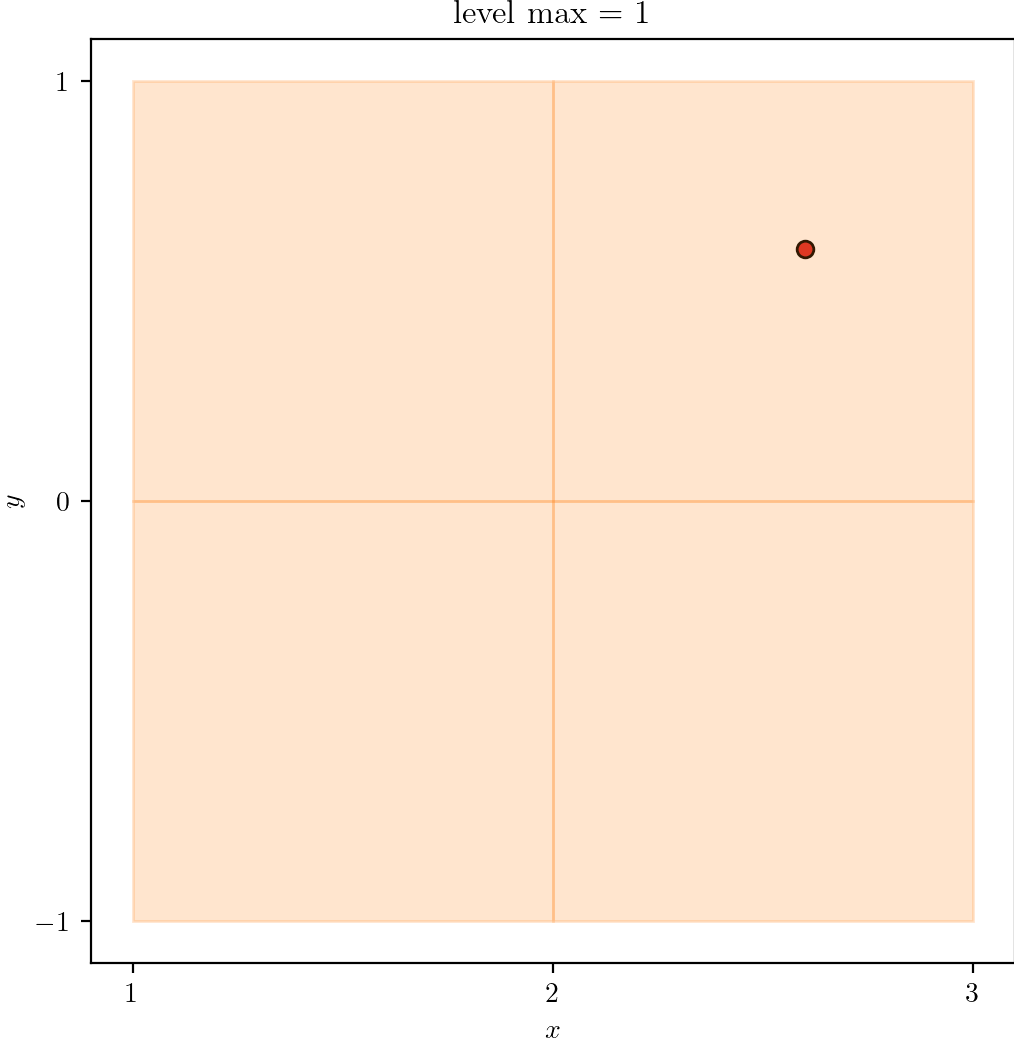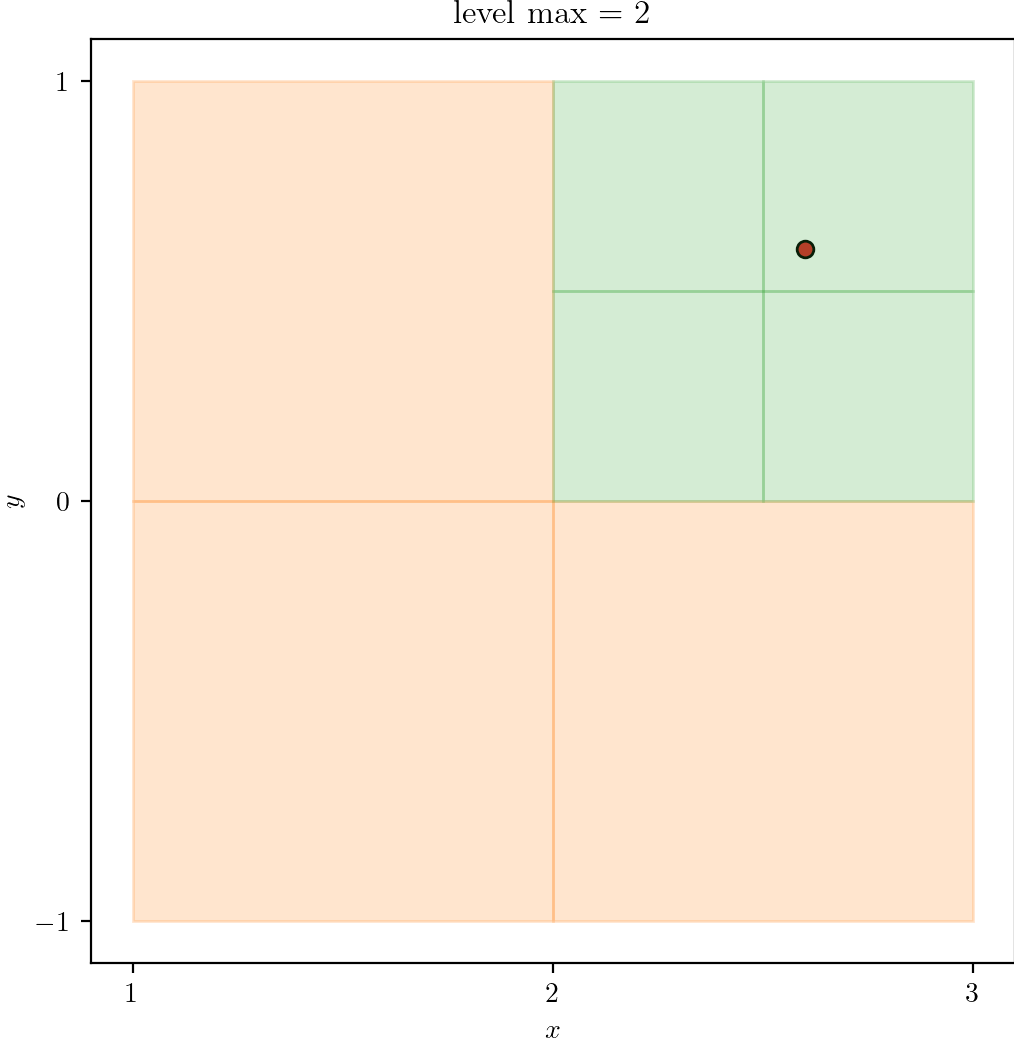| 3 | 4 | 5 |
|---|---|---|
 |  |  |
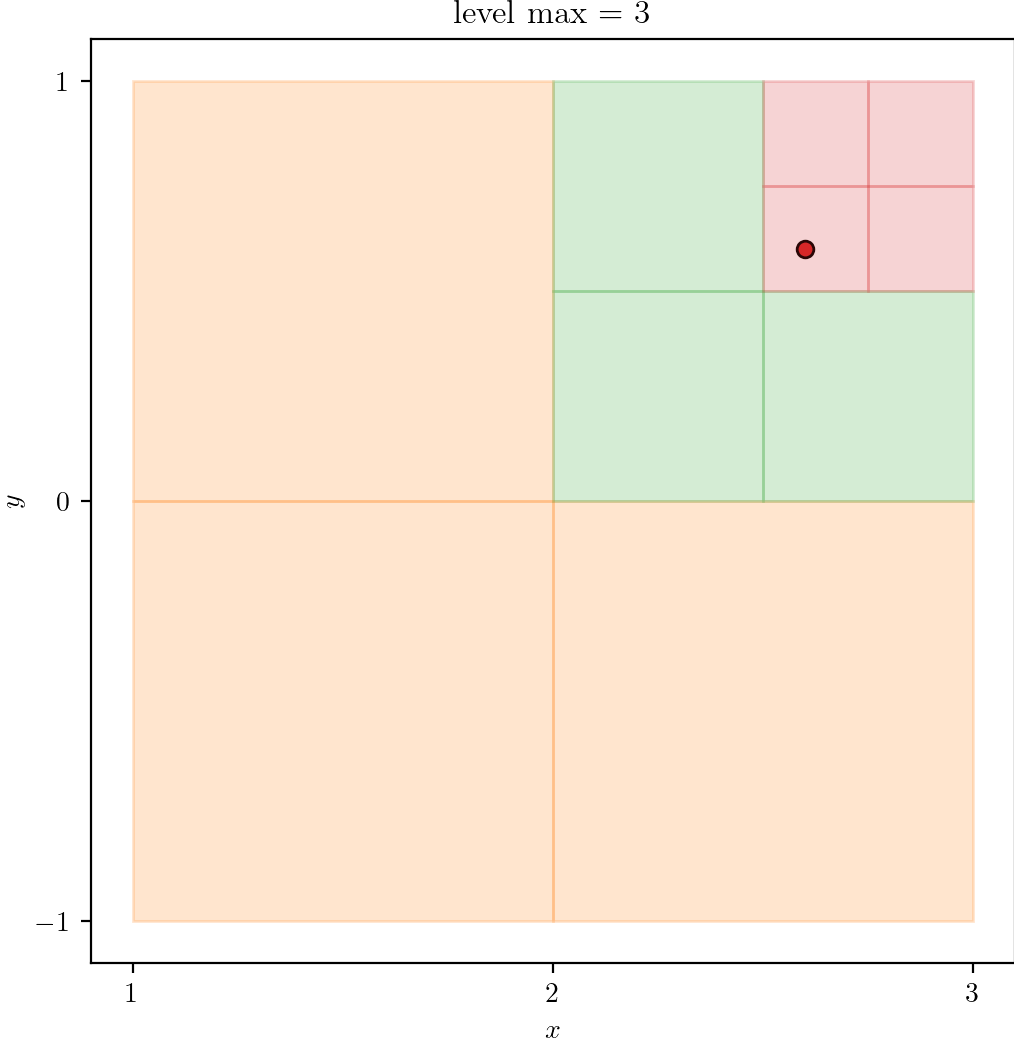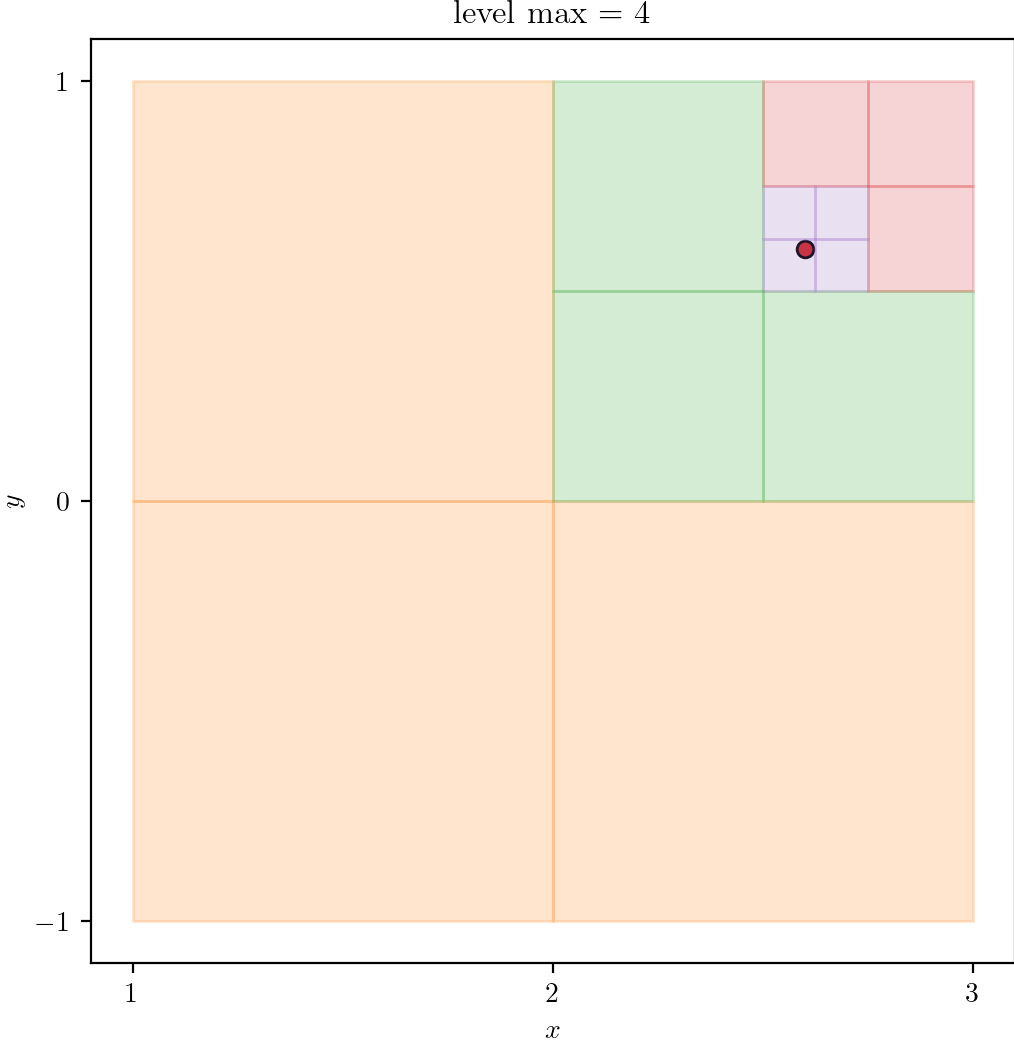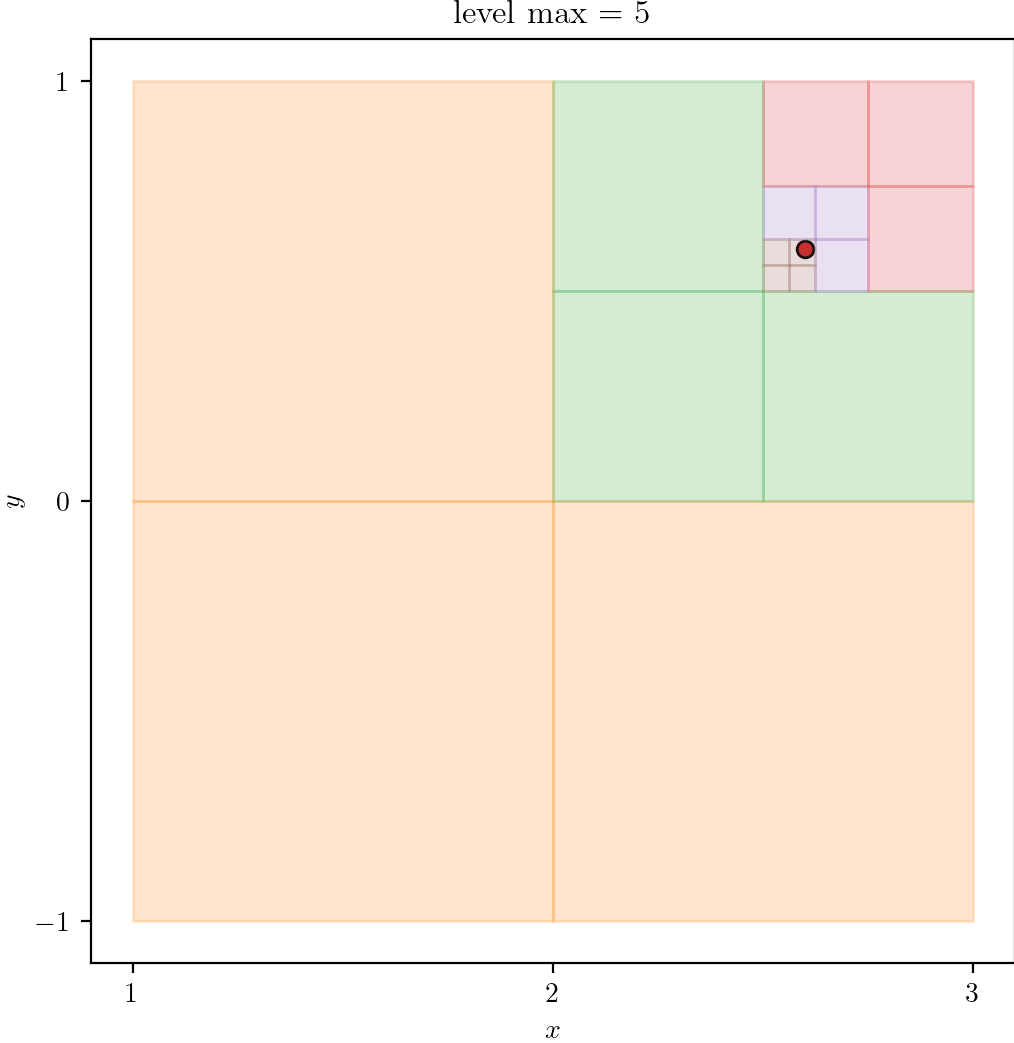Circle from Segmentation
| 3 | 4 | 5 | 6 |
|---|---|---|---|
 |  |  |  |
| 13 | 14 | 15 | 16 |
|---|---|---|---|
 |  |  |  |
Circle from Boundary
Consider a boundary of a circle defined by discrete (x, y) points.
| Level 0 | 1 | 2 |
|---|---|---|
 |  |  |
| 3 | 4 | 5 |
|---|---|---|
 |  |  |
Circle from Tesellation
Quarter Plate
With Python, we produce a Quadtree with zero to five levels of refinement. Refinement is triggered based on whether or not a cell contains one or more seed points, shown as points along the quarter circle centered at (4, 0).
| Level 0 | 1 | 2 |
|---|---|---|
 |  |  |
| 3 | 4 | 5 |
|---|---|---|
 |  |  |
Octree
Sphere
Consider a boundary of a sphere defined by a discrete triangular tesselation.
References
- https://github.com/sandialabs/sibl/blob/master/geo/doc/quadtree.md
- https://github.com/sandialabs/sibl/blob/master/geo/doc/dual_quad_transitions.md
- https://github.com/sandialabs/sibl/blob/master/geo/doc/dual/lesson_11.md
Source
quadtree_plot.py
"""This module creates a quadtree and plots it."""
from pathlib import Path
from typing import NamedTuple
import matplotlib.pyplot as plt
from matplotlib import patches
import numpy as np
# from book.dualization.code.color_schemes import QuadColors
from color_complement import ColorComplement
from color_schemes import ColorSchemes, DiscreteColors
class Point(NamedTuple):
"""A point in 2D space."""
x: float # x-coordinate
y: float # y-coordinate
class Boundary(NamedTuple):
"""A boundary defined by its minimum and maximum
x and y coordinates."""
xmin: float # Minimum x-coordinate
xmax: float # Maximum x-coordinate
ymin: float # Minimum y-coordinate
ymax: float # Maximum y-coordinate
class QuadTree:
"""Defines a quadtree composed of a single parent quad and recursive
children quads.
"""
def __init__(
self,
*,
x: float,
y: float,
width: float,
height: float,
level: int,
max_level: int,
seeds: list[Point],
verbose: bool,
):
# (x, y, width, height)
self.boundary = Boundary(xmin=x, xmax=x + width, ymin=y, ymax=y + height)
self.level = level
self.max_level = max_level
self.has_children = False
self.children = []
assert level <= max_level, (
f"QuadTree level {level} exceeds max_level {max_level}."
)
self.verbose = verbose
if self.contains_any_point(seeds):
# If the quad contains any of the seed points, subdivide it
self.subdivide(seeds=seeds)
def subdivide(self, seeds: list[Point]):
"""Divides the parent quad into four quad children."""
if self.level < self.max_level:
if self.verbose:
print(
f"Subdividing quad at level {self.level} with boundary {self.boundary}"
)
x = self.boundary.xmin
y = self.boundary.ymin
width = self.boundary.xmax - self.boundary.xmin
height = self.boundary.ymax - self.boundary.ymin
half_width = width / 2.0
half_height = height / 2.0
self.has_children = True # overwrite
# Create four children
self.children.append(
QuadTree(
x=x,
y=y,
width=half_width,
height=half_height,
level=self.level + 1,
max_level=self.max_level,
seeds=seeds,
verbose=self.verbose,
)
) # Top-left
self.children.append(
QuadTree(
x=x + half_width,
y=y,
width=half_width,
height=half_height,
level=self.level + 1,
max_level=self.max_level,
seeds=seeds,
verbose=self.verbose,
)
) # Top-right
self.children.append(
QuadTree(
x=x,
y=y + half_height,
width=half_width,
height=half_height,
level=self.level + 1,
max_level=self.max_level,
seeds=seeds,
verbose=self.verbose,
)
) # Bottom-left
self.children.append(
QuadTree(
x=x + half_width,
y=y + half_height,
width=half_width,
height=half_height,
level=self.level + 1,
max_level=self.max_level,
seeds=seeds,
verbose=self.verbose,
)
) # Bottom-right
def contains(self, point: Point) -> bool:
"""Check if the quadtree contains a point."""
# TODO: determine if we want this to be consistent with
# winding number conventions
return (
point.x >= self.boundary.xmin
and point.x <= self.boundary.xmax
and point.y >= self.boundary.ymin
and point.y <= self.boundary.ymax
)
def contains_any_point(self, points: list[Point]) -> bool:
"""Check if the quadtree contains any of the given points.
Python's built-in any() short-circuits: it returns True as
soon as it finds the first truthy value and stops evaluating the rest.
"""
# result = any(self.contains(point) for point in points)
# return result
return any(self.contains(point) for point in points)
def draw(self, ax, quadcolors: DiscreteColors, seeds: list[Point] | None):
"""Draw the quadtree."""
x = self.boundary.xmin
y = self.boundary.ymin
width = self.boundary.xmax - self.boundary.xmin
height = self.boundary.ymax - self.boundary.ymin
# Draw the boundary rectangle
if self.verbose:
print(
f"Drawing level {self.level} quad at ({x}, {y}) with width {width} and height {height}"
)
rect = patches.Rectangle(
(x, y),
width,
height,
# linewidth=1,
linestyle="solid",
edgecolor=quadcolors.edgecolor,
# facecolor=ColorComplement.hex_complement(
# quadcolors.facecolors[self.level], "hsv"
# ),
facecolor=quadcolors.facecolors[self.level],
alpha=quadcolors.alpha,
zorder=2,
)
ax.add_patch(rect)
# Draw children
if self.has_children:
if self.verbose:
print(f"Quad at level {self.level} has children, drawing them.")
for child in self.children:
child.draw(ax, quadcolors, seeds)
# Draw the seed points, only draw them after we have reached
# the top level of the quadtree to avoid cluttering the plot
# with too many points at lower levels.
if seeds is not None and self.level == self.max_level:
xs = [seed.x for seed in seeds]
ys = [seed.y for seed in seeds]
ax.scatter(
xs,
ys,
marker="o",
edgecolor=quadcolors.edgecolor,
color=ColorComplement.hex_complement(
quadcolors.facecolors[self.level], "hsv"
),
alpha=quadcolors.alpha,
s=20, # Adjust size as needed
zorder=3,
)
class Configuration(NamedTuple):
"""User input configuration for the quadtree plot."""
xmin: float # Minimum x-coordinate for the quadtree
xmax: float # Maximum x-coordinate for the quadtree
ymin: float # Minimum y-coordinate for the quadtree
ymax: float # Maximum y-coordinate for the quadtree
level_min: int # Minimum level of the quadtree
level_max: int # Maximum level of the quadtree
seeds: list[Point] # List of seed points for the quadtree
fig_stem: str # Stem for the filename when saving
alpha: float = 1.0 # Transparency of the quadtree colors
save: bool = True # Whether to save the plot
show: bool = True # Whether to show the plot
dpi: int = 300 # Dots per inch for saving the plot
fig_width: float = 6.0 # Width of the figure in inches
fig_height: float = 6.0 # Height of the figure in inches
ext: str = ".svg" # File extension for saving the plot
verbose: bool = False # Whether to print debug information
def quarter_plate_seeds() -> list[Point]:
"""Helper function to create seeds for the Hughes quarter plate example."""
# Similar to the round in the Hughes quarter plate problem
# https://github.com/sandialabs/sibl/blob/master/geo/doc/dual/lesson_11.md
# see also Cottrell 2009 IGA book, page 117.
radius = 1.0
theta_start = np.pi / 2.0
theta_stop = np.pi
n_points = 9
theta_values = np.linspace(theta_start, theta_stop, n_points)
offset_x, offset_y = 4.0, 0.0
seeds = [
Point(x=radius * np.cos(theta) + offset_x, y=radius * np.sin(theta) + offset_y)
for theta in theta_values
]
corner_seeds = [
Point(x=4, y=4),
Point(x=0, y=4),
Point(x=0, y=0),
]
seeds += corner_seeds
return seeds
def circle_seeds() -> list[Point]:
"""Helper function to create seeds for a circle."""
# Create an array of angles from 0 to 2 pi
center = (0, 0)
radius = 50
n_pts = 36
theta = np.linspace(0, 2 * np.pi, n_pts + 1)
# Parametric equations for the circle
x = center[0] + radius * np.cos(theta)
y = center[1] + radius * np.sin(theta)
seeds = [Point(x=xi, y=yi) for xi, yi in zip(x, y)]
return seeds
def main():
# Circle example
cc = Configuration(
xmin=-60,
xmax=60,
ymin=-60,
ymax=60,
#
level_min=0,
level_max=5,
#
seeds=circle_seeds(),
#
fig_stem="quadtree_circle",
)
# Hughes quarter plate example
_cc = Configuration(
xmin=-2,
xmax=6,
ymin=-2,
ymax=6,
#
level_min=0,
level_max=4,
#
seeds=quarter_plate_seeds(),
#
fig_stem="quadtree_quarter_plate",
)
# Create a figure and axis
fig, ax = plt.subplots(figsize=(cc.fig_width, cc.fig_height))
# Create the quadtree with a boundary of (-12, -12, 24, 24)
qt = QuadTree(
x=cc.xmin,
y=cc.ymin,
width=cc.xmax - cc.xmin,
height=cc.ymax - cc.ymin,
level=cc.level_min,
max_level=cc.level_max,
verbose=cc.verbose,
seeds=cc.seeds,
)
# The number of colors will be the number of levels + 1 because
# the root level is 0 and we want to include it in the color palette
# n_colors = level_max - level_min + 2
n_colors = 10 # Number of discrete colors to extract
qc = DiscreteColors(
n_levels=n_colors,
edgecolor="black",
alpha=cc.alpha,
color_scheme=ColorSchemes.TAB10,
reversed=False,
)
if cc.verbose:
print(f"quadcolors.facecolors: {qc.facecolors}")
# Draw the quadtree
qt.draw(ax=ax, quadcolors=qc, seeds=cc.seeds)
# Set limits and aspect
margin = 0.1 * (cc.xmax - cc.xmin)
ax.set_xlim(cc.xmin - margin, cc.xmax + margin)
ax.set_ylim(cc.ymin - margin, cc.ymax + margin)
ax.set_aspect("equal")
ax.set_xlabel("x")
ax.set_ylabel("y")
# Turn grid to off
ax.grid(False)
# ax.set_xticks([])
# ax.set_yticks([])
GRAMMAR_LEVELS = (
f"{cc.level_max} Level" if cc.level_max == 1 else f"{cc.level_max} Levels"
)
ax.set_title(f"Quadtree with {GRAMMAR_LEVELS} of Refinement")
plt.show()
if cc.show:
plt.show()
if cc.save:
parent = Path(__file__).parent
# stem = Path(__file__).stem + "_level_" + str(cc.level_max)
stem = cc.fig_stem + "_level_" + str(cc.level_max)
fn = parent.joinpath(stem + cc.ext)
# plt.savefig(fn, dpi=DPI, bbox_inches='tight')
fig.savefig(fn, dpi=cc.dpi)
print(f"Saved {fn}")
if __name__ == "__main__":
main()