Spheres
We segment a sphere into very coarse voxel meshes. The Python code used to generate the voxelations and figures is included below.
Segmentation
Objective: Create very coarse spheres of three successively more refined
resolutions, radius=1, radius=3, and radius=5, as shown below:
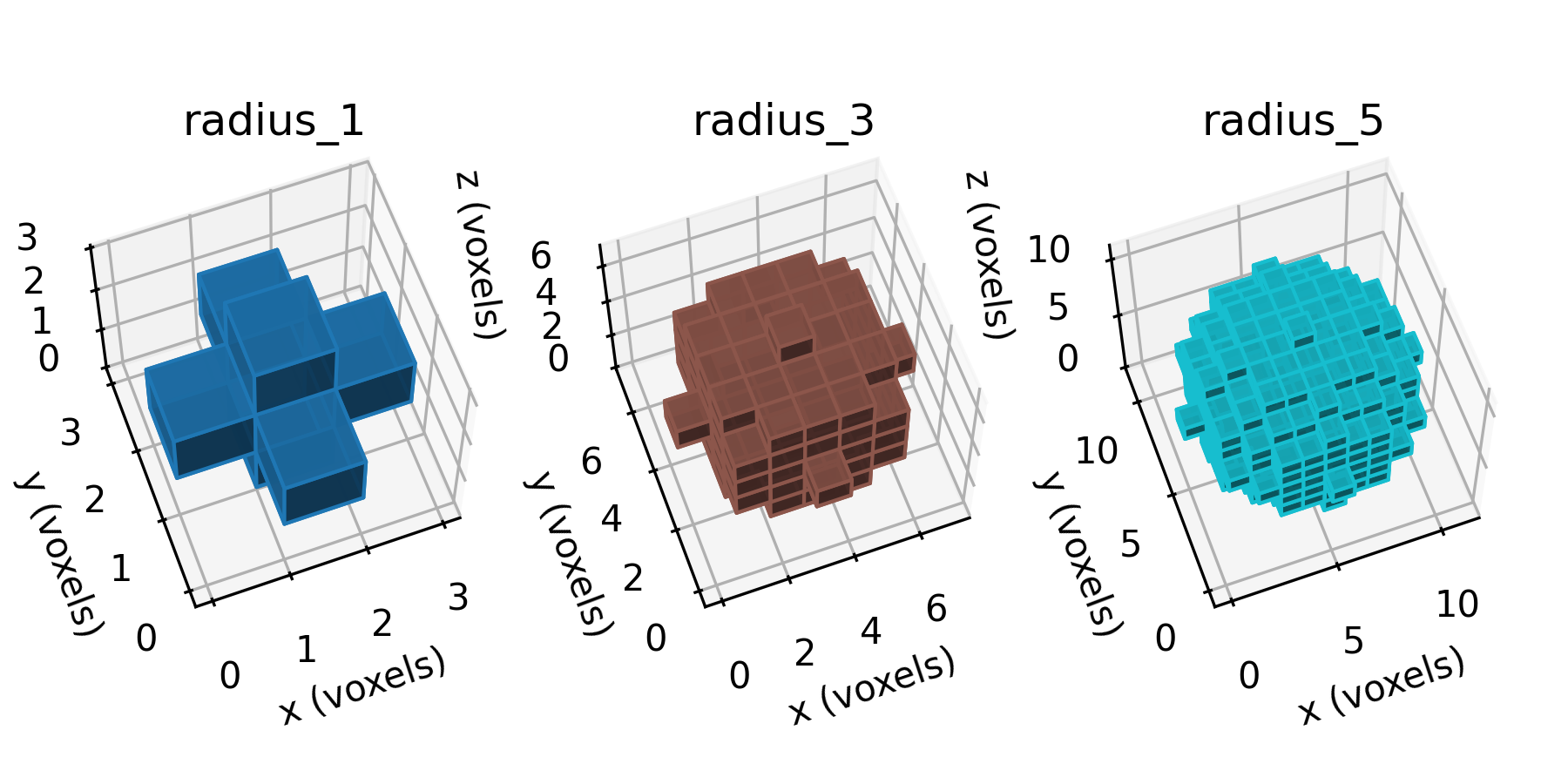
Figure: Sphere segmentations at selected resolutions, shown in the voxel domain.
The radius=1 case has the following data structure,
spheres["radius_1"]
array([[[0, 0, 0],
[0, 1, 0],
[0, 0, 0]],
[[0, 1, 0],
[1, 1, 1],
[0, 1, 0]],
[[0, 0, 0],
[0, 1, 0],
[0, 0, 0]]], dtype=uint8)
Because of large size, the data structures for sphere_3 and
sphere_5 are not shown here.
These segmentations are saved to
automesh
automesh is used to convert the .npy segmentations into .inp meshes.
automesh mesh hex -i spheres_radius_1.npy -o spheres_radius_1.inp
automesh 0.3.7
Reading spheres_radius_1.npy
Done 79.219µs [2 materials, 27 voxels]
Meshing voxels into hexahedra
Done 294.934µs [2 blocks, 27 elements, 64 nodes]
Writing spheres_radius_1.inp
Done 111.51µs
Total 883.068µs
automesh mesh hex -i spheres_radius_3.npy -o spheres_radius_3.inp
automesh 0.3.7
Reading spheres_radius_3.npy
Done 73.127µs [2 materials, 343 voxels]
Meshing voxels into hexahedra
Done 353.304µs [2 blocks, 343 elements, 512 nodes]
Writing spheres_radius_3.inp
Done 698.068µs
Total 1.478624ms
automesh mesh hex -i spheres_radius_5.npy -o spheres_radius_5.inp
automesh 0.3.7
Reading spheres_radius_5.npy
Done 77.255µs [2 materials, 1331 voxels]
Meshing voxels into hexahedra
Done 593.905µs [2 blocks, 1331 elements, 1728 nodes]
Writing spheres_radius_5.inp
Done 2.179974ms
Total 3.204698ms
Mesh
The spheres_radius_1.inp file:
** autotwin.automesh
** version 0.3.7
** autogenerated on 2025-12-10 19:08:02.559623687 UTC
********************************** N O D E S **********************************
*NODE, NSET=ALLNODES
1, 0.000000e0, 0.000000e0, 0.000000e0
2, 1.000000e0, 0.000000e0, 0.000000e0
3, 2.000000e0, 0.000000e0, 0.000000e0
4, 3.000000e0, 0.000000e0, 0.000000e0
5, 0.000000e0, 1.000000e0, 0.000000e0
6, 1.000000e0, 1.000000e0, 0.000000e0
7, 2.000000e0, 1.000000e0, 0.000000e0
8, 3.000000e0, 1.000000e0, 0.000000e0
9, 0.000000e0, 2.000000e0, 0.000000e0
10, 1.000000e0, 2.000000e0, 0.000000e0
11, 2.000000e0, 2.000000e0, 0.000000e0
12, 3.000000e0, 2.000000e0, 0.000000e0
13, 0.000000e0, 3.000000e0, 0.000000e0
14, 1.000000e0, 3.000000e0, 0.000000e0
15, 2.000000e0, 3.000000e0, 0.000000e0
16, 3.000000e0, 3.000000e0, 0.000000e0
17, 0.000000e0, 0.000000e0, 1.000000e0
18, 1.000000e0, 0.000000e0, 1.000000e0
19, 2.000000e0, 0.000000e0, 1.000000e0
20, 3.000000e0, 0.000000e0, 1.000000e0
21, 0.000000e0, 1.000000e0, 1.000000e0
22, 1.000000e0, 1.000000e0, 1.000000e0
23, 2.000000e0, 1.000000e0, 1.000000e0
24, 3.000000e0, 1.000000e0, 1.000000e0
25, 0.000000e0, 2.000000e0, 1.000000e0
26, 1.000000e0, 2.000000e0, 1.000000e0
27, 2.000000e0, 2.000000e0, 1.000000e0
28, 3.000000e0, 2.000000e0, 1.000000e0
29, 0.000000e0, 3.000000e0, 1.000000e0
30, 1.000000e0, 3.000000e0, 1.000000e0
31, 2.000000e0, 3.000000e0, 1.000000e0
32, 3.000000e0, 3.000000e0, 1.000000e0
33, 0.000000e0, 0.000000e0, 2.000000e0
34, 1.000000e0, 0.000000e0, 2.000000e0
35, 2.000000e0, 0.000000e0, 2.000000e0
36, 3.000000e0, 0.000000e0, 2.000000e0
37, 0.000000e0, 1.000000e0, 2.000000e0
38, 1.000000e0, 1.000000e0, 2.000000e0
39, 2.000000e0, 1.000000e0, 2.000000e0
40, 3.000000e0, 1.000000e0, 2.000000e0
41, 0.000000e0, 2.000000e0, 2.000000e0
42, 1.000000e0, 2.000000e0, 2.000000e0
43, 2.000000e0, 2.000000e0, 2.000000e0
44, 3.000000e0, 2.000000e0, 2.000000e0
45, 0.000000e0, 3.000000e0, 2.000000e0
46, 1.000000e0, 3.000000e0, 2.000000e0
47, 2.000000e0, 3.000000e0, 2.000000e0
48, 3.000000e0, 3.000000e0, 2.000000e0
49, 0.000000e0, 0.000000e0, 3.000000e0
50, 1.000000e0, 0.000000e0, 3.000000e0
51, 2.000000e0, 0.000000e0, 3.000000e0
52, 3.000000e0, 0.000000e0, 3.000000e0
53, 0.000000e0, 1.000000e0, 3.000000e0
54, 1.000000e0, 1.000000e0, 3.000000e0
55, 2.000000e0, 1.000000e0, 3.000000e0
56, 3.000000e0, 1.000000e0, 3.000000e0
57, 0.000000e0, 2.000000e0, 3.000000e0
58, 1.000000e0, 2.000000e0, 3.000000e0
59, 2.000000e0, 2.000000e0, 3.000000e0
60, 3.000000e0, 2.000000e0, 3.000000e0
61, 0.000000e0, 3.000000e0, 3.000000e0
62, 1.000000e0, 3.000000e0, 3.000000e0
63, 2.000000e0, 3.000000e0, 3.000000e0
64, 3.000000e0, 3.000000e0, 3.000000e0
**
********************************** E L E M E N T S ****************************
*ELEMENT, TYPE=C3D8R, ELSET=EB0
1, 1, 2, 6, 5, 17, 18, 22, 21
2, 2, 3, 7, 6, 18, 19, 23, 22
3, 3, 4, 8, 7, 19, 20, 24, 23
4, 5, 6, 10, 9, 21, 22, 26, 25
6, 7, 8, 12, 11, 23, 24, 28, 27
7, 9, 10, 14, 13, 25, 26, 30, 29
8, 10, 11, 15, 14, 26, 27, 31, 30
9, 11, 12, 16, 15, 27, 28, 32, 31
10, 17, 18, 22, 21, 33, 34, 38, 37
12, 19, 20, 24, 23, 35, 36, 40, 39
16, 25, 26, 30, 29, 41, 42, 46, 45
18, 27, 28, 32, 31, 43, 44, 48, 47
19, 33, 34, 38, 37, 49, 50, 54, 53
20, 34, 35, 39, 38, 50, 51, 55, 54
21, 35, 36, 40, 39, 51, 52, 56, 55
22, 37, 38, 42, 41, 53, 54, 58, 57
24, 39, 40, 44, 43, 55, 56, 60, 59
25, 41, 42, 46, 45, 57, 58, 62, 61
26, 42, 43, 47, 46, 58, 59, 63, 62
27, 43, 44, 48, 47, 59, 60, 64, 63
*ELEMENT, TYPE=C3D8R, ELSET=EB1
5, 6, 7, 11, 10, 22, 23, 27, 26
11, 18, 19, 23, 22, 34, 35, 39, 38
13, 21, 22, 26, 25, 37, 38, 42, 41
14, 22, 23, 27, 26, 38, 39, 43, 42
15, 23, 24, 28, 27, 39, 40, 44, 43
17, 26, 27, 31, 30, 42, 43, 47, 46
23, 38, 39, 43, 42, 54, 55, 59, 58
**```
Because of large size, the mesh structures for `sphere_3` and
`sphere_5` are not shown here.
## Source
### `spheres.py`
```python
r"""This module, spheres.py, creates a voxelized sphere and exports
it as a .npy file.
Example
-------
source ~/autotwin/automesh/.venv/bin/activate
cd book/examples/spheres
python spheres.py
"""
from pathlib import Path
from typing import Final
from matplotlib.colors import LightSource
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
def sphere(radius: int, dtype=np.uint8) -> np.ndarray:
"""Generate a 3D voxelized representation of a sphere.
Parameters
----------
radius: int
The radius of the sphere. Minimum value is 1.
dtype: data-type, optional
The data type of the output array. Default is np.uint8.
Returns
-------
np.ndarray
A 3D numpy array of shape (2*radius+1, 2*radius+1, 2*radius+1)
representing the voxelized sphere. Voxels within the sphere are
set to 1, and those outside are set to 0.
Raises
------
ValueError
If the radius is less than 1.
Example
-------
>>> sphere(radius=1) returns
array(
[
[[0, 0, 0], [0, 1, 0], [0, 0, 0]],
[[0, 1, 0], [1, 1, 1], [0, 1, 0]],
[[0, 0, 0], [0, 1, 0], [0, 0, 0]]
],
dtype=uint8
)
Reference
---------
Adapted from:
https://github.com/scikit-image/scikit-image/blob/v0.24.0/skimage/morphology/footprints.py#L763-L833
"""
if radius < 1:
raise ValueError("Radius must be >= 1")
n_voxels_per_side = 2 * radius + 1
vox_z, vox_y, vox_x = np.mgrid[
-radius : radius : n_voxels_per_side * 1j,
-radius : radius : n_voxels_per_side * 1j,
-radius : radius : n_voxels_per_side * 1j,
]
voxel_radius_squared = vox_x**2 + vox_y**2 + vox_z**2
result = np.array(voxel_radius_squared <= radius * radius, dtype=dtype)
return result
# User input begin
spheres = {
"radius_1": sphere(radius=1),
"radius_3": sphere(radius=3),
"radius_5": sphere(radius=5),
}
aa = Path(__file__)
bb = aa.with_suffix(".png")
# Visualize the elements.
width, height = 10, 5
# width, height = 8, 4
# width, height = 6, 3
fig = plt.figure(figsize=(width, height))
el, az, roll = 63, -110, 0
cmap = plt.get_cmap(name="tab10")
# NUM_COLORS = len(spheres)
NUM_COLORS = 10 # consistent with tab10 color scheme
VOXEL_ALPHA: Final[float] = 0.9
colors = cmap(np.linspace(0, 1, NUM_COLORS))
lightsource = LightSource(azdeg=325, altdeg=45) # azimuth, elevation
# lightsource = LightSource(azdeg=325, altdeg=90) # azimuth, elevation
DPI: Final[int] = 300 # resolution, dots per inch
SHOW: Final[bool] = False # turn to True to show the figure on screen
SAVE: Final[bool] = False # turn to True to save .png and .npy files
# User input end
N_SUBPLOTS = len(spheres)
IDX = 1
for index, (key, value) in enumerate(spheres.items()):
ax = fig.add_subplot(1, N_SUBPLOTS, index + 1, projection=Axes3D.name)
ax.voxels(
value,
facecolors=colors[index],
edgecolor=colors[index],
alpha=VOXEL_ALPHA,
lightsource=lightsource,
)
ax.set_title(key.replace("_", "="))
IDX += 1
# Set labels for the axes
ax.set_xlabel("x (voxels)")
ax.set_ylabel("y (voxels)")
ax.set_zlabel("z (voxels)")
# Set the camera view
ax.set_aspect("equal")
ax.view_init(elev=el, azim=az, roll=roll)
if SAVE:
cc = aa.with_stem("spheres_" + key)
dd = cc.with_suffix(".npy")
# Save the data in .npy format
np.save(dd, value)
print(f"Saved: {dd}")
fig.tight_layout()
if SHOW:
plt.show()
if SAVE:
fig.savefig(bb, dpi=DPI)
print(f"Saved: {bb}")
test_spheres.py
r"""This module, test_spheres.py, performs point testing of the sphere module.
Example
-------
source ~/autotwin/automesh/.venv/bin/activate
python -m pytest book/examples/spheres/test_spheres.py
"""
import numpy as np
import pytest
import spheres as sph
def test_sphere():
"""Unit tests for the sphere function."""
# Assure that radius >=1 assert is raised
with pytest.raises(ValueError, match="Radius must be >= 1"):
sph.sphere(radius=0)
# Assure radius=1 is correct
gold_r1 = np.array(
[
[[0, 0, 0], [0, 1, 0], [0, 0, 0]],
[[0, 1, 0], [1, 1, 1], [0, 1, 0]],
[[0, 0, 0], [0, 1, 0], [0, 0, 0]],
],
dtype=np.uint8,
)
result_r1 = sph.sphere(radius=1)
assert np.all(gold_r1 == result_r1)
# Assure radius=2 is correct
gold_r2 = np.array(
[
[
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 1, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
],
[
[0, 0, 0, 0, 0],
[0, 1, 1, 1, 0],
[0, 1, 1, 1, 0],
[0, 1, 1, 1, 0],
[0, 0, 0, 0, 0],
],
[
[0, 0, 1, 0, 0],
[0, 1, 1, 1, 0],
[1, 1, 1, 1, 1],
[0, 1, 1, 1, 0],
[0, 0, 1, 0, 0],
],
[
[0, 0, 0, 0, 0],
[0, 1, 1, 1, 0],
[0, 1, 1, 1, 0],
[0, 1, 1, 1, 0],
[0, 0, 0, 0, 0],
],
[
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 1, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
],
],
dtype=np.uint8,
)
result_r2 = sph.sphere(radius=2)
assert np.all(gold_r2 == result_r2)
# Assure radius=3 is correct
gold_r3 = np.array(
[
[
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 1, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
],
[
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 1, 1, 1, 0, 0],
[0, 1, 1, 1, 1, 1, 0],
[0, 1, 1, 1, 1, 1, 0],
[0, 1, 1, 1, 1, 1, 0],
[0, 0, 1, 1, 1, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
],
[
[0, 0, 0, 0, 0, 0, 0],
[0, 1, 1, 1, 1, 1, 0],
[0, 1, 1, 1, 1, 1, 0],
[0, 1, 1, 1, 1, 1, 0],
[0, 1, 1, 1, 1, 1, 0],
[0, 1, 1, 1, 1, 1, 0],
[0, 0, 0, 0, 0, 0, 0],
],
[
[0, 0, 0, 1, 0, 0, 0],
[0, 1, 1, 1, 1, 1, 0],
[0, 1, 1, 1, 1, 1, 0],
[1, 1, 1, 1, 1, 1, 1],
[0, 1, 1, 1, 1, 1, 0],
[0, 1, 1, 1, 1, 1, 0],
[0, 0, 0, 1, 0, 0, 0],
],
[
[0, 0, 0, 0, 0, 0, 0],
[0, 1, 1, 1, 1, 1, 0],
[0, 1, 1, 1, 1, 1, 0],
[0, 1, 1, 1, 1, 1, 0],
[0, 1, 1, 1, 1, 1, 0],
[0, 1, 1, 1, 1, 1, 0],
[0, 0, 0, 0, 0, 0, 0],
],
[
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 1, 1, 1, 0, 0],
[0, 1, 1, 1, 1, 1, 0],
[0, 1, 1, 1, 1, 1, 0],
[0, 1, 1, 1, 1, 1, 0],
[0, 0, 1, 1, 1, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
],
[
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 1, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
],
],
dtype=np.uint8,
)
result_r3 = sph.sphere(radius=3)
assert np.all(gold_r3 == result_r3)