Unit Tests
The following illustates a subset of the unit tests used to validate the code implementation. For a complete listing of the unit sets, see voxels.rs and voxel.py.
The Python code used to generate the figures is included below.
Remark: We use the convention np when importing numpy as follows:
import numpy as np
Single
The minimum working example (MWE) is a single voxel, used to create a single mesh consisting of one block consisting of a single element. The NumPy input single.npy contains the following segmentation:
segmentation = np.array(
[
[
[ 11, ],
],
],
dtype=np.uint8,
)
where the segmentation 11 denotes block 11 in the finite element mesh.
Remark: Serialization (write and read)
| Write | Read |
|---|---|
Use the np.save command to serialize the segmentation a .npy file | Use the np.load command to deserialize the segmentation from a .npy file |
Example: Write the data in segmentation to a file called seg.npynp.save("seg.npy", segmentation) | Example: Read the data from the file seg.npy to a variable called loaded_arrayloaded_array = np.load("seg.npy") |
Equivalently, the single.spn contains a single integer:
11 # x:1 y:1 z:1
The resulting finite element mesh is visualized is shown in the following figure:
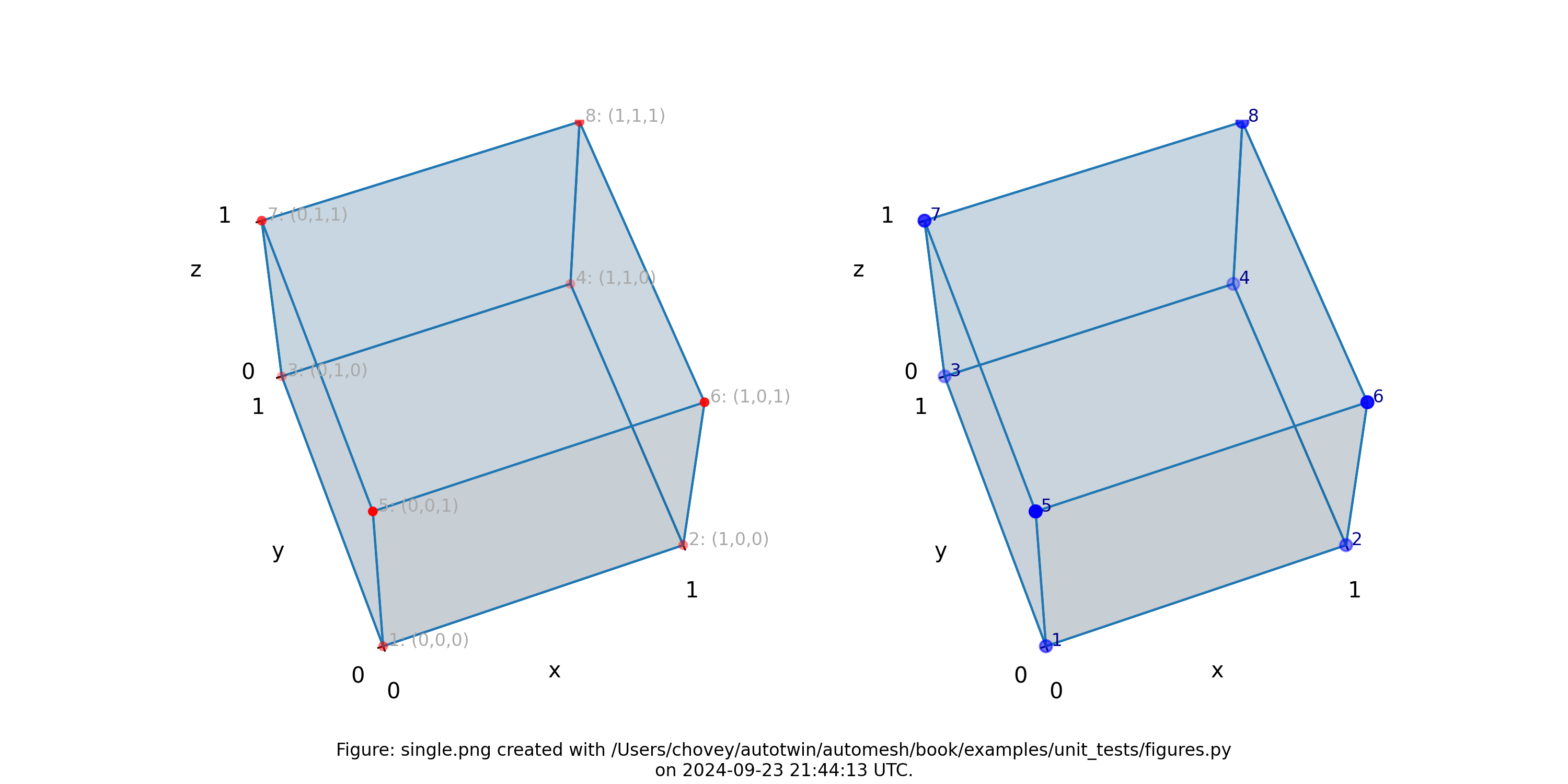
Figure: The single.png visualization, (left) lattice node numbers, (right)
mesh node numbers. Lattice node numbers appear in gray, with (x, y, z)
indices in parenthesis. The right-hand rule is used. Lattice coordinates
start at (0, 0, 0), and proceed along the x-axis, then
the y-axis, and then the z-axis.
The finite element mesh local node numbering map to the following global node numbers identically, and :
[1, 2, 4, 3, 5, 6, 8, 7]
->
[1, 2, 4, 3, 5, 6, 8, 7]
which is a special case not typically observed, as shown in more complex examples below.
Remark: Input .npy and .spn files for the examples below can be found on the repository at tests/input.
Double
The next level of complexity example is a two-voxel domain, used to create
a single block composed of two finite elements. We test propagation in
both the x and y directions. The figures below show these two
meshes.
Double X
11 # x:1 y:1 z:1
11 # 2 1 1
where the segmentation 11 denotes block 11 in the finite element mesh.
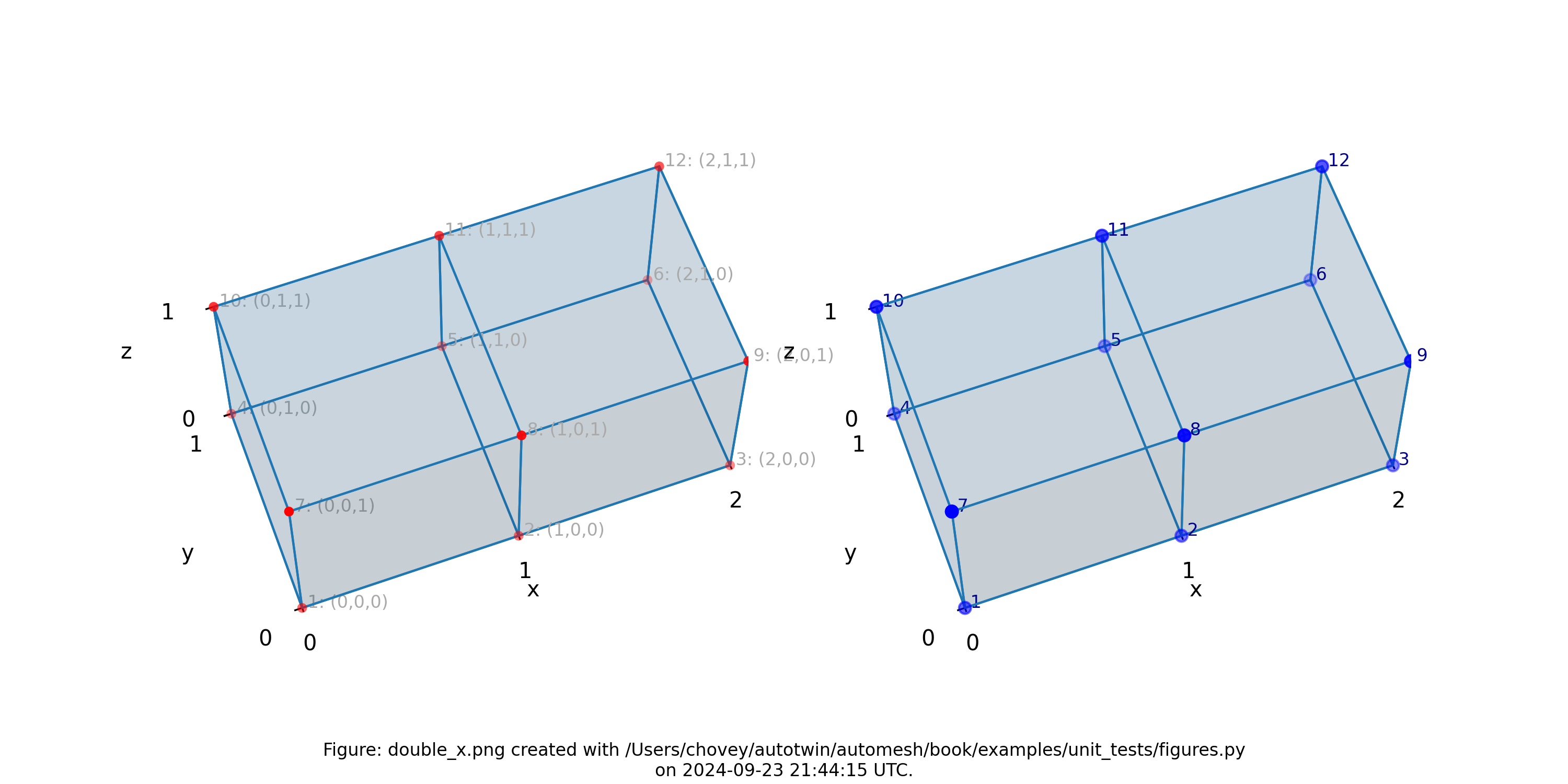
Figure: Mesh composed of a single block with two elements, propagating along
the x-axis, (left) lattice node numbers, (right) mesh node numbers.
Double Y
11 # x:1 y:1 z:1
11 # 1 2 1
where the segmentation 11 denotes block 11 in the finite element mesh.
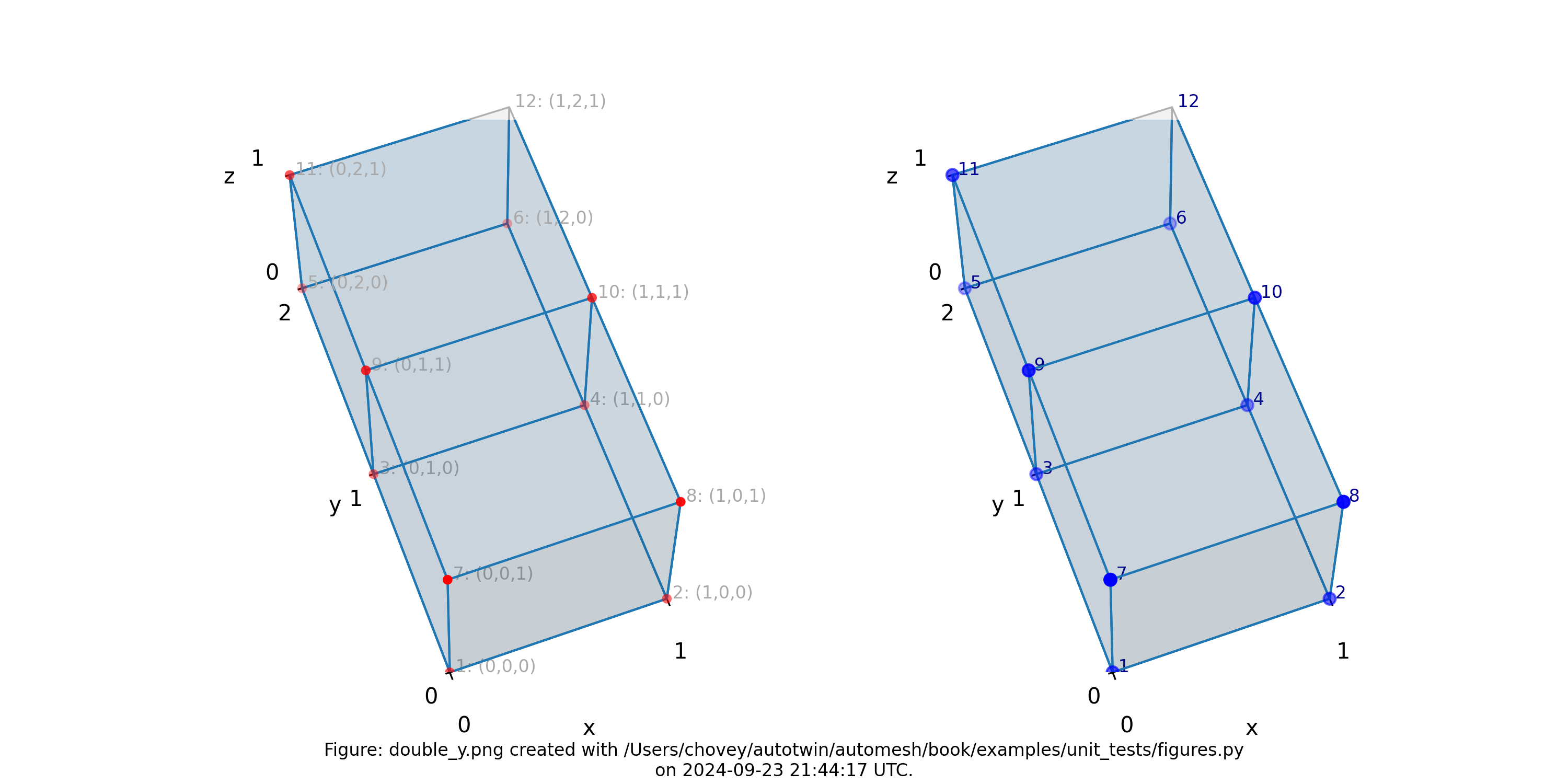
Figure: Mesh composed of a single block with two elements, propagating along
the y-axis, (left) lattice node numbers, (right) mesh node numbers.
Triple
11 # x:1 y:1 z:1
11 # 2 1 1
11 # 3 1 1
where the segmentation 11 denotes block 11 in the finite element mesh.
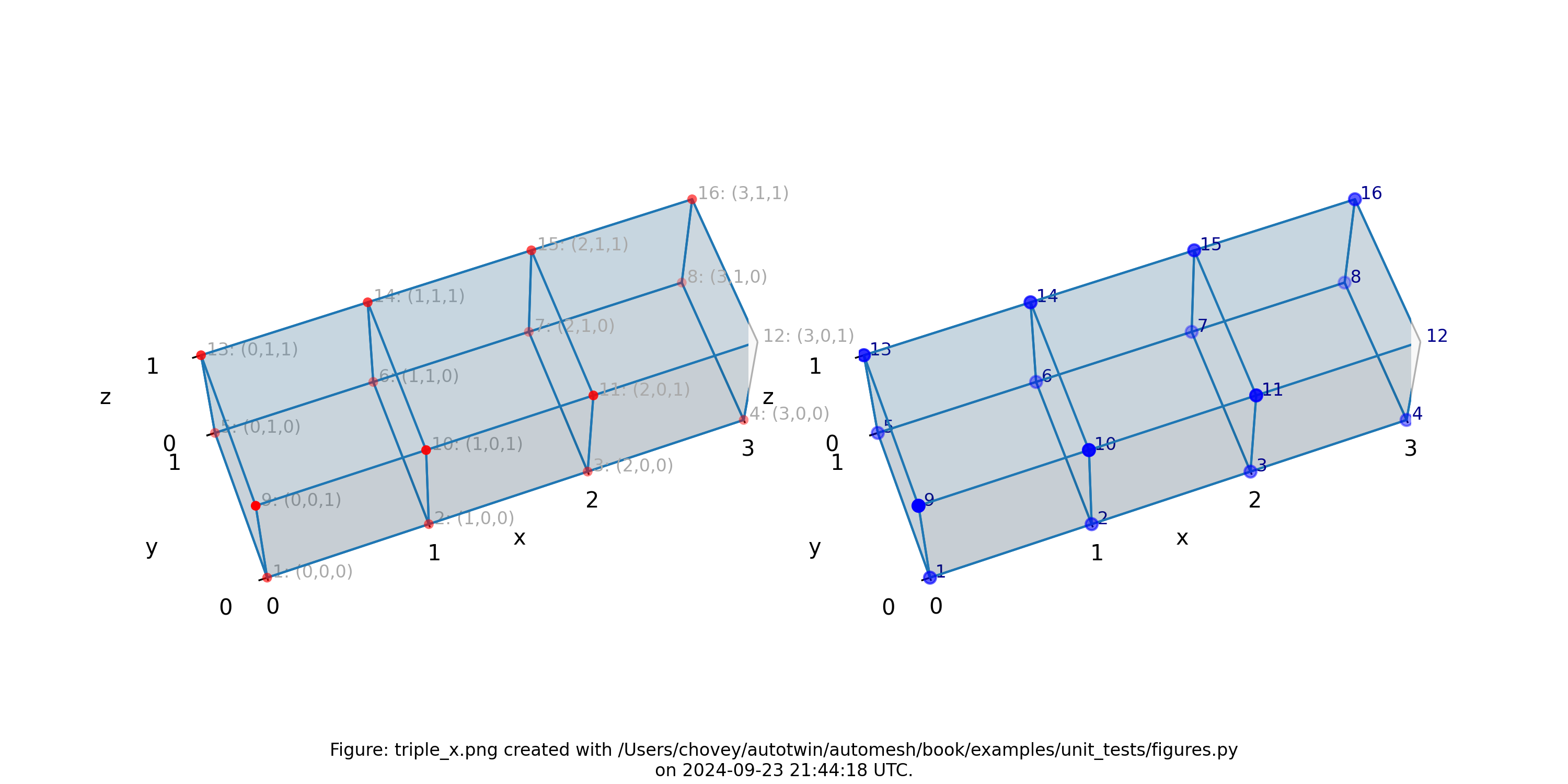
Figure: Mesh composed of a single block with three elements, propagating along
the x-axis, (left) lattice node numbers, (right) mesh node numbers.
Quadruple
11 # x:1 y:1 z:1
11 # 2 1 1
11 # 3 1 1
11 # 4 1 1
where the segmentation 11 denotes block 11 in the finite element mesh.
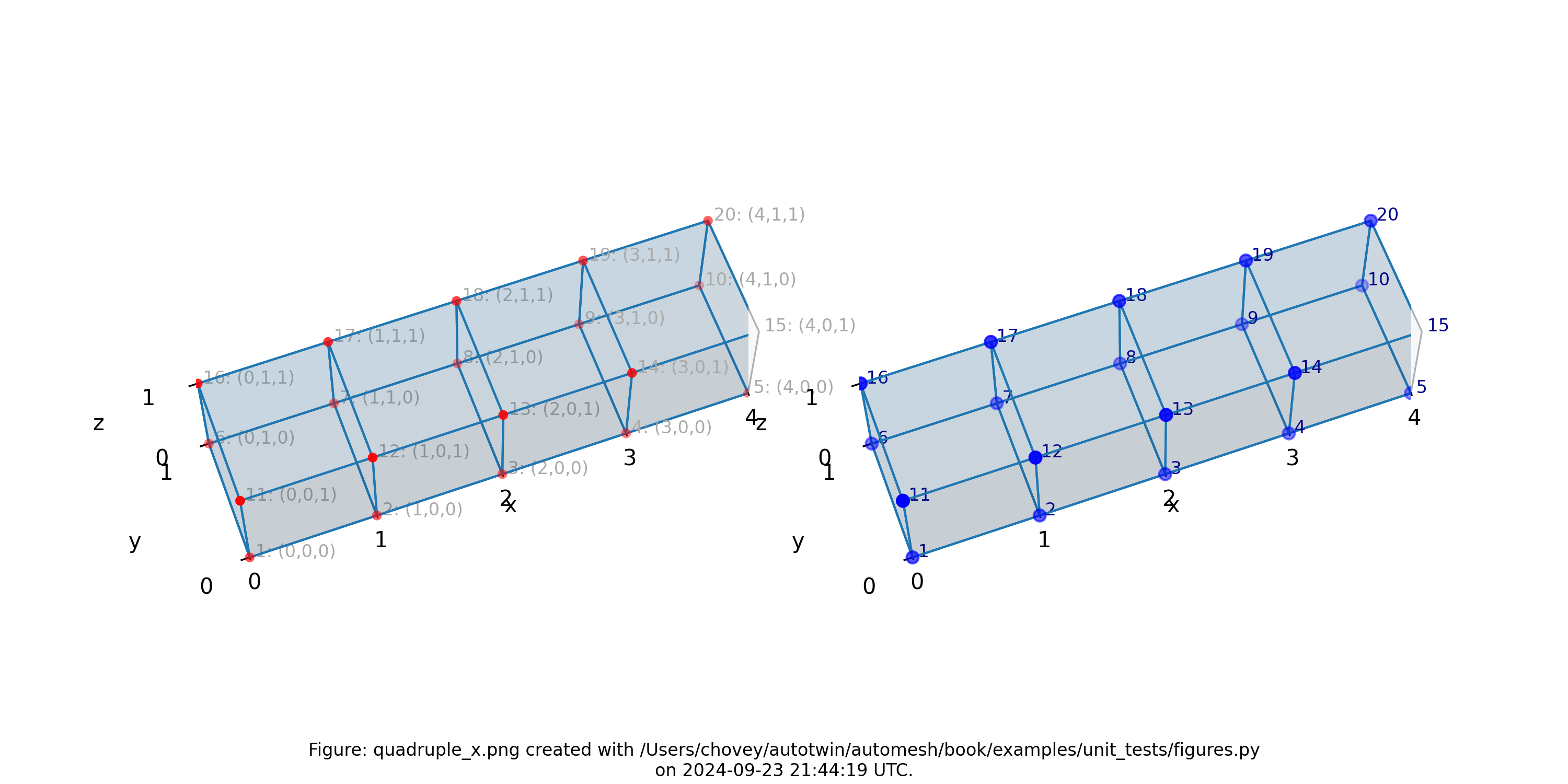
Figure: Mesh composed of a single block with four elements, propagating along
the x-axis, (left) lattice node numbers, (right) mesh node numbers.
Quadruple with Voids
99 # x:1 y:1 z:1
0 # 2 1 1
0 # 3 1 1
99 # 4 1 1
where the segmentation 99 denotes block 99 in the finite element mesh, and segmentation 0 is excluded from the mesh.
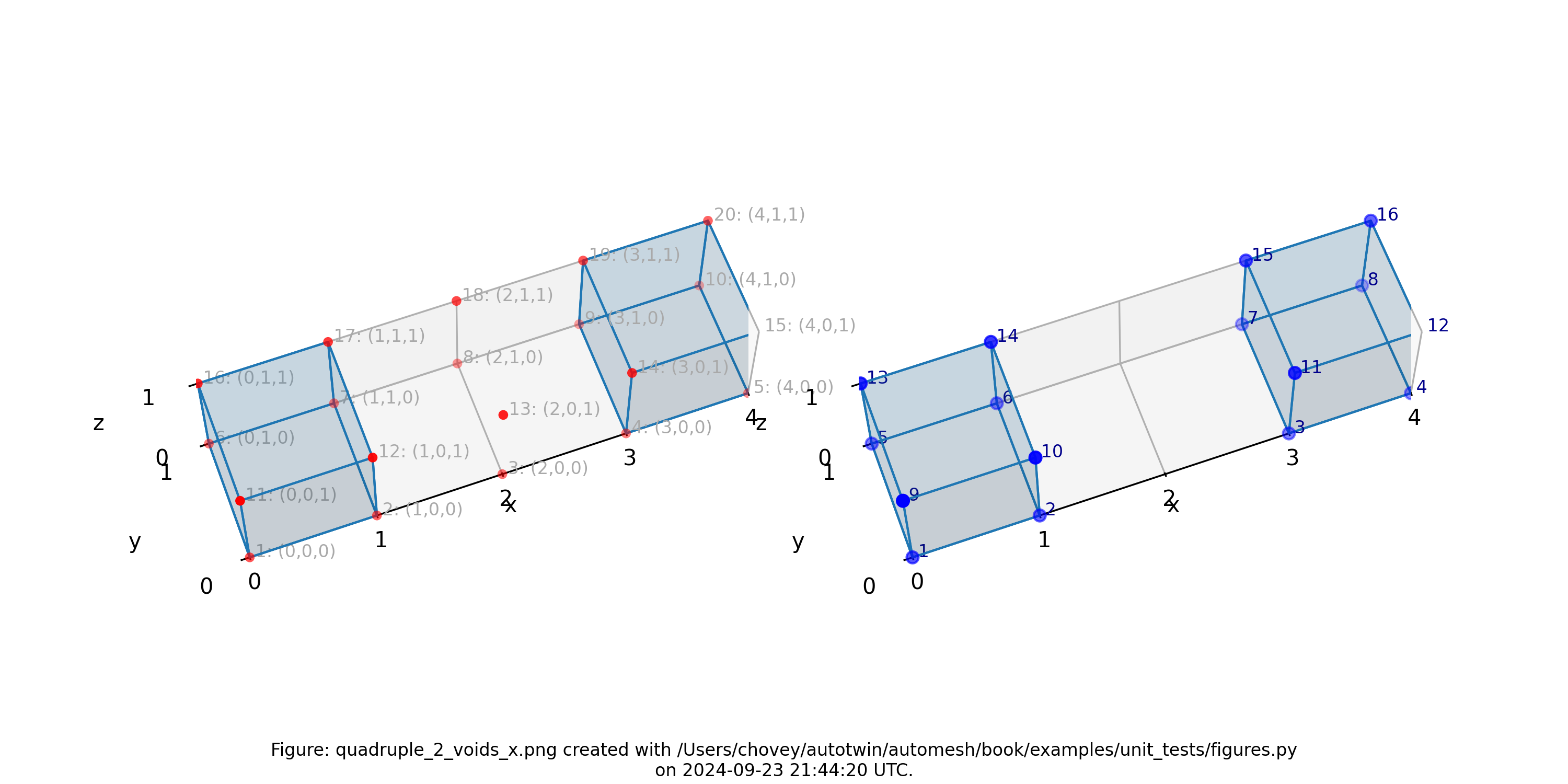
Figure: Mesh composed of a single block with two elements, propagating along
the x-axis and two voids, (left) lattice node numbers, (right) mesh node
numbers.
Quadruple with Two Blocks
100 # x:1 y:1 z:1
101 # 2 1 1
101 # 3 1 1
100 # 4 1 1
where the segmentation 100 and 101 denotes block 100 and 101,
respectively in the finite element mesh.
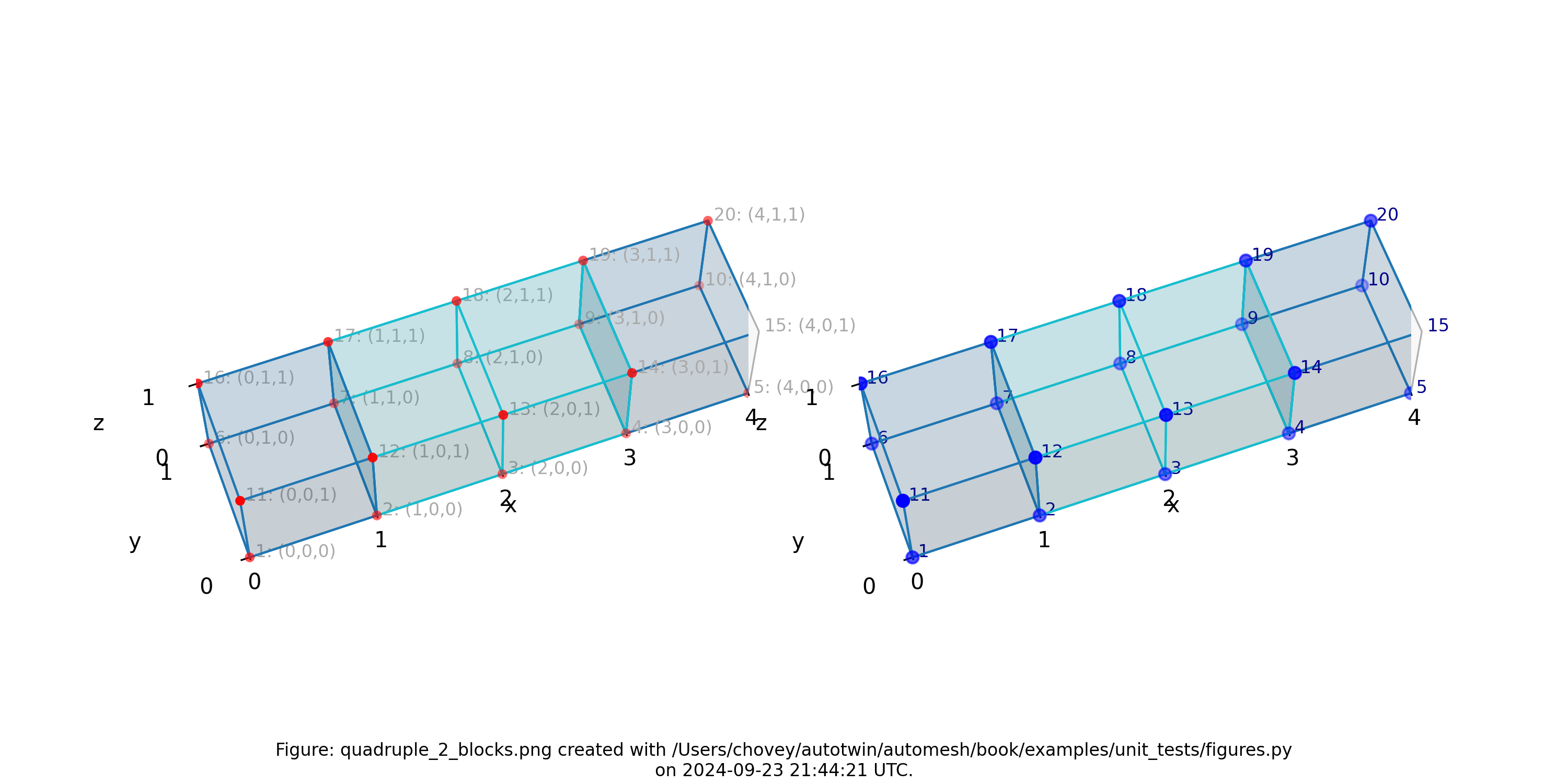
Figure: Mesh composed of two blocks with two elements elements each,
propagating along the x-axis, (left) lattice node numbers, (right) mesh
node numbers.
Quadruple with Two Blocks and Void
102 # x:1 y:1 z:1
103 # 2 1 1
0 # 3 1 1
102 # 4 1 1
where the segmentation 102 and 103 denotes block 102 and 103,
respectively, in the finite element mesh, and segmentation 0 will be included from the finite element mesh.
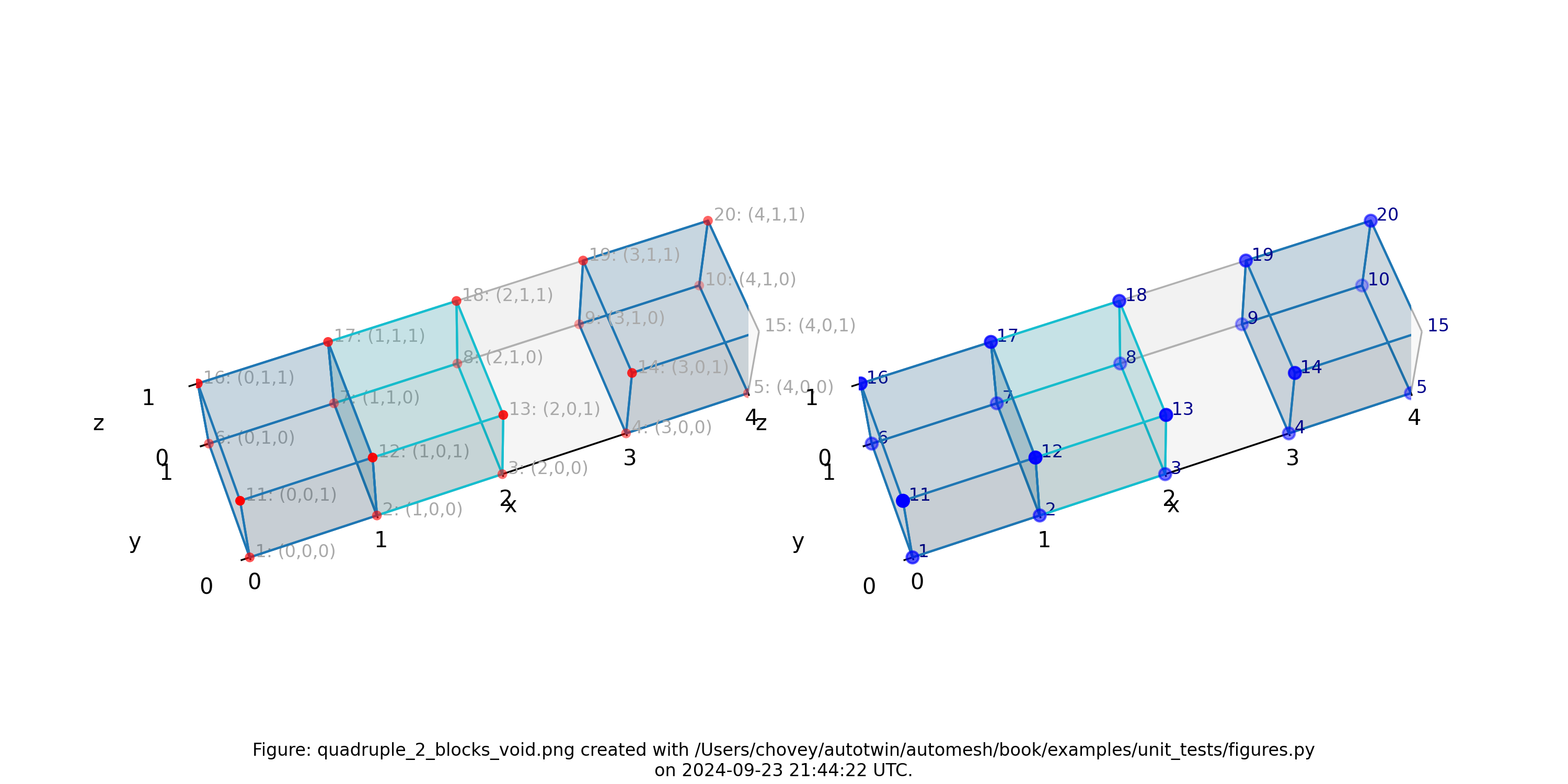
Figure: Mesh composed of one block with two elements, a second block with one
element, and a void, propagating along the x-axis, (left) lattice node
numbers, (right) mesh node numbers.
Cube
11 # x:1 y:1 z:1
11 # _ 2 _ 1 1
11 # 1 2 1
11 # _ 2 _ 2 _ 1
11 # 1 1 2
11 # _ 2 _ 1 2
11 # 1 2 2
11 # _ 2 _ 2 _ 2
where the segmentation 11 denotes block 11 in the finite element mesh.
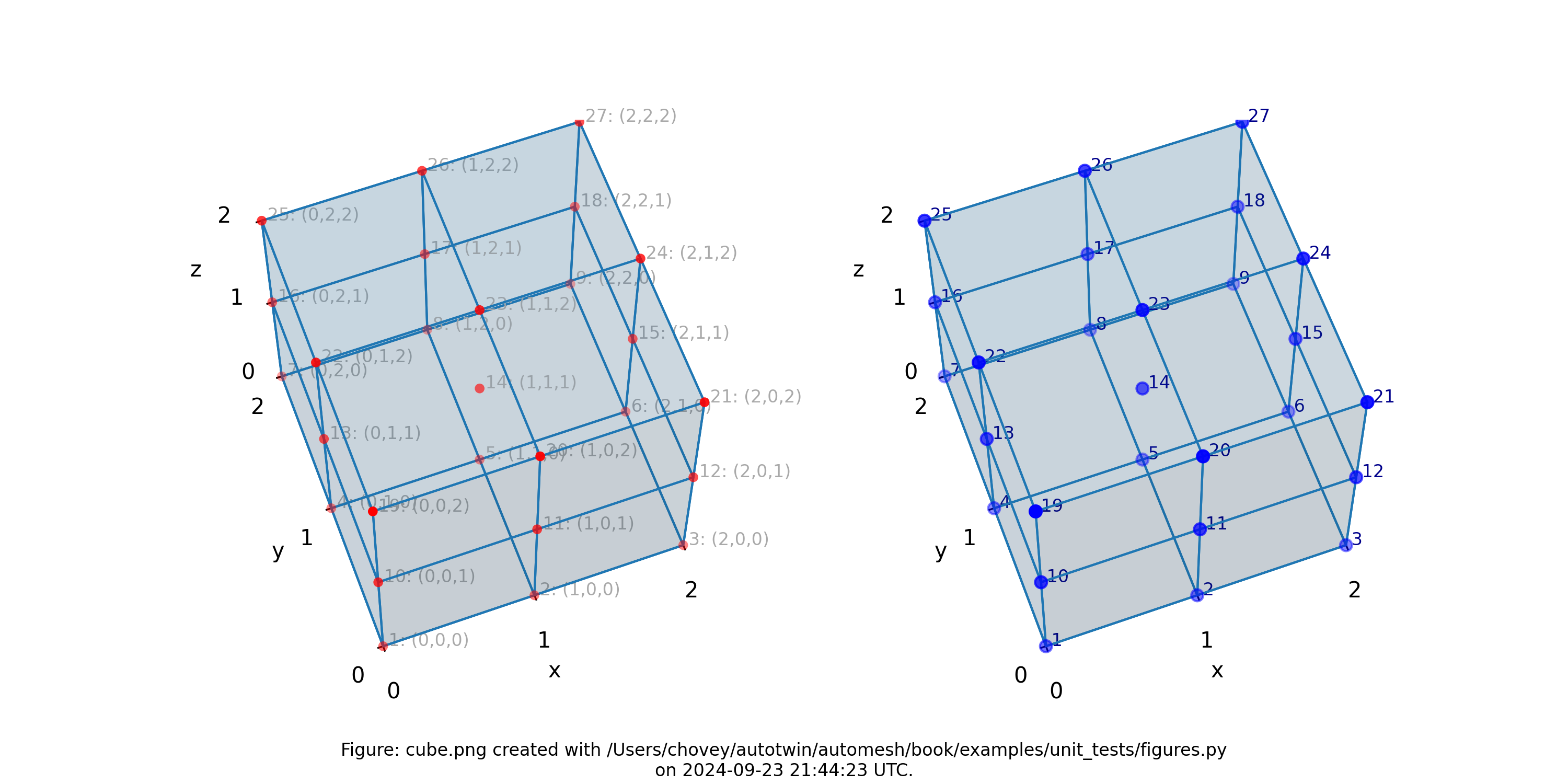
Figure: Mesh composed of one block with eight elements, (left) lattice node numbers, (right) mesh node numbers.
Cube with Multi Blocks and Void
82 # x:1 y:1 z:1
2 # _ 2 _ 1 1
2 # 1 2 1
2 # _ 2 _ 2 _ 1
0 # 1 1 2
31 # _ 2 _ 1 2
0 # 1 2 2
44 # _ 2 _ 2 _ 2
where the segmentation 82, 2, 31 and 44 denotes block 82, 2, 31
and 44, respectively, in the finite element mesh, and segmentation 0 will
be included from the finite element mesh.
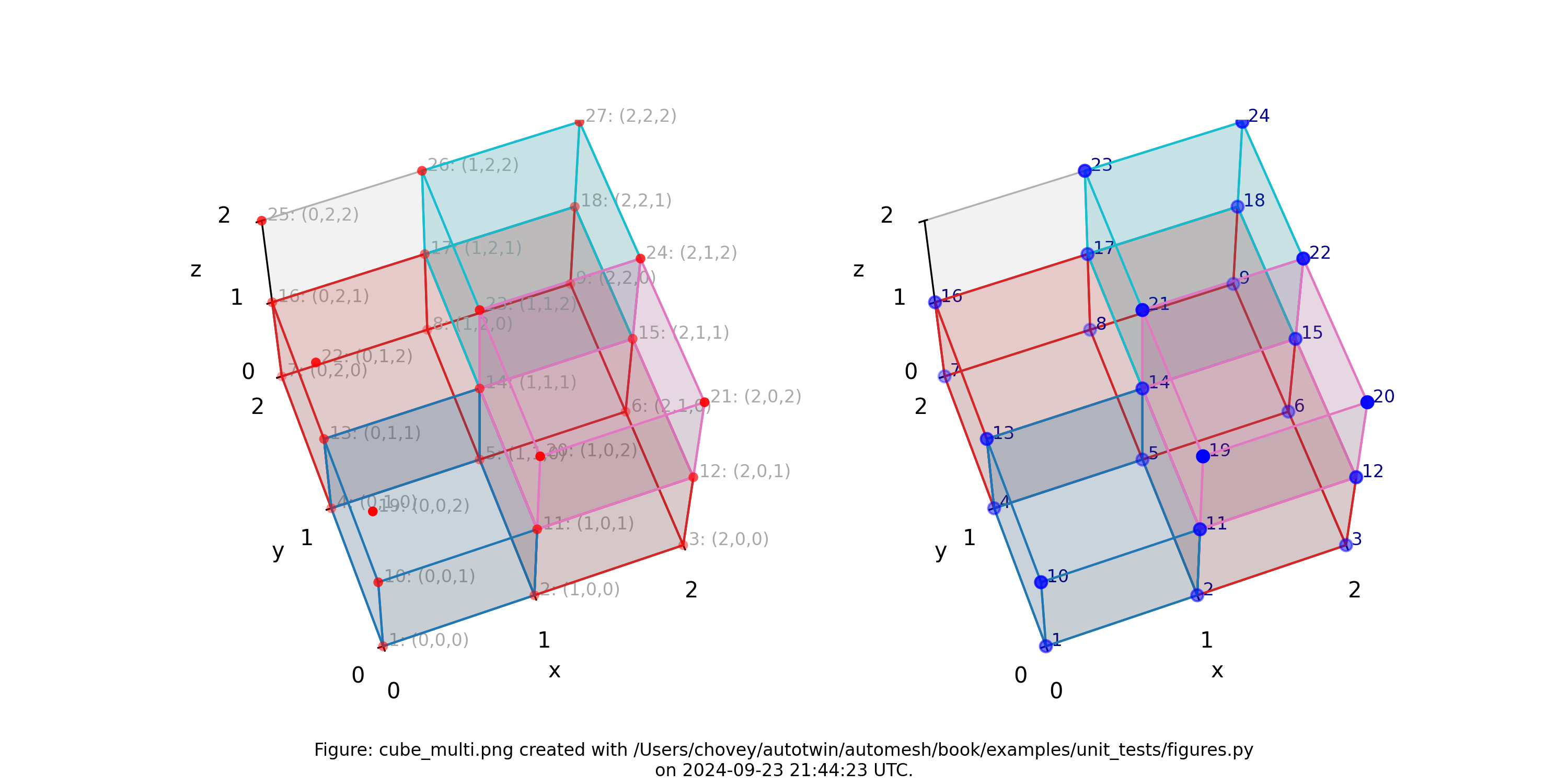
Figure: Mesh composed of four blocks (block 82 has one element, block 2
has three elements, block 31 has one element, and block 44 has one
element), (left) lattice node numbers, (right) mesh node numbers.
Cube with Inclusion
11 # x:1 y:1 z:1
11 # 2 1 1
11 # _ 3 _ 1 1
11 # 1 2 1
11 # 2 2 1
11 # _ 3 _ 2 1
11 # 1 3 1
11 # 2 3 1
11 # _ 3 _ 3 _ 1
11 # 1 1 2
11 # 2 1 2
11 # _ 3 _ 1 2
11 # 1 2 2
88 # 2 2 2
11 # _ 3 _ 2 2
11 # 1 3 2
11 # 2 3 2
11 # _ 3 _ 3 _ 2
11 # 1 1 3
11 # 2 1 3
11 # _ 3 _ 1 3
11 # 1 2 3
11 # 2 2 3
11 # _ 3 _ 2 3
11 # 1 3 3
11 # 2 3 3
11 # _ 3 _ 3 _ 3
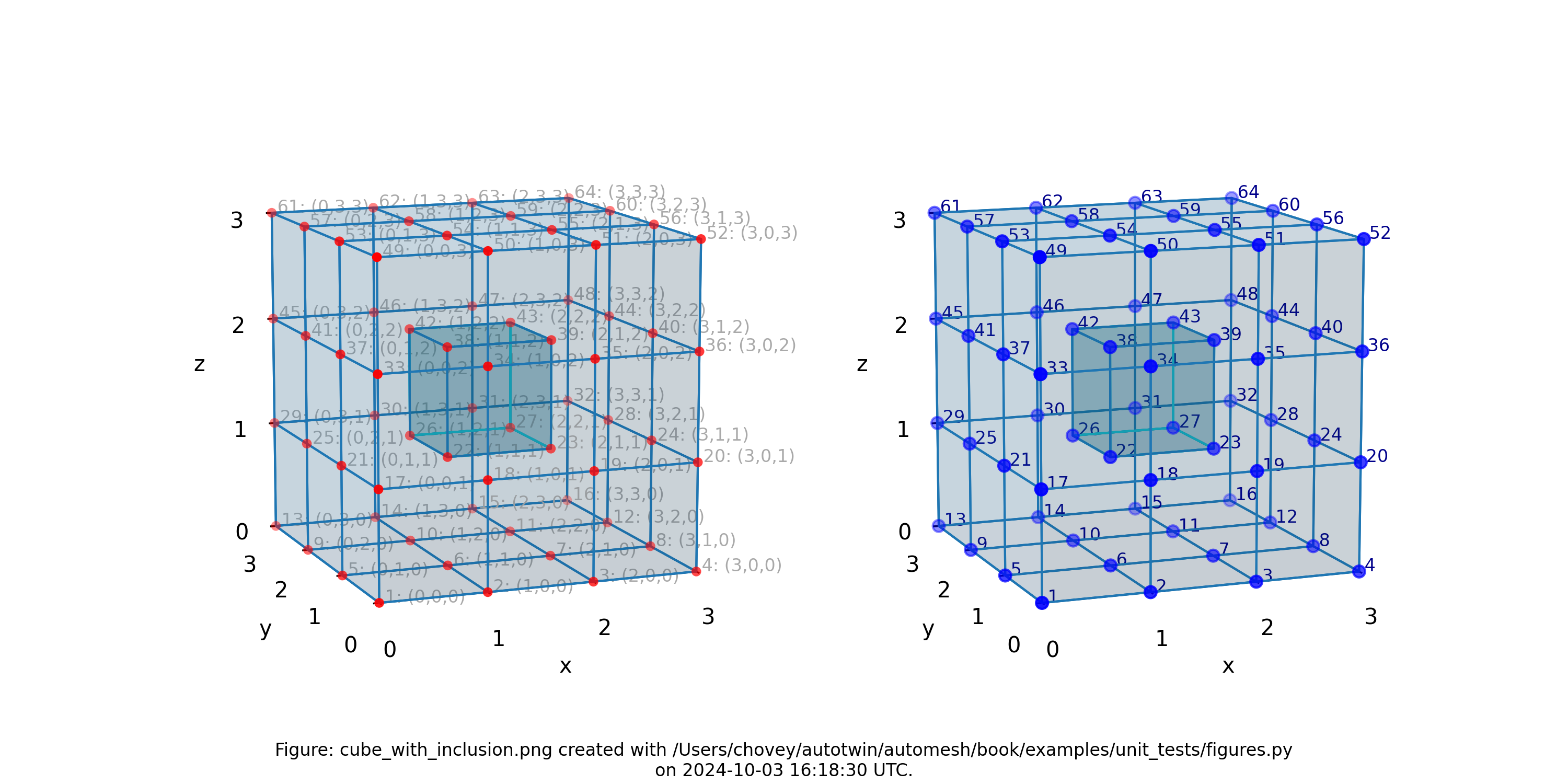
Figure: Mesh composed of 26 voxels of (block 11) and one voxel inslusion
(block 88), (left) lattice node numbers, (right) mesh node numbers.
Bracket
1 # x:1 y:1 z:1
1 # 2 1 1
1 # 3 1 1
1 # _ 4 _ 1 1
1 # x:1 y:2 z:1
1 # 2 2 1
1 # 3 2 1
1 # _ 4 _ 2 1
1 # x:1 y:3 z:1
1 # 2 3 1
0 # 3 3 1
0 # _ 4 _ 3 1
1 # x:1 y:4 z:1
1 # 2 4 1
0 # 3 4 1
0 # _ 4 _ 4 1
where the segmentation 1 denotes block 1 in the finite element mesh,
and segmentation 0 is excluded from the mesh.

Figure: Mesh composed of a L-shaped bracket in the xy plane.
Letter F
11 # x:1 y:1 z:1
0 # 2 1 1
0 # _ 3 _ 1 1
11 # 1 2 1
0 # 2 2 1
0 # _ 3 _ 2 1
11 # 1 3 1
11 # 2 3 1
0 # _ 3 _ 3 1
11 # 1 4 1
0 # 2 4 1
0 # _ 3 _ 4 1
11 # 1 5 1
11 # 2 5 1
11 # _ 3 _ 5 _ 1
where the segmentation 11 denotes block 11 in the finite element mesh.
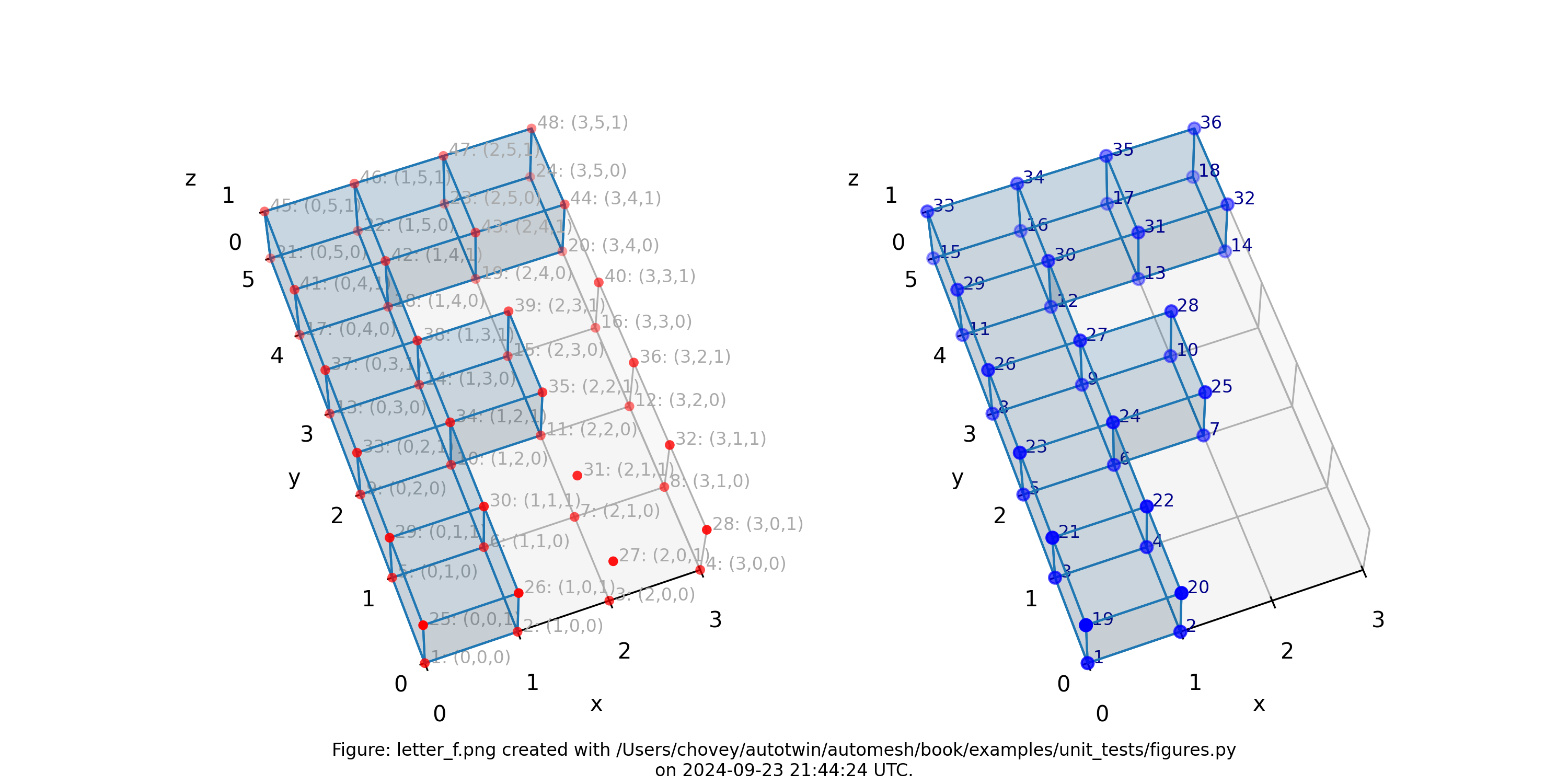
Figure: Mesh composed of a single block with eight elements, (left) lattice node numbers, (right) mesh node numbers.
Letter F in 3D
1 # x:1 y:1 z:1
1 # 2 1 1
1 # 3 1 1
1 # _ 4 _ 1 1
1 # 1 2 1
1 # 2 2 1
1 # 3 2 1
1 # _ 4 _ 2 1
1 # 1 3 1
1 # 2 3 1
1 # 3 3 1
1 # _ 4 _ 3 1
1 # 1 4 1
1 # 2 4 1
1 # 3 4 1
1 # _ 4 _ 4 1
1 # 1 5 1
1 # 2 5 1
1 # 3 5 1
1 # _ 4 _ 5 _ 1
1 # x:1 y:1 z:2
0 # 2 1 2
0 # 3 1 2
0 # _ 4 _ 1 2
1 # 1 2 2
0 # 2 2 2
0 # 3 2 2
0 # _ 4 _ 2 2
1 # 1 3 2
1 # 2 3 2
1 # 3 3 2
1 # _ 4 _ 3 2
1 # 1 4 2
0 # 2 4 2
0 # 3 4 2
0 # _ 4 _ 4 2
1 # 1 5 2
1 # 2 5 2
1 # 3 5 2
1 # _ 4 _ 5 _ 2
1 # x:1 y:1 z:3
0 # 2 1 j
0 # 3 1 2
0 # _ 4 _ 1 2
1 # 1 2 3
0 # 2 2 3
0 # 3 2 3
0 # _ 4 _ 2 3
1 # 1 3 3
0 # 2 3 3
0 # 3 3 3
0 # _ 4 _ 3 3
1 # 1 4 3
0 # 2 4 3
0 # 3 4 3
0 # _ 4 _ 4 3
1 # 1 5 3
1 # 2 5 3
1 # 3 5 3
1 # _ 4 _ 5 _ 3
which corresponds to --nelx 4, --nely 5, and --nelz 3 in the
command line interface.
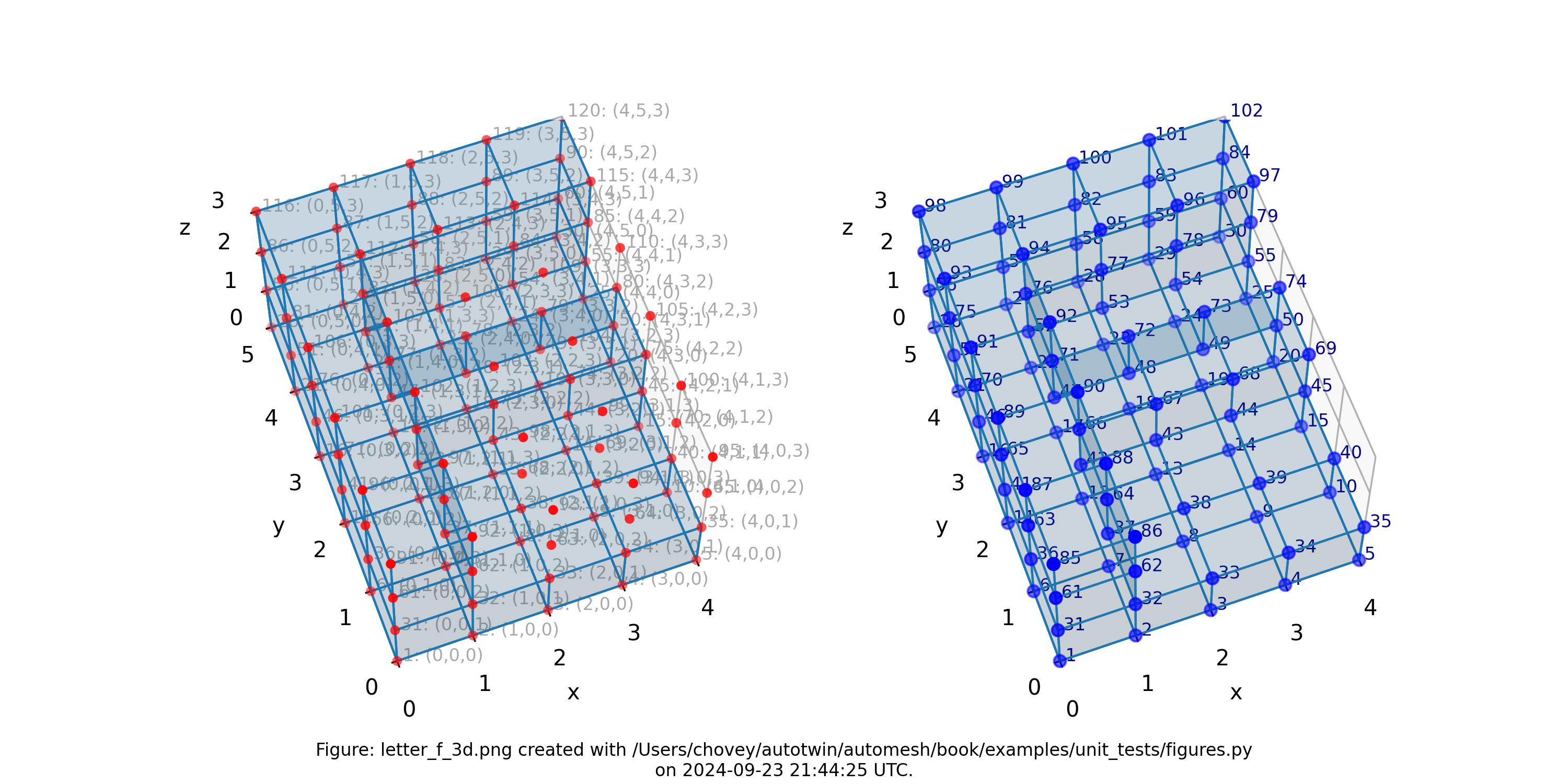
Figure: Mesh composed of a single block with thirty-nine elements, (left) lattice node numbers, (right) mesh node numbers.
The shape of the solid segmentation is more easily seen without the lattice and element nodes, and with decreased opacity, as shown below:

Figure: Mesh composed of a single block with thirty-nine elements, shown with decreased opacity and without lattice and element node numbers.
Sparse
0 # x:1 y:1 z:1
0 # 2 1 1
0 # 3 1 1
0 # 4 1 1
2 # _ 5 _ 1 1
0 # 1 2 1
1 # 2 2 1
0 # 3 2 1
0 # 4 2 1
2 # _ 5 _ 2 1
1 # 1 3 1
2 # 2 3 1
0 # 3 3 1
2 # 4 3 1
0 # _ 5 _ 3 1
0 # 1 4 1
1 # 2 4 1
0 # 3 4 1
2 # 4 4 1
0 # _ 5 _ 4 1
1 # 1 5 1
0 # 2 5 1
0 # 3 5 1
0 # 4 5 1
1 # _ 5 _ 5 _ 1
2 # x:1 y:1 z:2
0 # 2 1 2
2 # 3 1 2
0 # 4 1 2
0 # _ 5 _ 1 2
1 # 1 2 2
1 # 2 2 2
0 # 3 2 2
2 # 4 2 2
2 # _ 5 _ 2 2
2 # 1 3 2
0 # 2 3 2
0 # 3 3 2
0 # 4 3 2
0 # _ 5 _ 3 2
1 # 1 4 2
0 # 2 4 2
0 # 3 4 2
2 # 4 4 2
0 # _ 5 _ 4 2
2 # 1 5 2
0 # 2 5 2
2 # 3 5 2
0 # 4 5 2
2 # _ 5 _ 5 _ 2
0 # x:1 y:1 z:3
0 # 2 1 3
1 # 3 1 3
0 # 4 1 3
2 # _ 5 _ 1 3
0 # 1 2 3
0 # 2 2 3
0 # 3 2 3
1 # 4 2 3
2 # _ 5 _ 2 3
0 # 1 3 3
0 # 2 3 3
2 # 3 3 3
2 # 4 3 3
2 # _ 5 _ 3 3
0 # 1 4 3
0 # 2 4 3
1 # 3 4 3
0 # 4 4 3
1 # _ 5 _ 4 3
0 # 1 5 3
1 # 2 5 3
0 # 3 5 3
1 # 4 5 3
0 # _ 5 _ 5 _ 3
0 # x:1 y:1 z:4
1 # 2 1 4
2 # 3 1 4
1 # 4 1 4
2 # _ 5 _ 1 4
2 # 1 2 4
0 # 2 2 4
2 # 3 2 4
0 # 4 2 4
1 # _ 5 _ 2 4
1 # 1 3 4
2 # 2 3 4
2 # 3 3 4
0 # 4 3 4
0 # _ 5 _ 3 4
2 # 1 4 4
1 # 2 4 4
1 # 3 4 4
1 # 4 4 4
1 # _ 5 _ 4 4
0 # 1 5 4
0 # 2 5 4
1 # 3 5 4
0 # 4 5 4
0 # _ 5 _ 5 _ 4
0 # x:1 y:1 z:5
1 # 2 1 5
0 # 3 1 5
2 # 4 1 5
0 # _ 5 _ 1 5
1 # 1 2 5
0 # 2 2 5
0 # 3 2 5
0 # 4 2 5
2 # _ 5 _ 2 5
0 # 1 3 5
1 # 2 3 5
0 # 3 3 5
0 # 4 3 5
0 # _ 5 _ 3 5
1 # 1 4 5
0 # 2 4 5
0 # 3 4 5
0 # 4 4 5
0 # _ 5 _ 4 5
0 # 1 5 5
0 # 2 5 5
1 # 3 5 5
2 # 4 5 5
1 # _ 5 _ 5 _ 5
where the segmentation 1 denotes block 1 and segmentation 2 denotes block 2 in the finite eelement mesh (with segmentation 0 excluded).
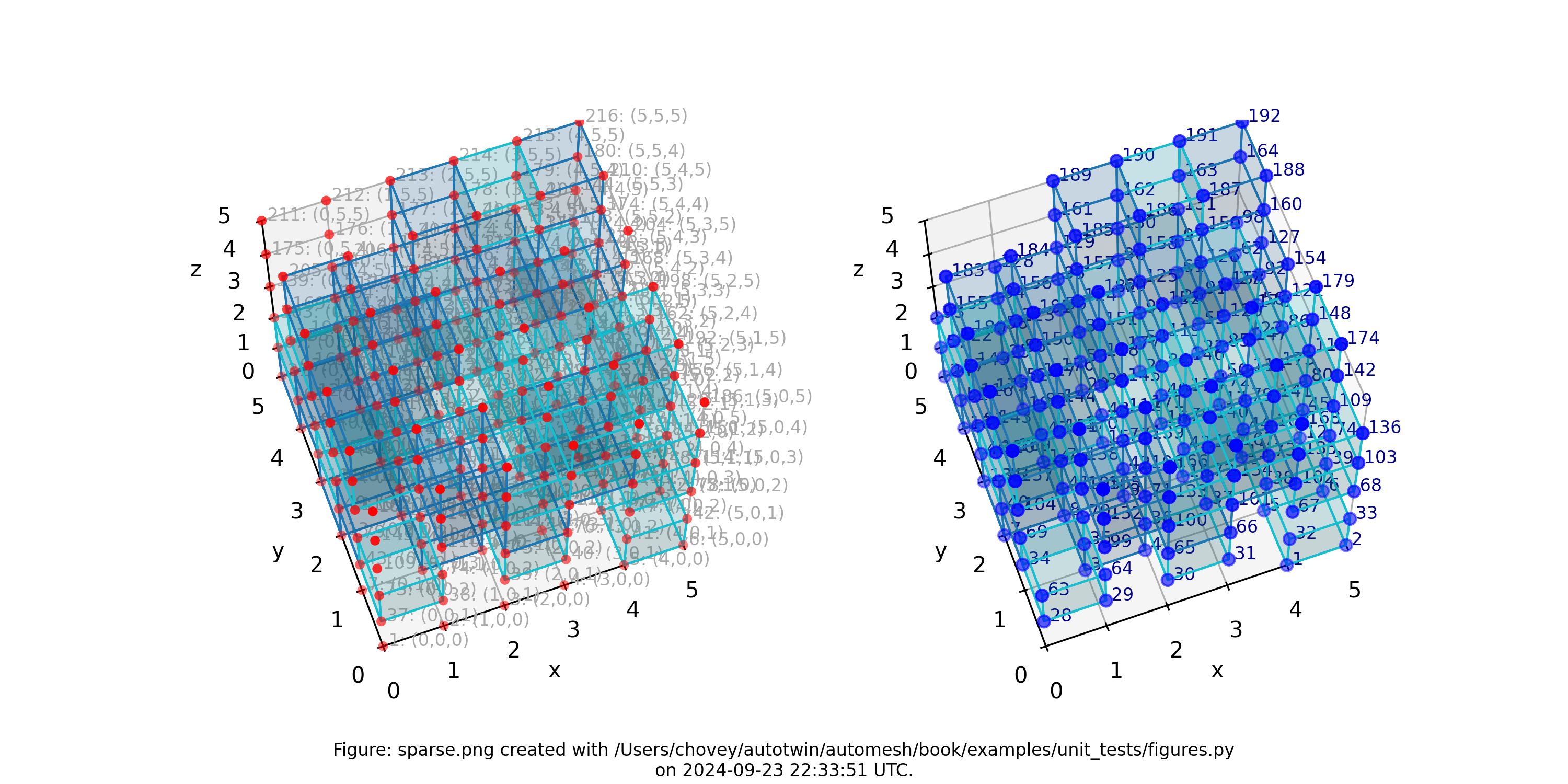
Figure: Sparse mesh composed of two materials at random voxel locations.
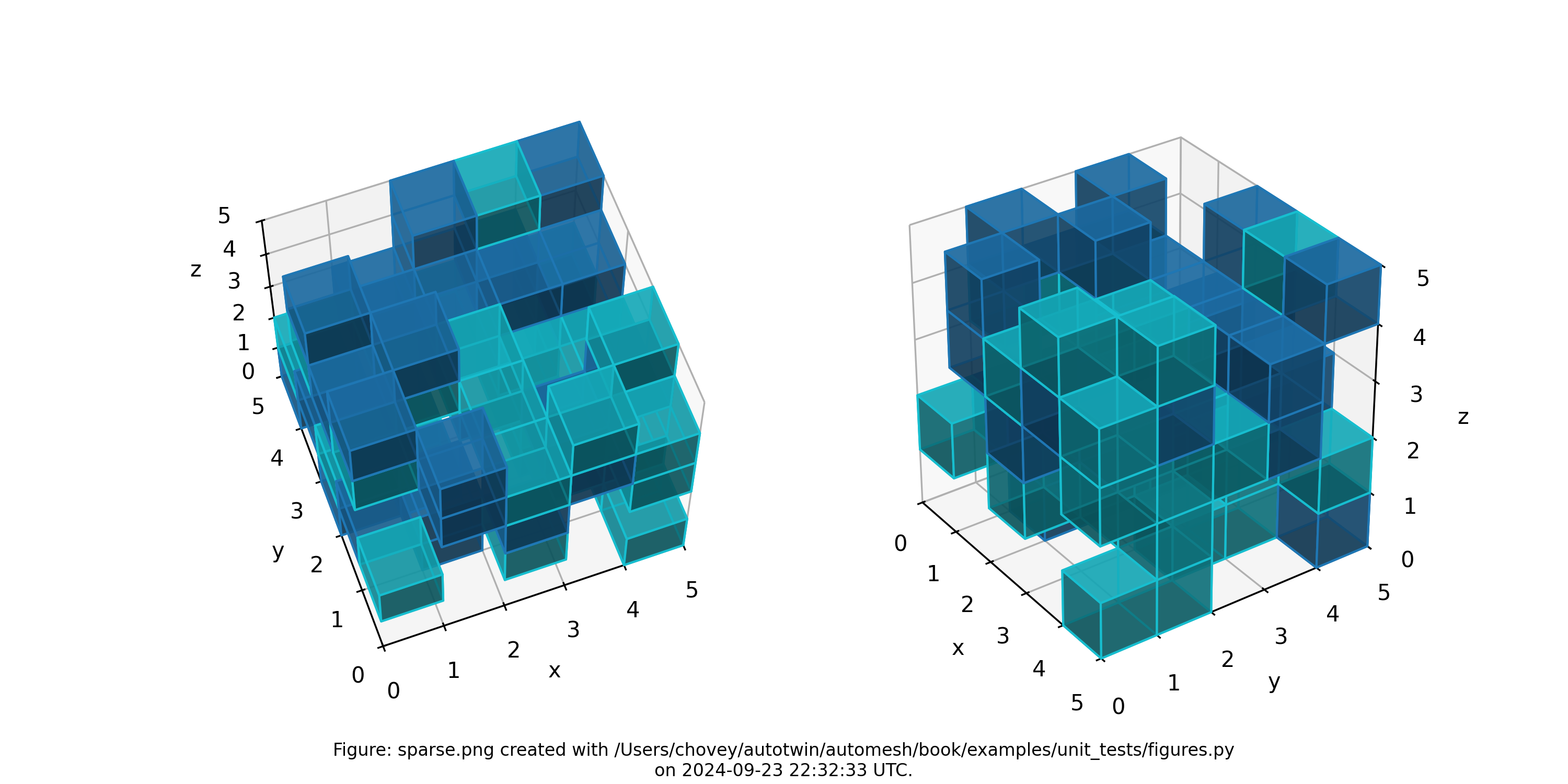
Figure: Sparse mesh composed of two materials at random voxel locations, shown with decreased opactity and without lattice and element node numbers.
Source
The figures were created with the following Python files:
examples_data.py
r"""This module, examples_data.py, contains the data for
the unit test examples.
"""
from typing import Final
import numpy as np
import examples_types as ty
# Type aliases
Example = ty.Example
COMMON_TITLE: Final[str] = "Lattice Index and Coordinates: "
class Single(Example):
"""A specific example of a single voxel."""
figure_title: str = COMMON_TITLE + "Single"
file_stem: str = "single"
segmentation = np.array(
[
[
[
11,
],
],
],
dtype=np.uint8,
)
included_ids = (11,)
gold_lattice = ((1, 2, 4, 3, 5, 6, 8, 7),)
gold_mesh_lattice_connectivity = (
(
11,
(1, 2, 4, 3, 5, 6, 8, 7),
),
)
gold_mesh_element_connectivity = (
(
11,
(1, 2, 4, 3, 5, 6, 8, 7),
),
)
class DoubleX(Example):
"""A specific example of a double voxel, coursed along the x-axis."""
figure_title: str = COMMON_TITLE + "DoubleX"
file_stem: str = "double_x"
segmentation = np.array(
[
[
[
11,
11,
],
],
],
dtype=np.uint8,
)
included_ids = (11,)
gold_lattice = (
(1, 2, 5, 4, 7, 8, 11, 10),
(2, 3, 6, 5, 8, 9, 12, 11),
)
gold_mesh_lattice_connectivity = (
(
11,
(1, 2, 5, 4, 7, 8, 11, 10),
(2, 3, 6, 5, 8, 9, 12, 11),
),
)
gold_mesh_element_connectivity = (
(
11,
(1, 2, 5, 4, 7, 8, 11, 10),
(2, 3, 6, 5, 8, 9, 12, 11),
),
)
class DoubleY(Example):
"""A specific example of a double voxel, coursed along the y-axis."""
figure_title: str = COMMON_TITLE + "DoubleY"
file_stem: str = "double_y"
segmentation = np.array(
[
[
[
11,
],
[
11,
],
],
],
dtype=np.uint8,
)
included_ids = (11,)
gold_lattice = (
(1, 2, 4, 3, 7, 8, 10, 9),
(3, 4, 6, 5, 9, 10, 12, 11),
)
gold_mesh_lattice_connectivity = (
(
11,
(1, 2, 4, 3, 7, 8, 10, 9),
(3, 4, 6, 5, 9, 10, 12, 11),
),
)
gold_mesh_element_connectivity = (
(
11,
(1, 2, 4, 3, 7, 8, 10, 9),
(3, 4, 6, 5, 9, 10, 12, 11),
),
)
class TripleX(Example):
"""A triple voxel lattice, coursed along the x-axis."""
figure_title: str = COMMON_TITLE + "Triple"
file_stem: str = "triple_x"
segmentation = np.array(
[
[
[
11,
11,
11,
],
],
],
dtype=np.uint8,
)
included_ids = (11,)
gold_lattice = (
(1, 2, 6, 5, 9, 10, 14, 13),
(2, 3, 7, 6, 10, 11, 15, 14),
(3, 4, 8, 7, 11, 12, 16, 15),
)
gold_mesh_lattice_connectivity = (
(
11,
(1, 2, 6, 5, 9, 10, 14, 13),
(2, 3, 7, 6, 10, 11, 15, 14),
(3, 4, 8, 7, 11, 12, 16, 15),
),
)
gold_mesh_element_connectivity = (
(
11,
(1, 2, 6, 5, 9, 10, 14, 13),
(2, 3, 7, 6, 10, 11, 15, 14),
(3, 4, 8, 7, 11, 12, 16, 15),
),
)
class QuadrupleX(Example):
"""A quadruple voxel lattice, coursed along the x-axis."""
figure_title: str = COMMON_TITLE + "Quadruple"
file_stem: str = "quadruple_x"
segmentation = np.array(
[
[
[
11,
11,
11,
11,
],
],
],
dtype=np.uint8,
)
included_ids = (11,)
gold_lattice = (
(1, 2, 7, 6, 11, 12, 17, 16),
(2, 3, 8, 7, 12, 13, 18, 17),
(3, 4, 9, 8, 13, 14, 19, 18),
(4, 5, 10, 9, 14, 15, 20, 19),
)
gold_mesh_lattice_connectivity = (
(
11,
(1, 2, 7, 6, 11, 12, 17, 16),
(2, 3, 8, 7, 12, 13, 18, 17),
(3, 4, 9, 8, 13, 14, 19, 18),
(4, 5, 10, 9, 14, 15, 20, 19),
),
)
gold_mesh_element_connectivity = (
(
11,
(1, 2, 7, 6, 11, 12, 17, 16),
(2, 3, 8, 7, 12, 13, 18, 17),
(3, 4, 9, 8, 13, 14, 19, 18),
(4, 5, 10, 9, 14, 15, 20, 19),
),
)
class Quadruple2VoidsX(Example):
"""A quadruple voxel lattice, coursed along the x-axis, with two
intermediate voxels in the segmentation being void.
"""
figure_title: str = COMMON_TITLE + "Quadruple2VoidsX"
file_stem: str = "quadruple_2_voids_x"
segmentation = np.array(
[
[
[
99,
0,
0,
99,
],
],
],
dtype=np.uint8,
)
included_ids = (99,)
gold_lattice = (
(1, 2, 7, 6, 11, 12, 17, 16),
(2, 3, 8, 7, 12, 13, 18, 17),
(3, 4, 9, 8, 13, 14, 19, 18),
(4, 5, 10, 9, 14, 15, 20, 19),
)
gold_mesh_lattice_connectivity = (
(
99,
(1, 2, 7, 6, 11, 12, 17, 16),
(4, 5, 10, 9, 14, 15, 20, 19),
),
)
gold_mesh_element_connectivity = (
(
99,
(1, 2, 6, 5, 9, 10, 14, 13),
(3, 4, 8, 7, 11, 12, 16, 15),
),
)
class Quadruple2Blocks(Example):
"""A quadruple voxel lattice, with the first intermediate voxel being
the second block and the second intermediate voxel being void.
"""
figure_title: str = COMMON_TITLE + "Quadruple2Blocks"
file_stem: str = "quadruple_2_blocks"
segmentation = np.array(
[
[
[
100,
101,
101,
100,
],
],
],
dtype=np.uint8,
)
included_ids = (
100,
101,
)
gold_lattice = (
(1, 2, 7, 6, 11, 12, 17, 16),
(2, 3, 8, 7, 12, 13, 18, 17),
(3, 4, 9, 8, 13, 14, 19, 18),
(4, 5, 10, 9, 14, 15, 20, 19),
)
gold_mesh_lattice_connectivity = (
(
100,
(1, 2, 7, 6, 11, 12, 17, 16),
(4, 5, 10, 9, 14, 15, 20, 19),
),
(
101,
(2, 3, 8, 7, 12, 13, 18, 17),
(3, 4, 9, 8, 13, 14, 19, 18),
),
)
gold_mesh_element_connectivity = (
(
100,
(1, 2, 7, 6, 11, 12, 17, 16),
(4, 5, 10, 9, 14, 15, 20, 19),
),
(
101,
(2, 3, 8, 7, 12, 13, 18, 17),
(3, 4, 9, 8, 13, 14, 19, 18),
),
)
class Quadruple2BlocksVoid(Example):
"""A quadruple voxel lattice, with the first intermediate voxel being
the second block and the second intermediate voxel being void.
"""
figure_title: str = COMMON_TITLE + "Quadruple2BlocksVoid"
file_stem: str = "quadruple_2_blocks_void"
segmentation = np.array(
[
[
[
102,
103,
0,
102,
],
],
],
dtype=np.uint8,
)
included_ids = (
102,
103,
)
gold_lattice = (
(1, 2, 7, 6, 11, 12, 17, 16),
(2, 3, 8, 7, 12, 13, 18, 17),
(3, 4, 9, 8, 13, 14, 19, 18),
(4, 5, 10, 9, 14, 15, 20, 19),
)
gold_mesh_lattice_connectivity = (
(
102,
(1, 2, 7, 6, 11, 12, 17, 16),
(4, 5, 10, 9, 14, 15, 20, 19),
),
(
103,
(2, 3, 8, 7, 12, 13, 18, 17),
),
)
gold_mesh_element_connectivity = (
(
102,
(1, 2, 7, 6, 11, 12, 17, 16),
(4, 5, 10, 9, 14, 15, 20, 19),
),
(
103,
(2, 3, 8, 7, 12, 13, 18, 17),
),
)
class Cube(Example):
"""A (2 x 2 x 2) voxel cube."""
figure_title: str = COMMON_TITLE + "Cube"
file_stem: str = "cube"
segmentation = np.array(
[
[
[
11,
11,
],
[
11,
11,
],
],
[
[
11,
11,
],
[
11,
11,
],
],
],
dtype=np.uint8,
)
included_ids = (11,)
gold_lattice = (
(1, 2, 5, 4, 10, 11, 14, 13),
(2, 3, 6, 5, 11, 12, 15, 14),
(4, 5, 8, 7, 13, 14, 17, 16),
(5, 6, 9, 8, 14, 15, 18, 17),
(10, 11, 14, 13, 19, 20, 23, 22),
(11, 12, 15, 14, 20, 21, 24, 23),
(13, 14, 17, 16, 22, 23, 26, 25),
(14, 15, 18, 17, 23, 24, 27, 26),
)
gold_mesh_lattice_connectivity = (
(
11,
(1, 2, 5, 4, 10, 11, 14, 13),
(2, 3, 6, 5, 11, 12, 15, 14),
(4, 5, 8, 7, 13, 14, 17, 16),
(5, 6, 9, 8, 14, 15, 18, 17),
(10, 11, 14, 13, 19, 20, 23, 22),
(11, 12, 15, 14, 20, 21, 24, 23),
(13, 14, 17, 16, 22, 23, 26, 25),
(14, 15, 18, 17, 23, 24, 27, 26),
),
)
gold_mesh_element_connectivity = (
(
11,
(1, 2, 5, 4, 10, 11, 14, 13),
(2, 3, 6, 5, 11, 12, 15, 14),
(4, 5, 8, 7, 13, 14, 17, 16),
(5, 6, 9, 8, 14, 15, 18, 17),
(10, 11, 14, 13, 19, 20, 23, 22),
(11, 12, 15, 14, 20, 21, 24, 23),
(13, 14, 17, 16, 22, 23, 26, 25),
(14, 15, 18, 17, 23, 24, 27, 26),
),
)
class CubeMulti(Example):
"""A (2 x 2 x 2) voxel cube with two voids and six elements."""
figure_title: str = COMMON_TITLE + "CubeMulti"
file_stem: str = "cube_multi"
segmentation = np.array(
[
[
[
82,
2,
],
[
2,
2,
],
],
[
[
0,
31,
],
[
0,
44,
],
],
],
dtype=np.uint8,
)
included_ids = (
82,
2,
31,
44,
)
gold_lattice = (
(1, 2, 5, 4, 10, 11, 14, 13),
(2, 3, 6, 5, 11, 12, 15, 14),
(4, 5, 8, 7, 13, 14, 17, 16),
(5, 6, 9, 8, 14, 15, 18, 17),
(10, 11, 14, 13, 19, 20, 23, 22),
(11, 12, 15, 14, 20, 21, 24, 23),
(13, 14, 17, 16, 22, 23, 26, 25),
(14, 15, 18, 17, 23, 24, 27, 26),
)
gold_mesh_lattice_connectivity = (
# (
# 0,
# (10, 11, 14, 13, 19, 20, 23, 22),
# ),
# (
# 0,
# (13, 14, 17, 16, 22, 23, 26, 25),
(
2,
(2, 3, 6, 5, 11, 12, 15, 14),
(4, 5, 8, 7, 13, 14, 17, 16),
(5, 6, 9, 8, 14, 15, 18, 17),
),
(
31,
(11, 12, 15, 14, 20, 21, 24, 23),
),
(
44,
(14, 15, 18, 17, 23, 24, 27, 26),
),
(
82,
(1, 2, 5, 4, 10, 11, 14, 13),
),
)
gold_mesh_element_connectivity = (
(
2,
(2, 3, 6, 5, 11, 12, 15, 14),
(4, 5, 8, 7, 13, 14, 17, 16),
(5, 6, 9, 8, 14, 15, 18, 17),
),
(
31,
(11, 12, 15, 14, 19, 20, 22, 21),
),
(
44,
(14, 15, 18, 17, 21, 22, 24, 23),
),
(
82,
(1, 2, 5, 4, 10, 11, 14, 13),
),
)
class CubeWithInclusion(Example):
"""A (3 x 3 x 3) voxel cube with a single voxel inclusion
at the center.
"""
figure_title: str = COMMON_TITLE + "CubeWithInclusion"
file_stem: str = "cube_with_inclusion"
segmentation = np.array(
[
[
[
11,
11,
11,
],
[
11,
11,
11,
],
[
11,
11,
11,
],
],
[
[
11,
11,
11,
],
[
11,
88,
11,
],
[
11,
11,
11,
],
],
[
[
11,
11,
11,
],
[
11,
11,
11,
],
[
11,
11,
11,
],
],
],
dtype=np.uint8,
)
included_ids = (
11,
88,
)
gold_lattice = (
(1, 2, 6, 5, 17, 18, 22, 21),
(2, 3, 7, 6, 18, 19, 23, 22),
(3, 4, 8, 7, 19, 20, 24, 23),
(5, 6, 10, 9, 21, 22, 26, 25),
(6, 7, 11, 10, 22, 23, 27, 26),
(7, 8, 12, 11, 23, 24, 28, 27),
(9, 10, 14, 13, 25, 26, 30, 29),
(10, 11, 15, 14, 26, 27, 31, 30),
(11, 12, 16, 15, 27, 28, 32, 31),
(17, 18, 22, 21, 33, 34, 38, 37),
(18, 19, 23, 22, 34, 35, 39, 38),
(19, 20, 24, 23, 35, 36, 40, 39),
(21, 22, 26, 25, 37, 38, 42, 41),
(22, 23, 27, 26, 38, 39, 43, 42),
(23, 24, 28, 27, 39, 40, 44, 43),
(25, 26, 30, 29, 41, 42, 46, 45),
(26, 27, 31, 30, 42, 43, 47, 46),
(27, 28, 32, 31, 43, 44, 48, 47),
(33, 34, 38, 37, 49, 50, 54, 53),
(34, 35, 39, 38, 50, 51, 55, 54),
(35, 36, 40, 39, 51, 52, 56, 55),
(37, 38, 42, 41, 53, 54, 58, 57),
(38, 39, 43, 42, 54, 55, 59, 58),
(39, 40, 44, 43, 55, 56, 60, 59),
(41, 42, 46, 45, 57, 58, 62, 61),
(42, 43, 47, 46, 58, 59, 63, 62),
(43, 44, 48, 47, 59, 60, 64, 63),
)
gold_mesh_lattice_connectivity = (
(
11,
(1, 2, 6, 5, 17, 18, 22, 21),
(2, 3, 7, 6, 18, 19, 23, 22),
(3, 4, 8, 7, 19, 20, 24, 23),
(5, 6, 10, 9, 21, 22, 26, 25),
(6, 7, 11, 10, 22, 23, 27, 26),
(7, 8, 12, 11, 23, 24, 28, 27),
(9, 10, 14, 13, 25, 26, 30, 29),
(10, 11, 15, 14, 26, 27, 31, 30),
(11, 12, 16, 15, 27, 28, 32, 31),
(17, 18, 22, 21, 33, 34, 38, 37),
(18, 19, 23, 22, 34, 35, 39, 38),
(19, 20, 24, 23, 35, 36, 40, 39),
(21, 22, 26, 25, 37, 38, 42, 41),
(23, 24, 28, 27, 39, 40, 44, 43),
(25, 26, 30, 29, 41, 42, 46, 45),
(26, 27, 31, 30, 42, 43, 47, 46),
(27, 28, 32, 31, 43, 44, 48, 47),
(33, 34, 38, 37, 49, 50, 54, 53),
(34, 35, 39, 38, 50, 51, 55, 54),
(35, 36, 40, 39, 51, 52, 56, 55),
(37, 38, 42, 41, 53, 54, 58, 57),
(38, 39, 43, 42, 54, 55, 59, 58),
(39, 40, 44, 43, 55, 56, 60, 59),
(41, 42, 46, 45, 57, 58, 62, 61),
(42, 43, 47, 46, 58, 59, 63, 62),
(43, 44, 48, 47, 59, 60, 64, 63),
),
(
88,
(22, 23, 27, 26, 38, 39, 43, 42),
),
)
gold_mesh_element_connectivity = (
(
11,
(1, 2, 6, 5, 17, 18, 22, 21),
(2, 3, 7, 6, 18, 19, 23, 22),
(3, 4, 8, 7, 19, 20, 24, 23),
(5, 6, 10, 9, 21, 22, 26, 25),
(6, 7, 11, 10, 22, 23, 27, 26),
(7, 8, 12, 11, 23, 24, 28, 27),
(9, 10, 14, 13, 25, 26, 30, 29),
(10, 11, 15, 14, 26, 27, 31, 30),
(11, 12, 16, 15, 27, 28, 32, 31),
(17, 18, 22, 21, 33, 34, 38, 37),
(18, 19, 23, 22, 34, 35, 39, 38),
(19, 20, 24, 23, 35, 36, 40, 39),
(21, 22, 26, 25, 37, 38, 42, 41),
(23, 24, 28, 27, 39, 40, 44, 43),
(25, 26, 30, 29, 41, 42, 46, 45),
(26, 27, 31, 30, 42, 43, 47, 46),
(27, 28, 32, 31, 43, 44, 48, 47),
(33, 34, 38, 37, 49, 50, 54, 53),
(34, 35, 39, 38, 50, 51, 55, 54),
(35, 36, 40, 39, 51, 52, 56, 55),
(37, 38, 42, 41, 53, 54, 58, 57),
(38, 39, 43, 42, 54, 55, 59, 58),
(39, 40, 44, 43, 55, 56, 60, 59),
(41, 42, 46, 45, 57, 58, 62, 61),
(42, 43, 47, 46, 58, 59, 63, 62),
(43, 44, 48, 47, 59, 60, 64, 63),
),
(
88,
(22, 23, 27, 26, 38, 39, 43, 42),
),
)
class Bracket(Example):
"""An L-shape bracket in the xy plane."""
figure_title: str = COMMON_TITLE + "Bracket"
file_stem: str = "bracket"
segmentation = np.array(
[
[
[1, 1, 1, 1],
[1, 1, 1, 1],
[1, 1, 0, 0],
[1, 1, 0, 0],
],
]
)
included_ids = (1,)
gold_lattice = (
(1, 2, 7, 6, 26, 27, 32, 31),
(2, 3, 8, 7, 27, 28, 33, 32),
(3, 4, 9, 8, 28, 29, 34, 33),
(4, 5, 10, 9, 29, 30, 35, 34),
(6, 7, 12, 11, 31, 32, 37, 36),
(7, 8, 13, 12, 32, 33, 38, 37),
(8, 9, 14, 13, 33, 34, 39, 38),
(9, 10, 15, 14, 34, 35, 40, 39),
(11, 12, 17, 16, 36, 37, 42, 41),
(12, 13, 18, 17, 37, 38, 43, 42),
(13, 14, 19, 18, 38, 39, 44, 43),
(14, 15, 20, 19, 39, 40, 45, 44),
(16, 17, 22, 21, 41, 42, 47, 46),
(17, 18, 23, 22, 42, 43, 48, 47),
(18, 19, 24, 23, 43, 44, 49, 48),
(19, 20, 25, 24, 44, 45, 50, 49),
)
gold_mesh_lattice_connectivity = (
(
1,
(1, 2, 7, 6, 26, 27, 32, 31),
(2, 3, 8, 7, 27, 28, 33, 32),
(3, 4, 9, 8, 28, 29, 34, 33),
(4, 5, 10, 9, 29, 30, 35, 34),
(6, 7, 12, 11, 31, 32, 37, 36),
(7, 8, 13, 12, 32, 33, 38, 37),
(8, 9, 14, 13, 33, 34, 39, 38),
(9, 10, 15, 14, 34, 35, 40, 39),
(11, 12, 17, 16, 36, 37, 42, 41),
(12, 13, 18, 17, 37, 38, 43, 42),
(16, 17, 22, 21, 41, 42, 47, 46),
(17, 18, 23, 22, 42, 43, 48, 47),
),
)
gold_mesh_element_connectivity = (
(
1,
(1, 2, 7, 6, 22, 23, 28, 27),
(2, 3, 8, 7, 23, 24, 29, 28),
(3, 4, 9, 8, 24, 25, 30, 29),
(4, 5, 10, 9, 25, 26, 31, 30),
(6, 7, 12, 11, 27, 28, 33, 32),
(7, 8, 13, 12, 28, 29, 34, 33),
(8, 9, 14, 13, 29, 30, 35, 34),
(9, 10, 15, 14, 30, 31, 36, 35),
(11, 12, 17, 16, 32, 33, 38, 37),
(12, 13, 18, 17, 33, 34, 39, 38),
(16, 17, 20, 19, 37, 38, 41, 40),
(17, 18, 21, 20, 38, 39, 42, 41),
),
)
class LetterF(Example):
"""A minimal letter F example."""
figure_title: str = COMMON_TITLE + "LetterF"
file_stem: str = "letter_f"
segmentation = np.array(
[
[
[
11,
0,
0,
],
[
11,
0,
0,
],
[
11,
11,
0,
],
[
11,
0,
0,
],
[
11,
11,
11,
],
],
],
dtype=np.uint8,
)
included_ids = (11,)
gold_lattice = (
(1, 2, 6, 5, 25, 26, 30, 29),
(2, 3, 7, 6, 26, 27, 31, 30),
(3, 4, 8, 7, 27, 28, 32, 31),
(5, 6, 10, 9, 29, 30, 34, 33),
(6, 7, 11, 10, 30, 31, 35, 34),
(7, 8, 12, 11, 31, 32, 36, 35),
(9, 10, 14, 13, 33, 34, 38, 37),
(10, 11, 15, 14, 34, 35, 39, 38),
(11, 12, 16, 15, 35, 36, 40, 39),
(13, 14, 18, 17, 37, 38, 42, 41),
(14, 15, 19, 18, 38, 39, 43, 42),
(15, 16, 20, 19, 39, 40, 44, 43),
(17, 18, 22, 21, 41, 42, 46, 45),
(18, 19, 23, 22, 42, 43, 47, 46),
(19, 20, 24, 23, 43, 44, 48, 47),
)
gold_mesh_lattice_connectivity = (
(
11,
(1, 2, 6, 5, 25, 26, 30, 29),
# (2, 3, 7, 6, 26, 27, 31, 30),
# (3, 4, 8, 7, 27, 28, 32, 31),
(5, 6, 10, 9, 29, 30, 34, 33),
# (6, 7, 11, 10, 30, 31, 35, 34),
# (7, 8, 12, 11, 31, 32, 36, 35),
(9, 10, 14, 13, 33, 34, 38, 37),
(10, 11, 15, 14, 34, 35, 39, 38),
# (11, 12, 16, 15, 35, 36, 40, 39),
(13, 14, 18, 17, 37, 38, 42, 41),
# (14, 15, 19, 18, 38, 39, 43, 42),
# (15, 16, 20, 19, 39, 40, 44, 43),
(17, 18, 22, 21, 41, 42, 46, 45),
(18, 19, 23, 22, 42, 43, 47, 46),
(19, 20, 24, 23, 43, 44, 48, 47),
),
)
gold_mesh_element_connectivity = (
(
11,
(1, 2, 4, 3, 19, 20, 22, 21),
#
#
(3, 4, 6, 5, 21, 22, 24, 23),
#
#
(5, 6, 9, 8, 23, 24, 27, 26),
(6, 7, 10, 9, 24, 25, 28, 27),
#
(8, 9, 12, 11, 26, 27, 30, 29),
#
#
(11, 12, 16, 15, 29, 30, 34, 33),
(12, 13, 17, 16, 30, 31, 35, 34),
(13, 14, 18, 17, 31, 32, 36, 35),
),
)
class LetterF3D(Example):
"""A three dimensional variation of the letter F, in a non-standard
orientation.
"""
figure_title: str = COMMON_TITLE + "LetterF3D"
file_stem: str = "letter_f_3d"
segmentation = np.array(
[
[
[1, 1, 1, 1],
[1, 1, 1, 1],
[1, 1, 1, 1],
[1, 1, 1, 1],
[1, 1, 1, 1],
],
[
[1, 0, 0, 0],
[1, 0, 0, 0],
[1, 1, 1, 1],
[1, 0, 0, 0],
[1, 1, 1, 1],
],
[
[1, 0, 0, 0],
[1, 0, 0, 0],
[1, 0, 0, 0],
[1, 0, 0, 0],
[1, 1, 1, 1],
],
],
dtype=np.uint8,
)
included_ids = (1,)
gold_lattice = (
(1, 2, 7, 6, 31, 32, 37, 36),
(2, 3, 8, 7, 32, 33, 38, 37),
(3, 4, 9, 8, 33, 34, 39, 38),
(4, 5, 10, 9, 34, 35, 40, 39),
(6, 7, 12, 11, 36, 37, 42, 41),
(7, 8, 13, 12, 37, 38, 43, 42),
(8, 9, 14, 13, 38, 39, 44, 43),
(9, 10, 15, 14, 39, 40, 45, 44),
(11, 12, 17, 16, 41, 42, 47, 46),
(12, 13, 18, 17, 42, 43, 48, 47),
(13, 14, 19, 18, 43, 44, 49, 48),
(14, 15, 20, 19, 44, 45, 50, 49),
(16, 17, 22, 21, 46, 47, 52, 51),
(17, 18, 23, 22, 47, 48, 53, 52),
(18, 19, 24, 23, 48, 49, 54, 53),
(19, 20, 25, 24, 49, 50, 55, 54),
(21, 22, 27, 26, 51, 52, 57, 56),
(22, 23, 28, 27, 52, 53, 58, 57),
(23, 24, 29, 28, 53, 54, 59, 58),
(24, 25, 30, 29, 54, 55, 60, 59),
(31, 32, 37, 36, 61, 62, 67, 66),
(32, 33, 38, 37, 62, 63, 68, 67),
(33, 34, 39, 38, 63, 64, 69, 68),
(34, 35, 40, 39, 64, 65, 70, 69),
(36, 37, 42, 41, 66, 67, 72, 71),
(37, 38, 43, 42, 67, 68, 73, 72),
(38, 39, 44, 43, 68, 69, 74, 73),
(39, 40, 45, 44, 69, 70, 75, 74),
(41, 42, 47, 46, 71, 72, 77, 76),
(42, 43, 48, 47, 72, 73, 78, 77),
(43, 44, 49, 48, 73, 74, 79, 78),
(44, 45, 50, 49, 74, 75, 80, 79),
(46, 47, 52, 51, 76, 77, 82, 81),
(47, 48, 53, 52, 77, 78, 83, 82),
(48, 49, 54, 53, 78, 79, 84, 83),
(49, 50, 55, 54, 79, 80, 85, 84),
(51, 52, 57, 56, 81, 82, 87, 86),
(52, 53, 58, 57, 82, 83, 88, 87),
(53, 54, 59, 58, 83, 84, 89, 88),
(54, 55, 60, 59, 84, 85, 90, 89),
(61, 62, 67, 66, 91, 92, 97, 96),
(62, 63, 68, 67, 92, 93, 98, 97),
(63, 64, 69, 68, 93, 94, 99, 98),
(64, 65, 70, 69, 94, 95, 100, 99),
(66, 67, 72, 71, 96, 97, 102, 101),
(67, 68, 73, 72, 97, 98, 103, 102),
(68, 69, 74, 73, 98, 99, 104, 103),
(69, 70, 75, 74, 99, 100, 105, 104),
(71, 72, 77, 76, 101, 102, 107, 106),
(72, 73, 78, 77, 102, 103, 108, 107),
(73, 74, 79, 78, 103, 104, 109, 108),
(74, 75, 80, 79, 104, 105, 110, 109),
(76, 77, 82, 81, 106, 107, 112, 111),
(77, 78, 83, 82, 107, 108, 113, 112),
(78, 79, 84, 83, 108, 109, 114, 113),
(79, 80, 85, 84, 109, 110, 115, 114),
(81, 82, 87, 86, 111, 112, 117, 116),
(82, 83, 88, 87, 112, 113, 118, 117),
(83, 84, 89, 88, 113, 114, 119, 118),
(84, 85, 90, 89, 114, 115, 120, 119),
)
gold_mesh_lattice_connectivity = (
(
1,
(1, 2, 7, 6, 31, 32, 37, 36),
(2, 3, 8, 7, 32, 33, 38, 37),
(3, 4, 9, 8, 33, 34, 39, 38),
(4, 5, 10, 9, 34, 35, 40, 39),
(6, 7, 12, 11, 36, 37, 42, 41),
(7, 8, 13, 12, 37, 38, 43, 42),
(8, 9, 14, 13, 38, 39, 44, 43),
(9, 10, 15, 14, 39, 40, 45, 44),
(11, 12, 17, 16, 41, 42, 47, 46),
(12, 13, 18, 17, 42, 43, 48, 47),
(13, 14, 19, 18, 43, 44, 49, 48),
(14, 15, 20, 19, 44, 45, 50, 49),
(16, 17, 22, 21, 46, 47, 52, 51),
(17, 18, 23, 22, 47, 48, 53, 52),
(18, 19, 24, 23, 48, 49, 54, 53),
(19, 20, 25, 24, 49, 50, 55, 54),
(21, 22, 27, 26, 51, 52, 57, 56),
(22, 23, 28, 27, 52, 53, 58, 57),
(23, 24, 29, 28, 53, 54, 59, 58),
(24, 25, 30, 29, 54, 55, 60, 59),
(31, 32, 37, 36, 61, 62, 67, 66),
(36, 37, 42, 41, 66, 67, 72, 71),
(41, 42, 47, 46, 71, 72, 77, 76),
(42, 43, 48, 47, 72, 73, 78, 77),
(43, 44, 49, 48, 73, 74, 79, 78),
(44, 45, 50, 49, 74, 75, 80, 79),
(46, 47, 52, 51, 76, 77, 82, 81),
(51, 52, 57, 56, 81, 82, 87, 86),
(52, 53, 58, 57, 82, 83, 88, 87),
(53, 54, 59, 58, 83, 84, 89, 88),
(54, 55, 60, 59, 84, 85, 90, 89),
(61, 62, 67, 66, 91, 92, 97, 96),
(66, 67, 72, 71, 96, 97, 102, 101),
(71, 72, 77, 76, 101, 102, 107, 106),
(76, 77, 82, 81, 106, 107, 112, 111),
(81, 82, 87, 86, 111, 112, 117, 116),
(82, 83, 88, 87, 112, 113, 118, 117),
(83, 84, 89, 88, 113, 114, 119, 118),
(84, 85, 90, 89, 114, 115, 120, 119),
),
)
gold_mesh_element_connectivity = (
(
1,
(1, 2, 7, 6, 31, 32, 37, 36),
(2, 3, 8, 7, 32, 33, 38, 37),
(3, 4, 9, 8, 33, 34, 39, 38),
(4, 5, 10, 9, 34, 35, 40, 39),
(6, 7, 12, 11, 36, 37, 42, 41),
(7, 8, 13, 12, 37, 38, 43, 42),
(8, 9, 14, 13, 38, 39, 44, 43),
(9, 10, 15, 14, 39, 40, 45, 44),
(11, 12, 17, 16, 41, 42, 47, 46),
(12, 13, 18, 17, 42, 43, 48, 47),
(13, 14, 19, 18, 43, 44, 49, 48),
(14, 15, 20, 19, 44, 45, 50, 49),
(16, 17, 22, 21, 46, 47, 52, 51),
(17, 18, 23, 22, 47, 48, 53, 52),
(18, 19, 24, 23, 48, 49, 54, 53),
(19, 20, 25, 24, 49, 50, 55, 54),
(21, 22, 27, 26, 51, 52, 57, 56),
(22, 23, 28, 27, 52, 53, 58, 57),
(23, 24, 29, 28, 53, 54, 59, 58),
(24, 25, 30, 29, 54, 55, 60, 59),
(31, 32, 37, 36, 61, 62, 64, 63),
(36, 37, 42, 41, 63, 64, 66, 65),
(41, 42, 47, 46, 65, 66, 71, 70),
(42, 43, 48, 47, 66, 67, 72, 71),
(43, 44, 49, 48, 67, 68, 73, 72),
(44, 45, 50, 49, 68, 69, 74, 73),
(46, 47, 52, 51, 70, 71, 76, 75),
(51, 52, 57, 56, 75, 76, 81, 80),
(52, 53, 58, 57, 76, 77, 82, 81),
(53, 54, 59, 58, 77, 78, 83, 82),
(54, 55, 60, 59, 78, 79, 84, 83),
(61, 62, 64, 63, 85, 86, 88, 87),
(63, 64, 66, 65, 87, 88, 90, 89),
(65, 66, 71, 70, 89, 90, 92, 91),
(70, 71, 76, 75, 91, 92, 94, 93),
(75, 76, 81, 80, 93, 94, 99, 98),
(76, 77, 82, 81, 94, 95, 100, 99),
(77, 78, 83, 82, 95, 96, 101, 100),
(78, 79, 84, 83, 96, 97, 102, 101),
),
)
class Sparse(Example):
"""A radomized 5x5x5 segmentation."""
figure_title: str = COMMON_TITLE + "Sparse"
file_stem: str = "sparse"
segmentation = np.array(
[
[
[0, 0, 0, 0, 2],
[0, 1, 0, 0, 2],
[1, 2, 0, 2, 0],
[0, 1, 0, 2, 0],
[1, 0, 0, 0, 1],
],
[
[2, 0, 2, 0, 0],
[1, 1, 0, 2, 2],
[2, 0, 0, 0, 0],
[1, 0, 0, 2, 0],
[2, 0, 2, 0, 2],
],
[
[0, 0, 1, 0, 2],
[0, 0, 0, 1, 2],
[0, 0, 2, 2, 2],
[0, 0, 1, 0, 1],
[0, 1, 0, 1, 0],
],
[
[0, 1, 2, 1, 2],
[2, 0, 2, 0, 1],
[1, 2, 2, 0, 0],
[2, 1, 1, 1, 1],
[0, 0, 1, 0, 0],
],
[
[0, 1, 0, 2, 0],
[1, 0, 0, 0, 2],
[0, 1, 0, 0, 0],
[1, 0, 0, 0, 0],
[0, 0, 1, 2, 1],
],
],
dtype=np.uint8,
)
included_ids = (
1,
2,
)
gold_lattice = (
(1, 2, 8, 7, 37, 38, 44, 43),
(2, 3, 9, 8, 38, 39, 45, 44),
(3, 4, 10, 9, 39, 40, 46, 45),
(4, 5, 11, 10, 40, 41, 47, 46),
(5, 6, 12, 11, 41, 42, 48, 47),
(7, 8, 14, 13, 43, 44, 50, 49),
(8, 9, 15, 14, 44, 45, 51, 50),
(9, 10, 16, 15, 45, 46, 52, 51),
(10, 11, 17, 16, 46, 47, 53, 52),
(11, 12, 18, 17, 47, 48, 54, 53),
(13, 14, 20, 19, 49, 50, 56, 55),
(14, 15, 21, 20, 50, 51, 57, 56),
(15, 16, 22, 21, 51, 52, 58, 57),
(16, 17, 23, 22, 52, 53, 59, 58),
(17, 18, 24, 23, 53, 54, 60, 59),
(19, 20, 26, 25, 55, 56, 62, 61),
(20, 21, 27, 26, 56, 57, 63, 62),
(21, 22, 28, 27, 57, 58, 64, 63),
(22, 23, 29, 28, 58, 59, 65, 64),
(23, 24, 30, 29, 59, 60, 66, 65),
(25, 26, 32, 31, 61, 62, 68, 67),
(26, 27, 33, 32, 62, 63, 69, 68),
(27, 28, 34, 33, 63, 64, 70, 69),
(28, 29, 35, 34, 64, 65, 71, 70),
(29, 30, 36, 35, 65, 66, 72, 71),
(37, 38, 44, 43, 73, 74, 80, 79),
(38, 39, 45, 44, 74, 75, 81, 80),
(39, 40, 46, 45, 75, 76, 82, 81),
(40, 41, 47, 46, 76, 77, 83, 82),
(41, 42, 48, 47, 77, 78, 84, 83),
(43, 44, 50, 49, 79, 80, 86, 85),
(44, 45, 51, 50, 80, 81, 87, 86),
(45, 46, 52, 51, 81, 82, 88, 87),
(46, 47, 53, 52, 82, 83, 89, 88),
(47, 48, 54, 53, 83, 84, 90, 89),
(49, 50, 56, 55, 85, 86, 92, 91),
(50, 51, 57, 56, 86, 87, 93, 92),
(51, 52, 58, 57, 87, 88, 94, 93),
(52, 53, 59, 58, 88, 89, 95, 94),
(53, 54, 60, 59, 89, 90, 96, 95),
(55, 56, 62, 61, 91, 92, 98, 97),
(56, 57, 63, 62, 92, 93, 99, 98),
(57, 58, 64, 63, 93, 94, 100, 99),
(58, 59, 65, 64, 94, 95, 101, 100),
(59, 60, 66, 65, 95, 96, 102, 101),
(61, 62, 68, 67, 97, 98, 104, 103),
(62, 63, 69, 68, 98, 99, 105, 104),
(63, 64, 70, 69, 99, 100, 106, 105),
(64, 65, 71, 70, 100, 101, 107, 106),
(65, 66, 72, 71, 101, 102, 108, 107),
(73, 74, 80, 79, 109, 110, 116, 115),
(74, 75, 81, 80, 110, 111, 117, 116),
(75, 76, 82, 81, 111, 112, 118, 117),
(76, 77, 83, 82, 112, 113, 119, 118),
(77, 78, 84, 83, 113, 114, 120, 119),
(79, 80, 86, 85, 115, 116, 122, 121),
(80, 81, 87, 86, 116, 117, 123, 122),
(81, 82, 88, 87, 117, 118, 124, 123),
(82, 83, 89, 88, 118, 119, 125, 124),
(83, 84, 90, 89, 119, 120, 126, 125),
(85, 86, 92, 91, 121, 122, 128, 127),
(86, 87, 93, 92, 122, 123, 129, 128),
(87, 88, 94, 93, 123, 124, 130, 129),
(88, 89, 95, 94, 124, 125, 131, 130),
(89, 90, 96, 95, 125, 126, 132, 131),
(91, 92, 98, 97, 127, 128, 134, 133),
(92, 93, 99, 98, 128, 129, 135, 134),
(93, 94, 100, 99, 129, 130, 136, 135),
(94, 95, 101, 100, 130, 131, 137, 136),
(95, 96, 102, 101, 131, 132, 138, 137),
(97, 98, 104, 103, 133, 134, 140, 139),
(98, 99, 105, 104, 134, 135, 141, 140),
(99, 100, 106, 105, 135, 136, 142, 141),
(100, 101, 107, 106, 136, 137, 143, 142),
(101, 102, 108, 107, 137, 138, 144, 143),
(109, 110, 116, 115, 145, 146, 152, 151),
(110, 111, 117, 116, 146, 147, 153, 152),
(111, 112, 118, 117, 147, 148, 154, 153),
(112, 113, 119, 118, 148, 149, 155, 154),
(113, 114, 120, 119, 149, 150, 156, 155),
(115, 116, 122, 121, 151, 152, 158, 157),
(116, 117, 123, 122, 152, 153, 159, 158),
(117, 118, 124, 123, 153, 154, 160, 159),
(118, 119, 125, 124, 154, 155, 161, 160),
(119, 120, 126, 125, 155, 156, 162, 161),
(121, 122, 128, 127, 157, 158, 164, 163),
(122, 123, 129, 128, 158, 159, 165, 164),
(123, 124, 130, 129, 159, 160, 166, 165),
(124, 125, 131, 130, 160, 161, 167, 166),
(125, 126, 132, 131, 161, 162, 168, 167),
(127, 128, 134, 133, 163, 164, 170, 169),
(128, 129, 135, 134, 164, 165, 171, 170),
(129, 130, 136, 135, 165, 166, 172, 171),
(130, 131, 137, 136, 166, 167, 173, 172),
(131, 132, 138, 137, 167, 168, 174, 173),
(133, 134, 140, 139, 169, 170, 176, 175),
(134, 135, 141, 140, 170, 171, 177, 176),
(135, 136, 142, 141, 171, 172, 178, 177),
(136, 137, 143, 142, 172, 173, 179, 178),
(137, 138, 144, 143, 173, 174, 180, 179),
(145, 146, 152, 151, 181, 182, 188, 187),
(146, 147, 153, 152, 182, 183, 189, 188),
(147, 148, 154, 153, 183, 184, 190, 189),
(148, 149, 155, 154, 184, 185, 191, 190),
(149, 150, 156, 155, 185, 186, 192, 191),
(151, 152, 158, 157, 187, 188, 194, 193),
(152, 153, 159, 158, 188, 189, 195, 194),
(153, 154, 160, 159, 189, 190, 196, 195),
(154, 155, 161, 160, 190, 191, 197, 196),
(155, 156, 162, 161, 191, 192, 198, 197),
(157, 158, 164, 163, 193, 194, 200, 199),
(158, 159, 165, 164, 194, 195, 201, 200),
(159, 160, 166, 165, 195, 196, 202, 201),
(160, 161, 167, 166, 196, 197, 203, 202),
(161, 162, 168, 167, 197, 198, 204, 203),
(163, 164, 170, 169, 199, 200, 206, 205),
(164, 165, 171, 170, 200, 201, 207, 206),
(165, 166, 172, 171, 201, 202, 208, 207),
(166, 167, 173, 172, 202, 203, 209, 208),
(167, 168, 174, 173, 203, 204, 210, 209),
(169, 170, 176, 175, 205, 206, 212, 211),
(170, 171, 177, 176, 206, 207, 213, 212),
(171, 172, 178, 177, 207, 208, 214, 213),
(172, 173, 179, 178, 208, 209, 215, 214),
(173, 174, 180, 179, 209, 210, 216, 215),
)
gold_mesh_lattice_connectivity = (
(
1,
(8, 9, 15, 14, 44, 45, 51, 50),
(13, 14, 20, 19, 49, 50, 56, 55),
(20, 21, 27, 26, 56, 57, 63, 62),
(25, 26, 32, 31, 61, 62, 68, 67),
(29, 30, 36, 35, 65, 66, 72, 71),
(43, 44, 50, 49, 79, 80, 86, 85),
(44, 45, 51, 50, 80, 81, 87, 86),
(55, 56, 62, 61, 91, 92, 98, 97),
(75, 76, 82, 81, 111, 112, 118, 117),
(82, 83, 89, 88, 118, 119, 125, 124),
(93, 94, 100, 99, 129, 130, 136, 135),
(95, 96, 102, 101, 131, 132, 138, 137),
(98, 99, 105, 104, 134, 135, 141, 140),
(100, 101, 107, 106, 136, 137, 143, 142),
(110, 111, 117, 116, 146, 147, 153, 152),
(112, 113, 119, 118, 148, 149, 155, 154),
(119, 120, 126, 125, 155, 156, 162, 161),
(121, 122, 128, 127, 157, 158, 164, 163),
(128, 129, 135, 134, 164, 165, 171, 170),
(129, 130, 136, 135, 165, 166, 172, 171),
(130, 131, 137, 136, 166, 167, 173, 172),
(131, 132, 138, 137, 167, 168, 174, 173),
(135, 136, 142, 141, 171, 172, 178, 177),
(146, 147, 153, 152, 182, 183, 189, 188),
(151, 152, 158, 157, 187, 188, 194, 193),
(158, 159, 165, 164, 194, 195, 201, 200),
(163, 164, 170, 169, 199, 200, 206, 205),
(171, 172, 178, 177, 207, 208, 214, 213),
(173, 174, 180, 179, 209, 210, 216, 215),
),
(
2,
(5, 6, 12, 11, 41, 42, 48, 47),
(11, 12, 18, 17, 47, 48, 54, 53),
(14, 15, 21, 20, 50, 51, 57, 56),
(16, 17, 23, 22, 52, 53, 59, 58),
(22, 23, 29, 28, 58, 59, 65, 64),
(37, 38, 44, 43, 73, 74, 80, 79),
(39, 40, 46, 45, 75, 76, 82, 81),
(46, 47, 53, 52, 82, 83, 89, 88),
(47, 48, 54, 53, 83, 84, 90, 89),
(49, 50, 56, 55, 85, 86, 92, 91),
(58, 59, 65, 64, 94, 95, 101, 100),
(61, 62, 68, 67, 97, 98, 104, 103),
(63, 64, 70, 69, 99, 100, 106, 105),
(65, 66, 72, 71, 101, 102, 108, 107),
(77, 78, 84, 83, 113, 114, 120, 119),
(83, 84, 90, 89, 119, 120, 126, 125),
(87, 88, 94, 93, 123, 124, 130, 129),
(88, 89, 95, 94, 124, 125, 131, 130),
(89, 90, 96, 95, 125, 126, 132, 131),
(111, 112, 118, 117, 147, 148, 154, 153),
(113, 114, 120, 119, 149, 150, 156, 155),
(115, 116, 122, 121, 151, 152, 158, 157),
(117, 118, 124, 123, 153, 154, 160, 159),
(122, 123, 129, 128, 158, 159, 165, 164),
(123, 124, 130, 129, 159, 160, 166, 165),
(127, 128, 134, 133, 163, 164, 170, 169),
(148, 149, 155, 154, 184, 185, 191, 190),
(155, 156, 162, 161, 191, 192, 198, 197),
(172, 173, 179, 178, 208, 209, 215, 214),
),
)
gold_mesh_element_connectivity = (
(
1,
(3, 4, 9, 8, 35, 36, 42, 41),
(7, 8, 14, 13, 40, 41, 47, 46),
(14, 15, 20, 19, 47, 48, 53, 52),
(18, 19, 25, 24, 51, 52, 58, 57),
(22, 23, 27, 26, 55, 56, 62, 61),
(34, 35, 41, 40, 69, 70, 76, 75),
(35, 36, 42, 41, 70, 71, 77, 76),
(46, 47, 52, 51, 81, 82, 88, 87),
(65, 66, 72, 71, 100, 101, 107, 106),
(72, 73, 79, 78, 107, 108, 114, 113),
(83, 84, 90, 89, 118, 119, 125, 124),
(85, 86, 92, 91, 120, 121, 127, 126),
(88, 89, 95, 94, 123, 124, 129, 128),
(90, 91, 97, 96, 125, 126, 131, 130),
(99, 100, 106, 105, 132, 133, 139, 138),
(101, 102, 108, 107, 134, 135, 141, 140),
(108, 109, 115, 114, 141, 142, 148, 147),
(110, 111, 117, 116, 143, 144, 150, 149),
(117, 118, 124, 123, 150, 151, 157, 156),
(118, 119, 125, 124, 151, 152, 158, 157),
(119, 120, 126, 125, 152, 153, 159, 158),
(120, 121, 127, 126, 153, 154, 160, 159),
(124, 125, 130, 129, 157, 158, 162, 161),
(132, 133, 139, 138, 165, 166, 171, 170),
(137, 138, 144, 143, 169, 170, 176, 175),
(144, 145, 151, 150, 176, 177, 182, 181),
(149, 150, 156, 155, 180, 181, 184, 183),
(157, 158, 162, 161, 185, 186, 190, 189),
(159, 160, 164, 163, 187, 188, 192, 191),
),
(
2,
(1, 2, 6, 5, 32, 33, 39, 38),
(5, 6, 12, 11, 38, 39, 45, 44),
(8, 9, 15, 14, 41, 42, 48, 47),
(10, 11, 17, 16, 43, 44, 50, 49),
(16, 17, 22, 21, 49, 50, 55, 54),
(28, 29, 35, 34, 63, 64, 70, 69),
(30, 31, 37, 36, 65, 66, 72, 71),
(37, 38, 44, 43, 72, 73, 79, 78),
(38, 39, 45, 44, 73, 74, 80, 79),
(40, 41, 47, 46, 75, 76, 82, 81),
(49, 50, 55, 54, 84, 85, 91, 90),
(51, 52, 58, 57, 87, 88, 94, 93),
(53, 54, 60, 59, 89, 90, 96, 95),
(55, 56, 62, 61, 91, 92, 98, 97),
(67, 68, 74, 73, 102, 103, 109, 108),
(73, 74, 80, 79, 108, 109, 115, 114),
(77, 78, 84, 83, 112, 113, 119, 118),
(78, 79, 85, 84, 113, 114, 120, 119),
(79, 80, 86, 85, 114, 115, 121, 120),
(100, 101, 107, 106, 133, 134, 140, 139),
(102, 103, 109, 108, 135, 136, 142, 141),
(104, 105, 111, 110, 137, 138, 144, 143),
(106, 107, 113, 112, 139, 140, 146, 145),
(111, 112, 118, 117, 144, 145, 151, 150),
(112, 113, 119, 118, 145, 146, 152, 151),
(116, 117, 123, 122, 149, 150, 156, 155),
(134, 135, 141, 140, 167, 168, 173, 172),
(141, 142, 148, 147, 173, 174, 179, 178),
(158, 159, 163, 162, 186, 187, 191, 190),
),
)
examples_figures.py
r"""This module, examples_figures.py, demonstrates creating a pixel slice in
the (x, y) plane, and then appending layers in the z axis, to create a 3D
voxel lattice, as a precursor for a hexahedral finite element mesh.
Example
-------
source ~/autotwin/automesh/.venv/bin/activate
pip install matplotlib
cd ~/autotwin/automesh/book/examples/unit_tests
python examples_figures.py
Ouputk
-----
The `output_npy` segmentation data files
The `output_png` visualization files
"""
# standard library
import datetime
from pathlib import Path
from typing import Final
# third-party libary
import matplotlib.pyplot as plt
from matplotlib.colors import LightSource
import numpy as np
from numpy.typing import NDArray
import examples_types as types
import examples_data as data
# Type aliases
Example = types.Example
def lattice_connectivity(ex: Example) -> NDArray[np.uint8]:
"""Given an Example, prints the lattice connectivity."""
offset = 0
nz, ny, nx = ex.segmentation.shape
nzp, nyp, nxp = nz + 1, ny + 1, nx + 1
# Generate the lattice nodes
lattice_nodes = []
lattice_node = 0
for k in range(nzp):
for j in range(nyp):
for i in range(nxp):
lattice_node += 1
lattice_nodes.append([lattice_node, i, j, k])
# connectivity for each voxel
cvs = []
offset = 0
# print("processing indices...")
for iz in range(nz):
for iy in range(ny):
for ix in range(nx):
# print(f"(ix, iy, iz) = ({ix}, {iy}, {iz})")
cv = offset + np.array(
[
(iz + 0) * (nxp * nyp) + (iy + 0) * nxp + ix + 1,
(iz + 0) * (nxp * nyp) + (iy + 0) * nxp + ix + 2,
(iz + 0) * (nxp * nyp) + (iy + 1) * nxp + ix + 2,
(iz + 0) * (nxp * nyp) + (iy + 1) * nxp + ix + 1,
(iz + 1) * (nxp * nyp) + (iy + 0) * nxp + ix + 1,
(iz + 1) * (nxp * nyp) + (iy + 0) * nxp + ix + 2,
(iz + 1) * (nxp * nyp) + (iy + 1) * nxp + ix + 2,
(iz + 1) * (nxp * nyp) + (iy + 1) * nxp + ix + 1,
]
)
cvs.append(cv)
cs = np.vstack(cvs)
# voxel by voxel comparison
# breakpoint()
vv = ex.gold_lattice == cs
assert np.all(vv)
return cs
def mesh_lattice_connectivity(
ex: Example,
lattice: np.ndarray,
) -> tuple:
"""Given an Example (in particular, the Example's voxel data structure,
a segmentation) and the `lattice_connectivity`, create the connectivity
for the mesh with lattice node numbers. A voxel with a segmentation id not
in the Example's included ids tuple is excluded from the mesh.
"""
# segmentation = ex.segmentation.flatten().squeeze()
segmentation = ex.segmentation.flatten()
# breakpoint()
# assert that the list of included ids is equal
included_set_unordered = set(ex.included_ids)
included_list_ordered = sorted(included_set_unordered)
# breakpoint()
seg_set = set(segmentation)
for item in included_list_ordered:
assert item in seg_set, (
f"Error: `included_ids` item {item} is not in the segmentation"
)
# Create a list of finite elements from the lattice elements. If the
# lattice element has a segmentation id that is not in the included_ids,
# exlude the voxel element from the collected list to create the finite
# element list
blocks = () # empty tuple
# breakpoint()
for bb in included_list_ordered:
# included_elements = []
elements = () # empty tuple
elements = elements + (bb,) # insert the block number
for i, element in enumerate(lattice):
if bb == segmentation[i]:
# breakpoint()
elements = elements + (tuple(element.tolist()),) # overwrite
blocks = blocks + (elements,) # overwrite
# breakpoint()
# return np.array(blocks)
return blocks
def renumber(source: tuple, old: tuple, new: tuple) -> tuple:
"""Given a source tuple, composed of a list of positive integers,
a tuple of `old` numbers that maps into `new` numbers, return the
source tuple with the `new` numbers."""
# the old and the new tuples musts have the same length
err = "Tuples `old` and `new` must have equal length."
assert len(old) == len(new), err
result = ()
for item in source:
idx = old.index(item)
new_value = new[idx]
result = result + (new_value,)
return result
def mesh_element_connectivity(mesh_with_lattice_connectivity: tuple):
"""Given a mesh with lattice connectivity, return a mesh with finite
element connectivity.
"""
# create a list of unordered lattice node numbers
ln = []
for item in mesh_with_lattice_connectivity:
# print(f"item is {item}")
# The first item is the block number
# block = item[0]
# The second and onward items are the elements
elements = item[1:]
for element in elements:
ln += list(element)
ln_set = set(ln) # sets are not necessarily ordered
ln_ordered = tuple(sorted(ln_set)) # now these unique integers are ordered
# and they will map into the new compressed unique interger list `mapsto`
mapsto = tuple(range(1, len(ln_ordered) + 1))
# now build a mesh_with_element_connectivity
mesh = () # empty tuple
# breakpoint()
for item in mesh_with_lattice_connectivity:
# The first item is the block number
block_number = item[0]
block_and_elements = () # empty tuple
# insert the block number
block_and_elements = block_and_elements + (block_number,)
for element in item[1:]:
new_element = renumber(source=element, old=ln_ordered, new=mapsto)
# overwrite
block_and_elements = block_and_elements + (new_element,)
mesh = mesh + (block_and_elements,) # overwrite
return mesh
def flatten_tuple(t):
"""Uses recursion to convert nested tuples into a single-sevel tuple.
Example:
nested_tuple = (1, (2, 3), (4, (5, 6)), 7)
flattened_tuple = flatten_tuple(nested_tuple)
print(flattened_tuple) # Output: (1, 2, 3, 4, 5, 6, 7)
"""
flat_list = []
for item in t:
if isinstance(item, tuple):
flat_list.extend(flatten_tuple(item))
else:
flat_list.append(item)
# breakpoint()
return tuple(flat_list)
def elements_without_block_ids(mesh: tuple) -> tuple:
"""Given a mesh, removes the block ids and returns only just the
element connectivities.
"""
aa = ()
for item in mesh:
bb = item[1:]
aa = aa + bb
return aa
def main():
"""The main program."""
# Create an instance of a specific example
# user input begin
examples = [
data.Single(),
# data.DoubleX(),
# data.DoubleY(),
# data.TripleX(),
# data.QuadrupleX(),
# data.Quadruple2VoidsX(),
# data.Quadruple2Blocks(),
# data.Quadruple2BlocksVoid(),
# data.Cube(),
# data.CubeMulti(),
# data.CubeWithInclusion(),
data.Bracket(),
# data.LetterF(),
# data.LetterF3D(),
# data.Sparse(),
]
# output_dir: Final[str] = "~/scratch"
output_dir: Final[Path] = Path(__file__).parent
DPI: Final[int] = 300 # resolution, dots per inch
for ex in examples:
# computation
output_npy: Path = Path(output_dir).expanduser().joinpath(ex.file_stem + ".npy")
# visualization
SHOW: Final[bool] = True # Post-processing visuals, show on screen
SAVE: Final[bool] = True # Save the .png file
output_png_short = ex.file_stem + ".png"
output_png: Path = Path(output_dir).expanduser().joinpath(output_png_short)
# el, az, roll = 25, -115, 0
# el, az, roll = 28, -115, 0
el, az, roll = 63, -110, 0 # used for most visuals
# el, az, roll = 11, -111, 0 # used for CubeWithInclusion
# el, az, roll = 60, -121, 0
# el, az, roll = 42, -120, 0
#
# colors
# cmap = cm.get_cmap("viridis") # viridis colormap
# cmap = plt.get_cmap(name="viridis")
cmap = plt.get_cmap(name="tab10")
# number of discrete colors
num_colors = len(ex.included_ids)
colors = cmap(np.linspace(0, 1, num_colors))
# breakpoint()
# azimuth (deg):
# 0 is east (from +y-axis looking back toward origin)
# 90 is north (from +x-axis looking back toward origin)
# 180 is west (from -y-axis looking back toward origin)
# 270 is south (from -x-axis looking back toward origin)
# elevation (deg): 0 is horizontal, 90 is vertical (+z-axis up)
lightsource = LightSource(azdeg=325, altdeg=45) # azimuth, elevation
nodes_shown: bool = True
# nodes_shown: bool = False
voxel_alpha: float = 0.1
# voxel_alpha: float = 0.7
# io: if the output directory does not already exist, create it
output_path = Path(output_dir).expanduser()
if not output_path.exists():
print(f"Could not find existing output directory: {output_path}")
Path.mkdir(output_path)
print(f"Created: {output_path}")
assert output_path.exists()
nelz, nely, nelx = ex.segmentation.shape
lc = lattice_connectivity(ex=ex)
# breakpoint()
mesh_w_lattice_conn = mesh_lattice_connectivity(ex=ex, lattice=lc)
err = "Calculated lattice connectivity error."
assert mesh_w_lattice_conn == ex.gold_mesh_lattice_connectivity, err
mesh_w_element_conn = mesh_element_connectivity(mesh_w_lattice_conn)
err = "Calcualted element connectivity error." # overwrite
assert mesh_w_element_conn == ex.gold_mesh_element_connectivity, err
# save the numpy data as a .npy file
np.save(output_npy, ex.segmentation)
print(f"Saved: {output_npy}")
# to load the array back from the .npy file,
# use the numpy.load function:
loaded_array = np.load(output_npy)
# verify the loaded array
# print(f"segmentation loaded from saved file: {loaded_array}")
assert np.all(loaded_array == ex.segmentation)
# now that the .npy file has been created and verified,
# move it to the repo at ~/autotwin/automesh/tests/input
if not SHOW:
return
# visualization
# Define the dimensions of the lattice
nxp, nyp, nzp = (nelx + 1, nely + 1, nelz + 1)
# Create a figure and a 3D axis
# fig = plt.figure()
fig = plt.figure(figsize=(10, 5)) # Adjust the figure size
# fig = plt.figure(figsize=(8, 4)) # Adjust the figure size
# ax = fig.add_subplot(111, projection="3d")
# figure with 1 row, 2 columns
ax = fig.add_subplot(1, 2, 1, projection="3d") # r1, c2, 1st subplot
ax2 = fig.add_subplot(1, 2, 2, projection="3d") # r1, c2, 2nd subplot
# For 3D plotting of voxels in matplotlib, we must swap the 'x' and the
# 'z' axes. The original axes in the segmentation are (z, y, x) and
# are numbered (0, 1, 2). We want new exists as (x, y, z) and thus
# with numbering (2, 1, 0).
vox = np.transpose(ex.segmentation, (2, 1, 0))
# add voxels for each of the included materials
for i, block_id in enumerate(ex.included_ids):
# breakpoint()
solid = vox == block_id
# ax.voxels(solid, facecolors=voxel_color, alpha=voxel_alpha)
# ax.voxels(solid, facecolors=colors[i], alpha=voxel_alpha)
ax.voxels(
solid,
facecolors=colors[i],
edgecolor=colors[i],
alpha=voxel_alpha,
lightsource=lightsource,
)
# plot the same voxels on the 2nd axis
ax2.voxels(
solid,
facecolors=colors[i],
edgecolor=colors[i],
alpha=voxel_alpha,
lightsource=lightsource,
)
# breakpoint()
# Generate the lattice points
x = []
y = []
z = []
labels = []
# Generate the element points
xel = []
yel = []
zel = []
# generate a set from the element connectivity
# breakpoint()
# ec_set = set(flatten_tuple(mesh_w_lattice_conn)) # bug!
# bug fix:
ec_set = set(flatten_tuple(elements_without_block_ids(mesh_w_lattice_conn)))
# breakpoint()
lattice_ijk = 0
# gnn = global node number
gnn = 0
gnn_labels = []
for k in range(nzp):
for j in range(nyp):
for i in range(nxp):
x.append(i)
y.append(j)
z.append(k)
if lattice_ijk + 1 in ec_set:
gnn += 1
xel.append(i)
yel.append(j)
zel.append(k)
gnn_labels.append(f" {gnn}")
lattice_ijk += 1
labels.append(f" {lattice_ijk}: ({i},{j},{k})")
if nodes_shown:
# Plot the lattice coordinates
ax.scatter(
x,
y,
z,
s=20,
facecolors="red",
edgecolors="none",
)
# Label the lattice coordinates
for n, label in enumerate(labels):
ax.text(x[n], y[n], z[n], label, color="darkgray", fontsize=8)
# Plot the nodes included in the finite element connectivity
ax2.scatter(
xel,
yel,
zel,
s=30,
facecolors="blue",
edgecolors="blue",
)
# Label the global node numbers
for n, label in enumerate(gnn_labels):
ax2.text(xel[n], yel[n], zel[n], label, color="darkblue", fontsize=8)
# Set labels for the axes
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("z")
# repeat for the 2nd axis
ax2.set_xlabel("x")
ax2.set_ylabel("y")
ax2.set_zlabel("z")
x_ticks = list(range(nxp))
y_ticks = list(range(nyp))
z_ticks = list(range(nzp))
ax.set_xticks(x_ticks)
ax.set_yticks(y_ticks)
ax.set_zticks(z_ticks)
# repeat for the 2nd axis
ax2.set_xticks(x_ticks)
ax2.set_yticks(y_ticks)
ax2.set_zticks(z_ticks)
ax.set_xlim(float(x_ticks[0]), float(x_ticks[-1]))
ax.set_ylim(float(y_ticks[0]), float(y_ticks[-1]))
ax.set_zlim(float(z_ticks[0]), float(z_ticks[-1]))
# repeat for the 2nd axis
ax2.set_xlim(float(x_ticks[0]), float(x_ticks[-1]))
ax2.set_ylim(float(y_ticks[0]), float(y_ticks[-1]))
ax2.set_zlim(float(z_ticks[0]), float(z_ticks[-1]))
# Set the camera view
ax.set_aspect("equal")
ax.view_init(elev=el, azim=az, roll=roll)
# repeat for the 2nd axis
ax2.set_aspect("equal")
ax2.view_init(elev=el, azim=az, roll=roll)
# Adjust the distance of the camera. The default value is 10.
# Increasing/decreasing this value will zoom in/out, respectively.
# ax.dist = 5 # Change the distance of the camera
# Doesn't seem to work, and the title is clipping the uppermost node
# and lattice numbers, so suppress the titles for now.
# Set the title
# ax.set_title(ex.figure_title)
# Add a footnote
# Get the current date and time in UTC
now_utc = datetime.datetime.now(datetime.UTC)
# Format the date and time as a string
timestamp_utc = now_utc.strftime("%Y-%m-%d %H:%M:%S UTC")
fn = f"Figure: {output_png_short} "
fn += f"created with {__file__}\non {timestamp_utc}."
fig.text(0.5, 0.01, fn, ha="center", fontsize=8)
# Show the plot
if SHOW:
plt.show()
if SAVE:
# plt.show()
fig.savefig(output_png, dpi=DPI)
print(f"Saved: {output_png}")
if __name__ == "__main__":
main()
examples_test.py
r"""This module, examples_test.py, tests functionality of the included module.
Example
-------
source ~/autotwin/automesh/.venv/bin/activate
cd ~/autotwin/automesh/book/examples/unit_tests
python -m pytest examples_test.py -v # -v is for verbose
to run a single test in this module, for example `test_hello` function:
python -m pytest examples_test.py::test_foo -v
"""
import pytest
import examples_figures as ff
def test_renumber():
"""Tests that the renumber function works as expected."""
source = (300, 22, 1)
old = (1, 22, 300, 40)
new = (42, 2, 9, 1000)
result = ff.renumber(source=source, old=old, new=new)
assert result == (9, 2, 42)
# Assure that tuples old and new of unequal length raise an AssertionError
new = (42, 2) # overwrite
err = "Tuples `old` and `new` must have equal length."
with pytest.raises(AssertionError, match=err):
_ = ff.renumber(source=source, old=old, new=new)
def test_mesh_with_element_connectivity():
"""Test CubeMulti by hand."""
gold_mesh_lattice_connectivity = (
(
2,
(2, 3, 6, 5, 11, 12, 15, 14),
(4, 5, 8, 7, 13, 14, 17, 16),
(5, 6, 9, 8, 14, 15, 18, 17),
),
(
31,
(11, 12, 15, 14, 20, 21, 24, 23),
),
(
44,
(14, 15, 18, 17, 23, 24, 27, 26),
),
(
82,
(1, 2, 5, 4, 10, 11, 14, 13),
),
)
gold_mesh_element_connectivity = (
(
2,
(2, 3, 6, 5, 11, 12, 15, 14),
(4, 5, 8, 7, 13, 14, 17, 16),
(5, 6, 9, 8, 14, 15, 18, 17),
),
(31, (11, 12, 15, 14, 19, 20, 22, 21)),
(44, (14, 15, 18, 17, 21, 22, 24, 23)),
(82, (1, 2, 5, 4, 10, 11, 14, 13)),
)
result = ff.mesh_element_connectivity(
mesh_with_lattice_connectivity=gold_mesh_lattice_connectivity
)
assert result == gold_mesh_element_connectivity
def test_elements_no_block_ids():
"""Given a mesh, strips the block ids from the"""
known_input = (
(
2,
(2, 3, 6, 5, 11, 12, 15, 14),
(4, 5, 8, 7, 13, 14, 17, 16),
(5, 6, 9, 8, 14, 15, 18, 17),
),
(31, (11, 12, 15, 14, 20, 21, 24, 23)),
(44, (14, 15, 18, 17, 23, 24, 27, 26)),
(82, (1, 2, 5, 4, 10, 11, 14, 13)),
)
gold_output = (
(2, 3, 6, 5, 11, 12, 15, 14),
(4, 5, 8, 7, 13, 14, 17, 16),
(5, 6, 9, 8, 14, 15, 18, 17),
(11, 12, 15, 14, 20, 21, 24, 23),
(14, 15, 18, 17, 23, 24, 27, 26),
(1, 2, 5, 4, 10, 11, 14, 13),
)
result = ff.elements_without_block_ids(mesh=known_input)
assert result == gold_output
examples_types.py
r"""This module, examples_types.py, defines types used
for unit test examples.
"""
from typing import NamedTuple
import numpy as np
class Example(NamedTuple):
"""A base class that has all of the fields required to specialize into a
specific example."""
figure_title: str = "Figure Title"
file_stem: str = "filename"
segmentation = np.array(
[
[
[
1,
],
],
],
dtype=np.uint8,
)
included_ids = (1,)
gold_lattice = None
gold_mesh_lattice_connectivity = None
gold_mesh_element_connectivity = None