Dualization

Dualization is the process of using a primal mesh to construct a dual mesh. Dualization can be performed on 2D/3D surface meshes composed of quadrilateral elements, and 3D volumetric meshes composed of hexahedral elements. Both quadrilateral and hexahedral elements will be discussed.

Quadtree

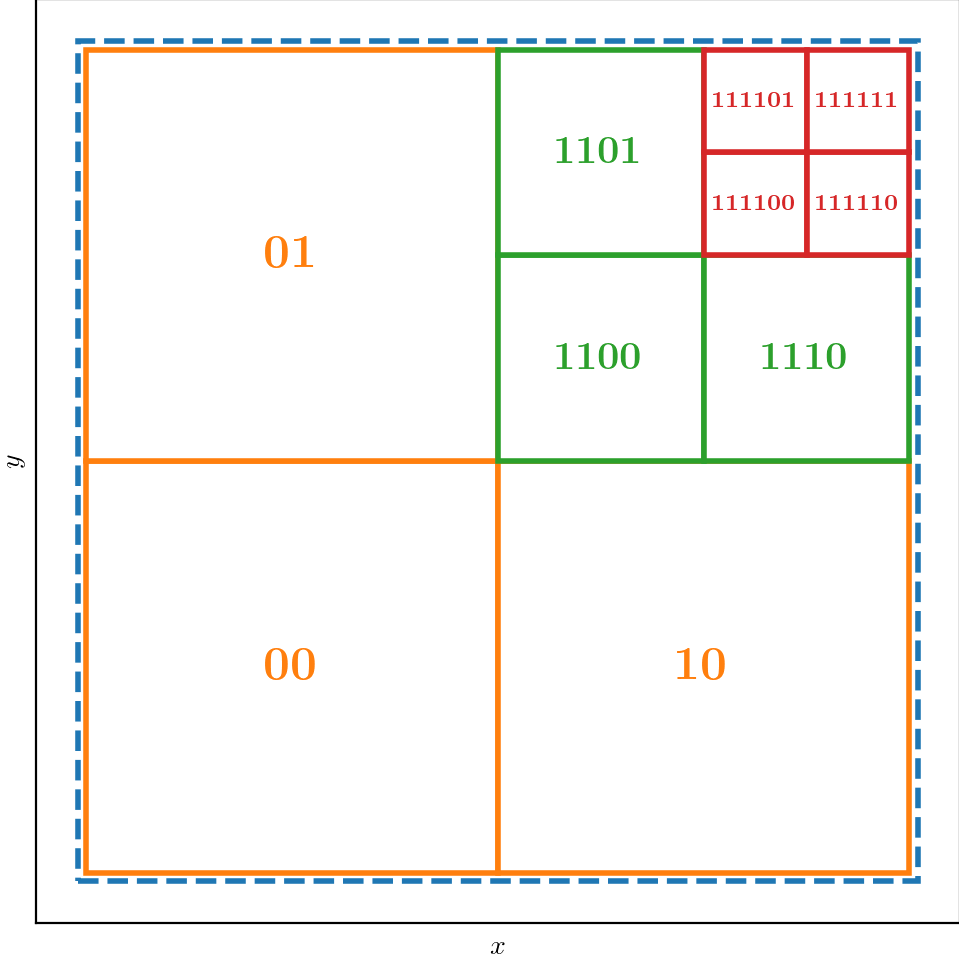
With plot_quadtree_convention.py, we create the following index scheme:

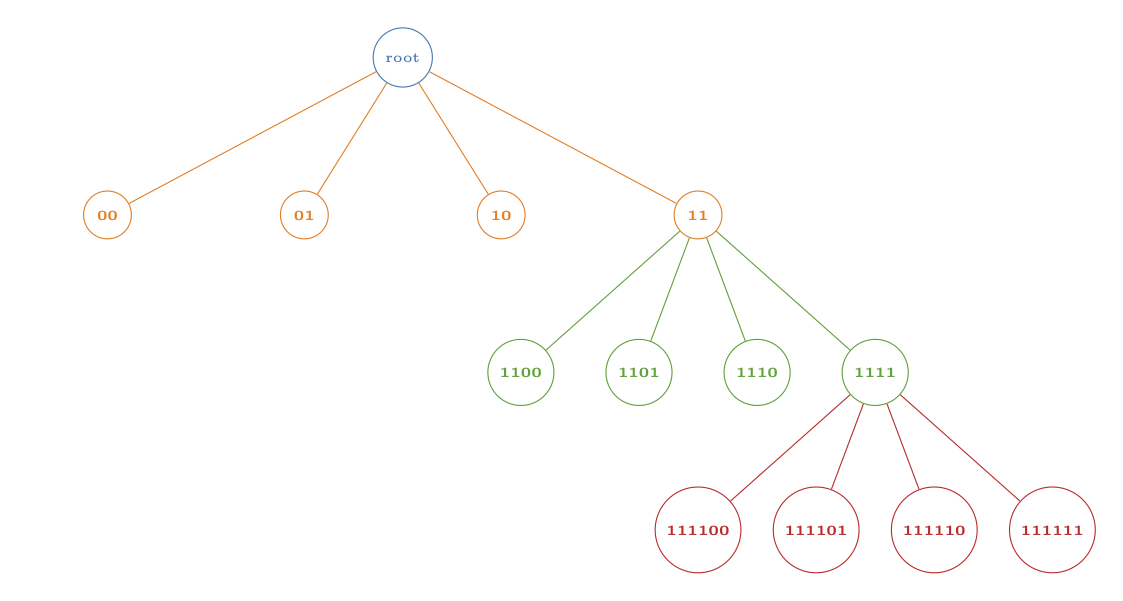
With fig_quadtree.tex, we create the following image of the inverted tree:

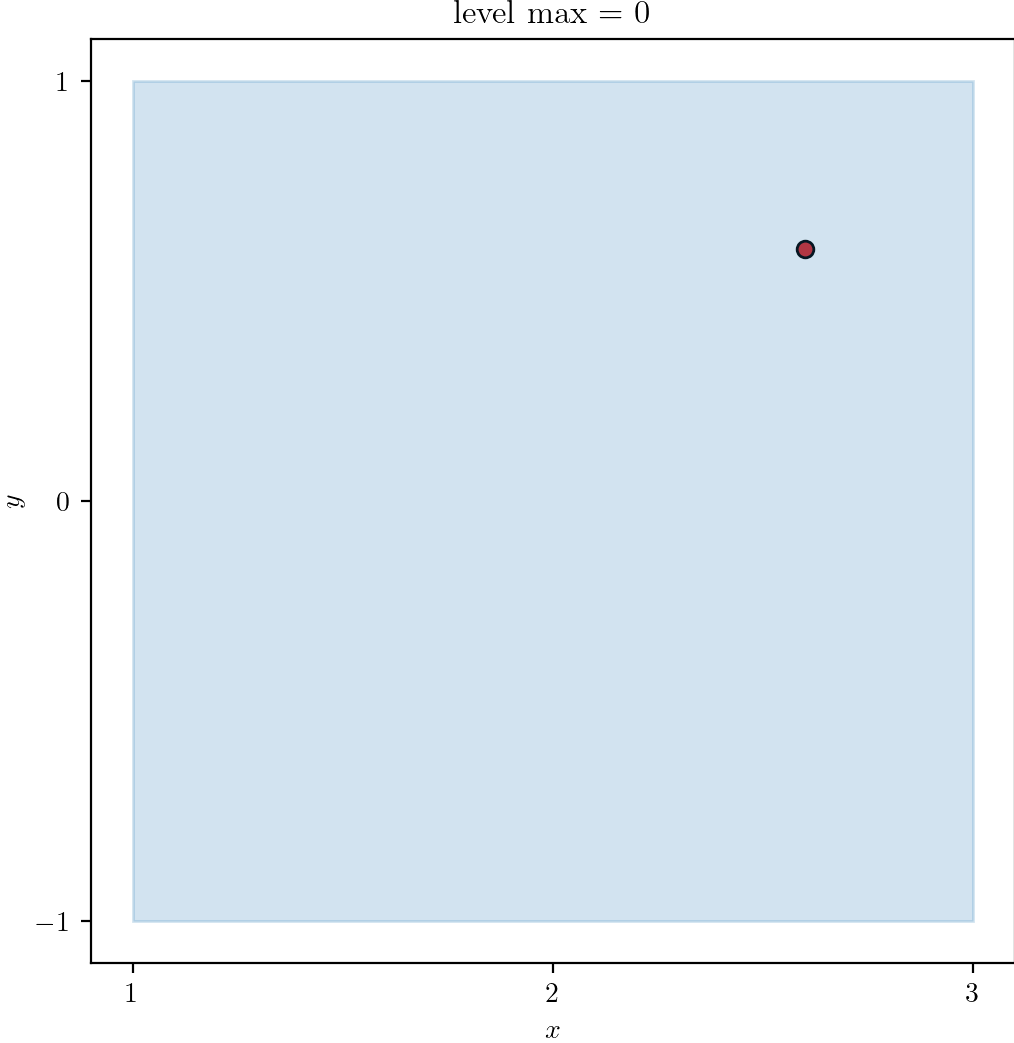
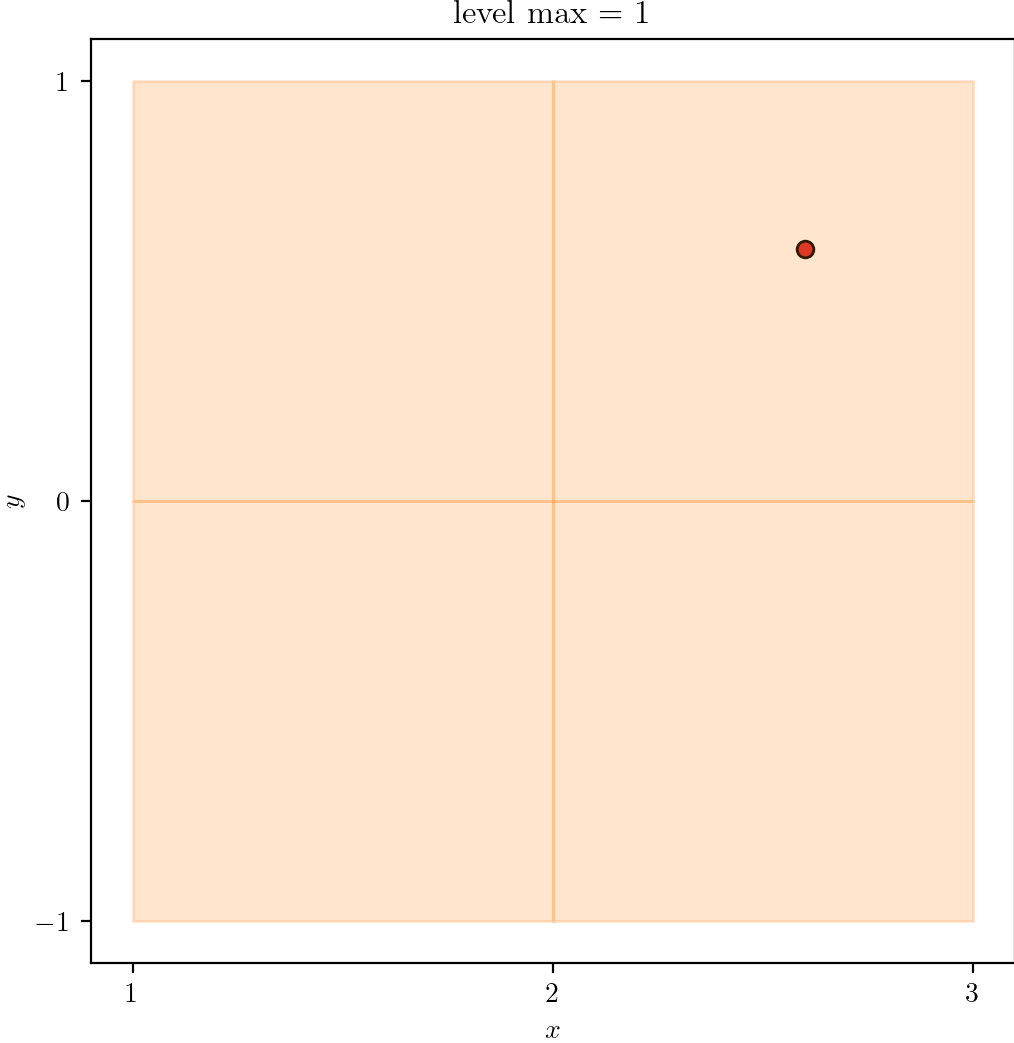
With plot_quadtree.py, we plot a domain

• A square domain L0 $$(x,y)\in ([1,3]\otimes [-1,1])$$
• Single point at (2.6, 0.6) to trigger refinement.

Level 0	1	2

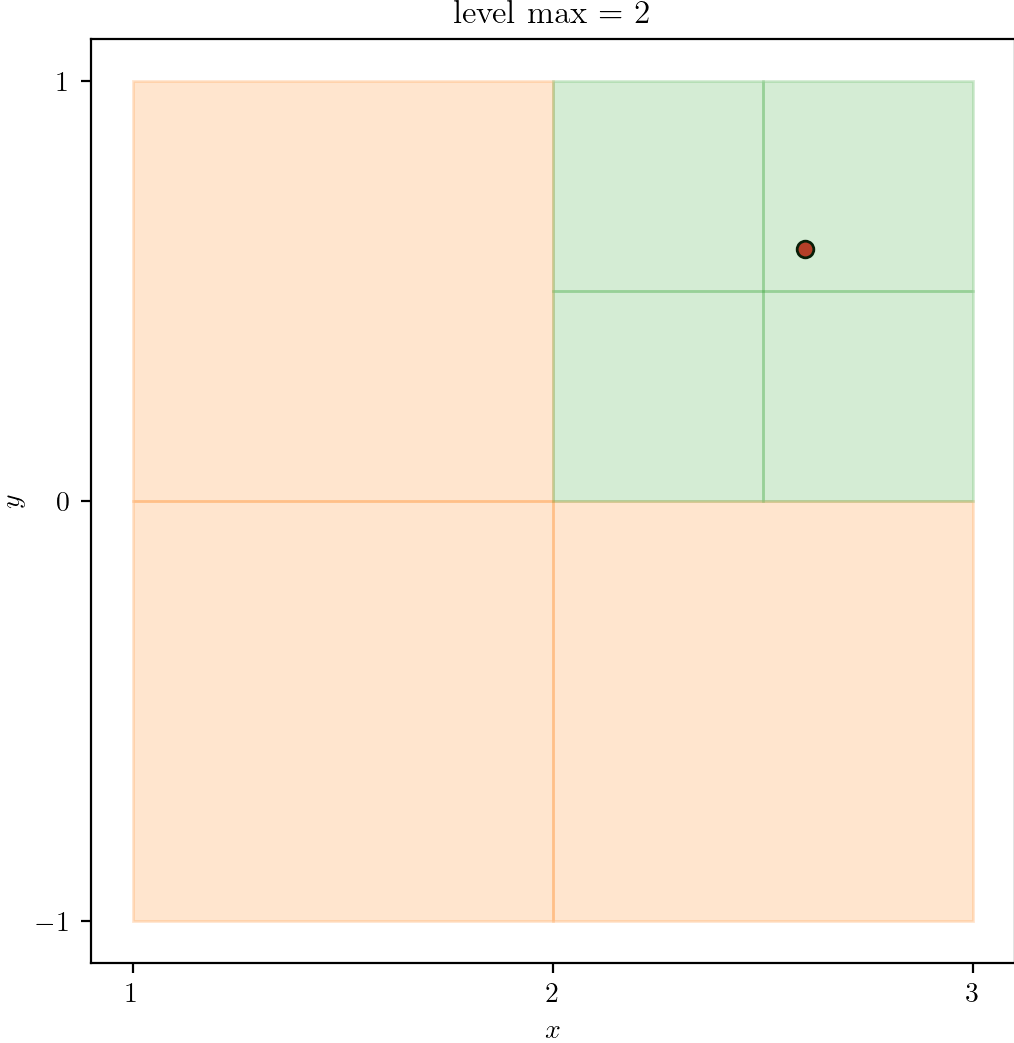3	4	5

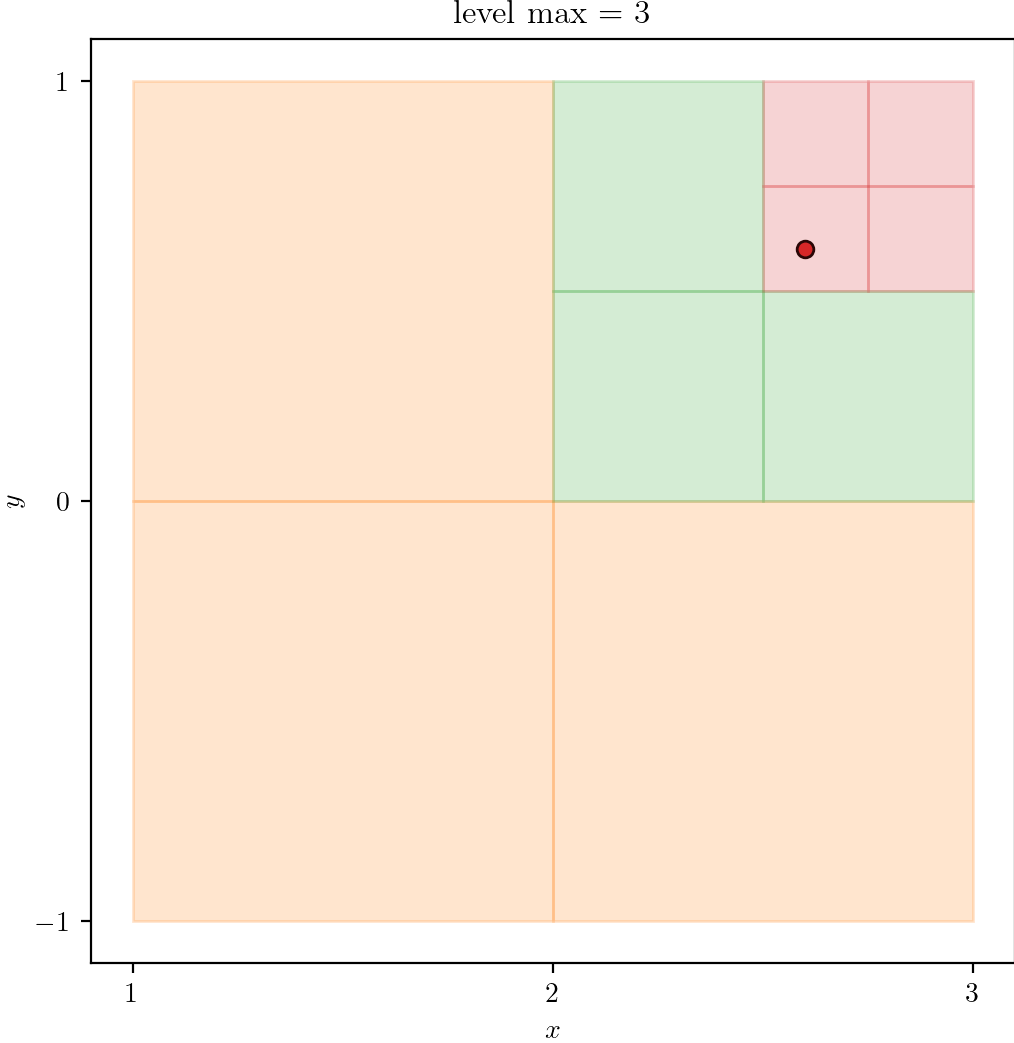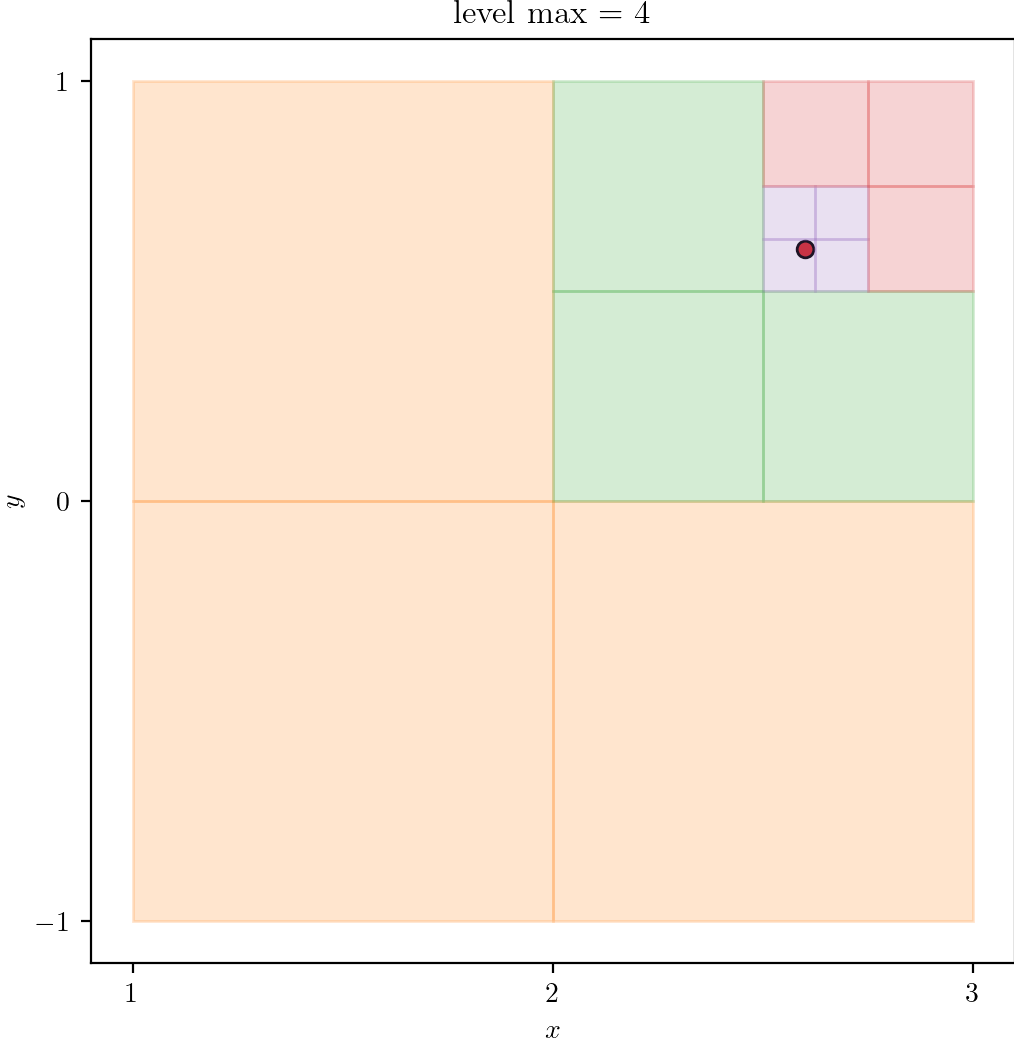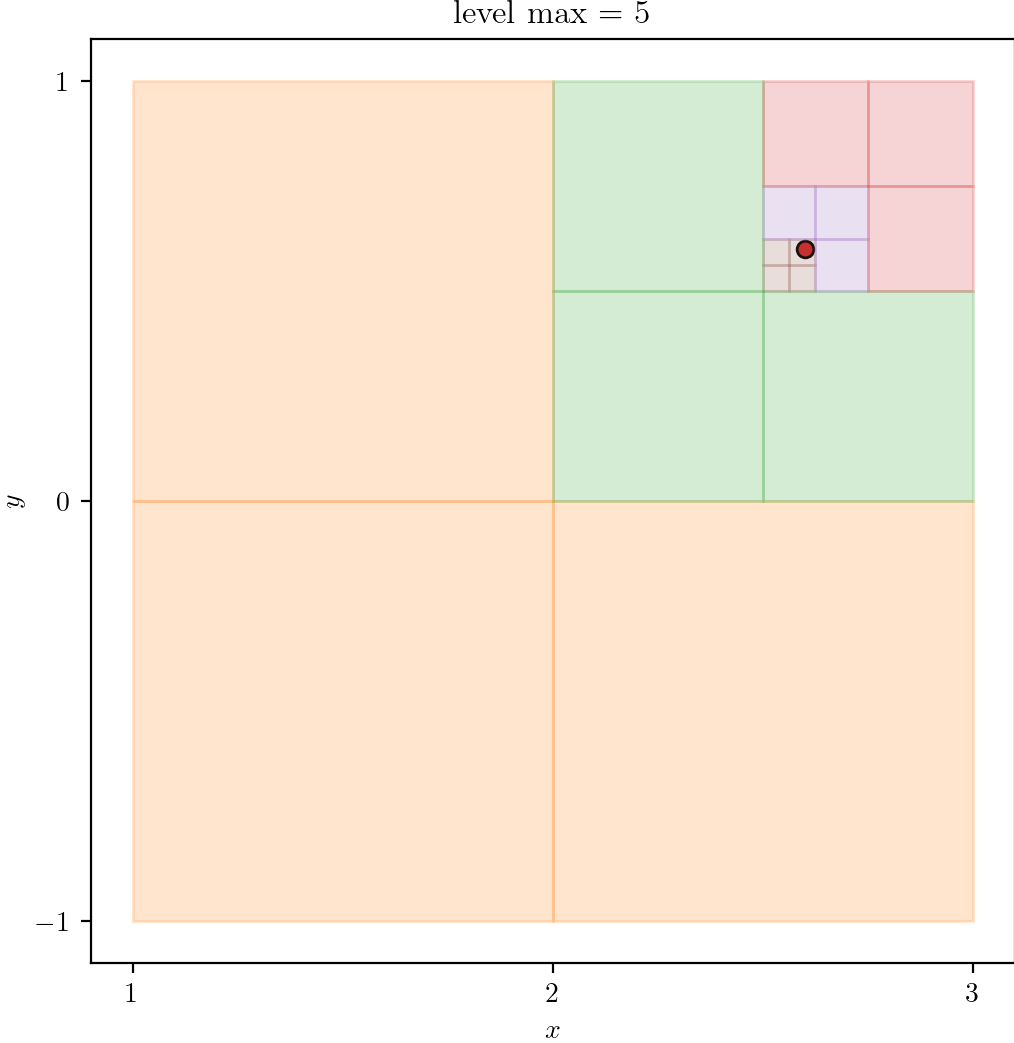Circle from Segmentation

We illustrate the segmentation start point as it applies to quadtree formation.

• For a segmentation at a given resolution of pixels, we immerse the segmentation into a single-cell (L0) quadtree domain.
• We pad the segmentation margins with void (segmentation ID 0) such that the pixel count in all directions ($x$ and $y$)
  • is the same, and
  • is divisible by 2 for $n$ cell subdivisions.
• For each cell in the quadtree, we process the cells recursively and ask this question: Does the cell contain more than one material? If yes, then subdivide; if no, then do not subdivide.

3	4	5	6

13	14	15	16

Circle from Boundary

We illustrate the boundary start point as it applies to quadtree formation.

• We define a boundary as directed series of connected, discrete points that create a closed-loop, non-intersecting path.
• We immerse the boundary into a single-cell (L0) quadtree domain.
• For each cell in the quadtree, we process the cells recursively and ask this question: Does the cell contain at least one boundary point? If yes, then subdivide; if no, then do not subdivide.

Consider a boundary of a circle defined by discrete (x, y) points.

Level 0	1	2

3	4	5

Circle from Tesellation

We illustrate the tesellation as it applies to quadtree formation.

• We immerse the tesellation into a single-cell (L0) quadtree domain.
• We create a boundary of the tesellation with points that lie on the boundary of the tesellation.
• We immerse the boundary into a single-cell (L0) quadtree domain.
• For each cell in the quadtree, we process the cells recursively and ask this question: Does the cell contain at least one boundary point? If yes, then subdivide; if no, then do not subdivide.

Quarter Plate

With Python, we produce a Quadtree with zero to five levels of refinement. Refinement is triggered based on whether or not a cell contains one or more seed points, shown as points along the quarter circle centered at (4, 0).

Level 0	1	2

3	4	5

Octree

Sphere

Consider a boundary of a sphere defined by a discrete triangular tesselation.

References

• https://github.com/sandialabs/sibl/blob/master/geo/doc/quadtree.md
• https://github.com/sandialabs/sibl/blob/master/geo/doc/dual_quad_transitions.md
• https://github.com/sandialabs/sibl/blob/master/geo/doc/dual/lesson_11.md

Source

quadtree_plot.py