Laplace Smoothing with Hierarchical Control
Laplace Smoothing, Hierarchical Control, Prescribed Homogeneous
Cube with Inclusion
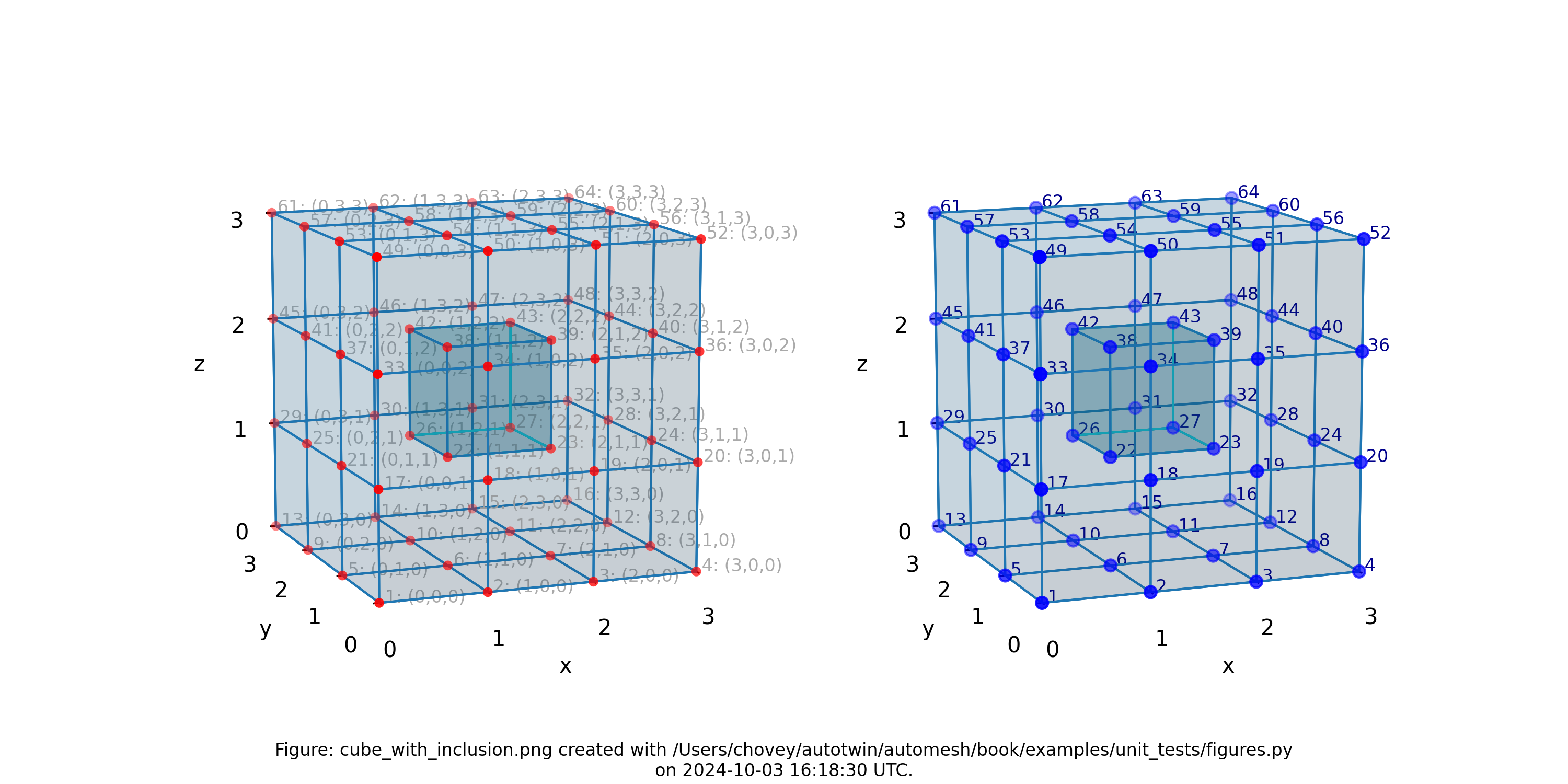
To come.
Laplace Smoothing, Hierarchical Control, Prescribed Inhomogeneous
Bracket
To begin to examine hiearchical control, we consider the Bracket example.

Figure: The Bracket example.
Laplace Smoothing without Hierarchical Control
As a baseline, let's examine what Laplace smoothing, , without hierarchical control performs.
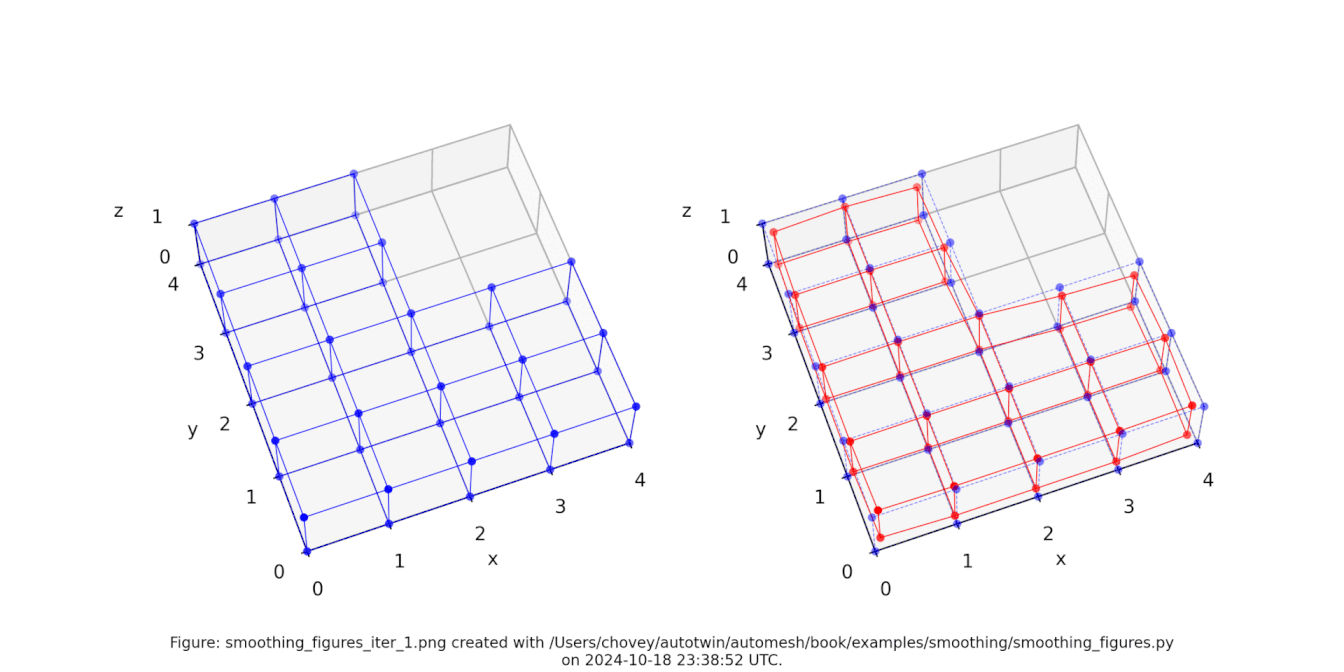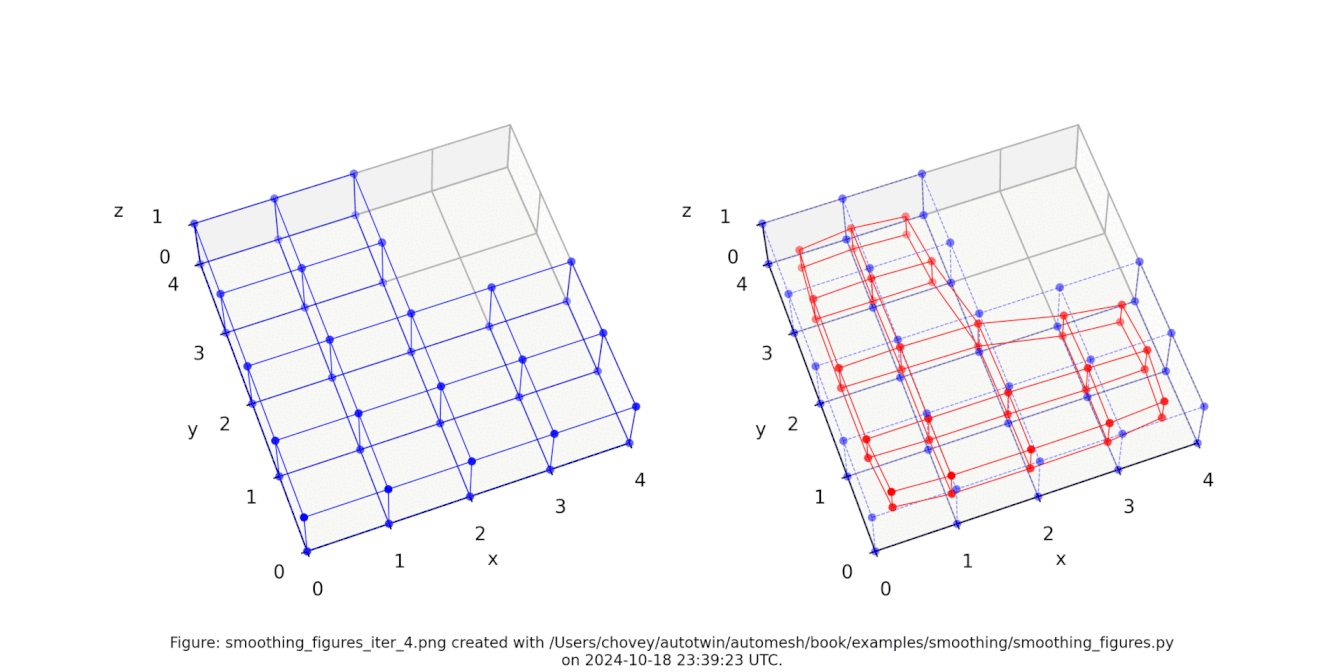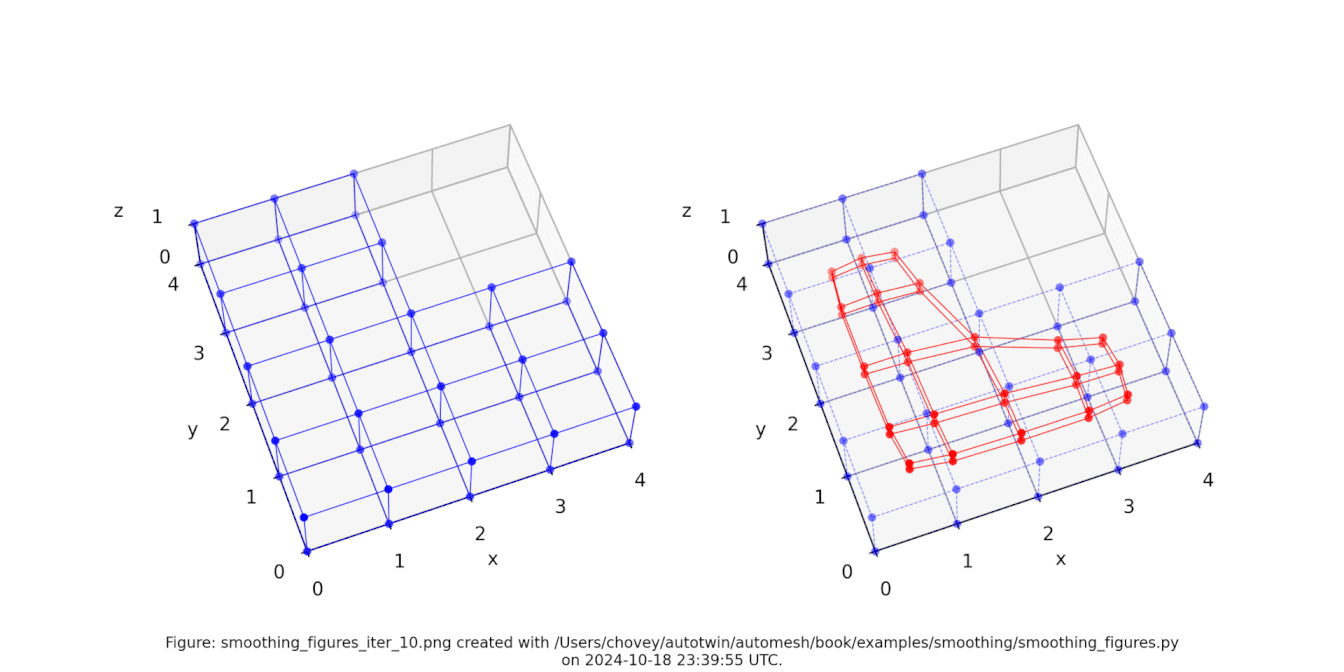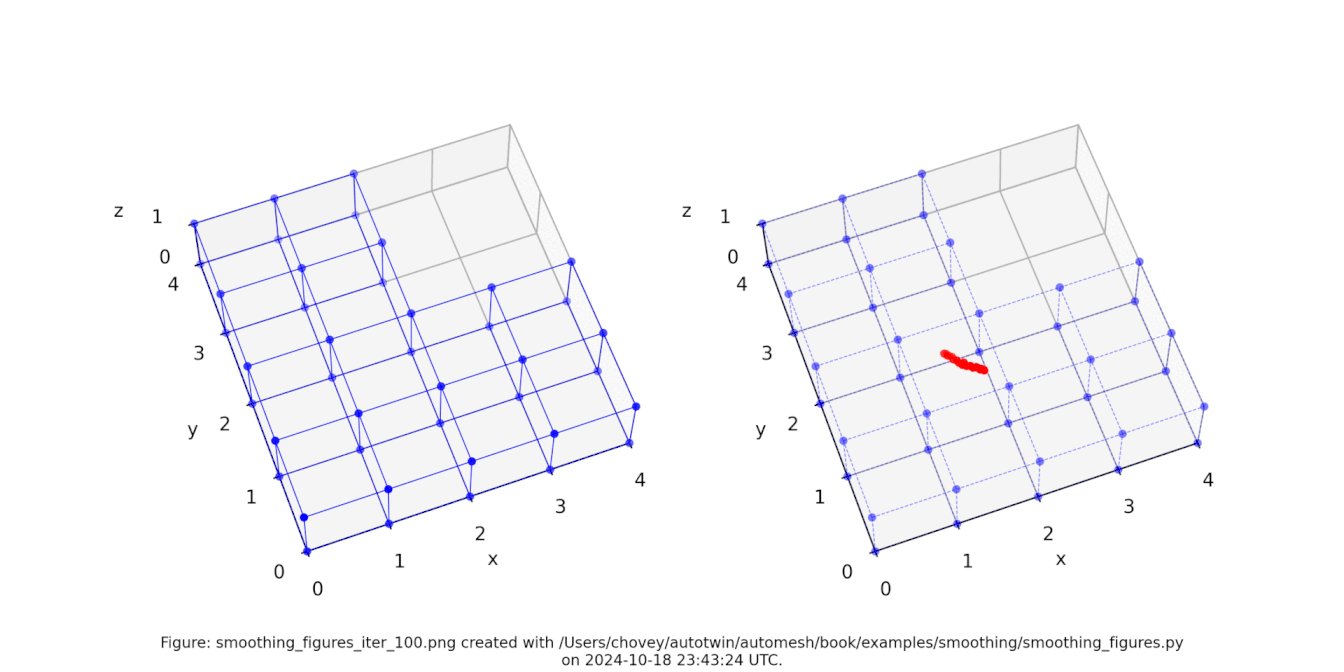
Figure: The Bracket test problem (left) original configuration, (right) subject to [1, 2, 3, 4, 5, 10, 20, 30, 100] iterations of Laplace smoothing. Animation created with Ezgif.
As an example, the nodal positions after 10 iterations are as follows:
| node | x | y | z |
|---|---|---|---|
| 1 | 0.6603416706977089 | 0.6603416706977089 | 0.42058348557613 |
| 2 | 1.164014406316456 | 0.5922705223353653 | 0.4003570849733875 |
| 3 | 1.9979372129260855 | 0.5706936094999626 | 0.39548539946279243 |
| 4 | 2.8325693635137097 | 0.5703120664922405 | 0.40180333889841546 |
| 5 | 3.332396179530681 | 0.6196854057408008 | 0.4228468310236131 |
| 6 | 0.5922705223353653 | 1.164014406316456 | 0.4003570849733875 |
| 7 | 1.129330412354556 | 1.129330412354556 | 0.3779268501553354 |
| 8 | 1.986117815900869 | 1.100245269915641 | 0.3744217105825115 |
| 9 | 2.8536168286772536 | 1.0284532492877596 | 0.3839611664938703 |
| 10 | 3.3805688588919414 | 1.007196857251266 | 0.40846995582593837 |
| 11 | 0.5706936094999626 | 1.9979372129260853 | 0.39548539946279243 |
| 12 | 1.100245269915641 | 1.986117815900869 | 0.37442171058251145 |
| 13 | 1.9089262792820898 | 1.90892627928209 | 0.3766933485101331 |
| 14 | 2.816962753463538 | 1.5457873563122884 | 0.3970154773256839 |
| 15 | 3.3296020281899956 | 1.409074280806729 | 0.42165070606234384 |
| 16 | 0.5703120664922405 | 2.8325693635137097 | 0.40180333889841546 |
| 17 | 1.0284532492877596 | 2.8536168286772536 | 0.3839611664938703 |
| 18 | 1.5457873563122884 | 2.816962753463538 | 0.3970154773256839 |
| 19 | 0.6196854057408008 | 3.332396179530681 | 0.4228468310236131 |
| 20 | 1.007196857251266 | 3.3805688588919414 | 0.40846995582593837 |
| 21 | 1.409074280806729 | 3.3296020281899956 | 0.42165070606234384 |
| 22 | 0.6603416706977089 | 0.6603416706977089 | 0.5794165144238701 |
| 23 | 1.164014406316456 | 0.5922705223353653 | 0.5996429150266126 |
| 24 | 1.9979372129260853 | 0.5706936094999626 | 0.6045146005372077 |
| 25 | 2.8325693635137097 | 0.5703120664922404 | 0.5981966611015848 |
| 26 | 3.332396179530681 | 0.6196854057408007 | 0.5771531689763871 |
| 27 | 0.5922705223353654 | 1.164014406316456 | 0.5996429150266126 |
| 28 | 1.129330412354556 | 1.129330412354556 | 0.6220731498446648 |
| 29 | 1.986117815900869 | 1.100245269915641 | 0.6255782894174887 |
| 30 | 2.8536168286772536 | 1.0284532492877596 | 0.6160388335061299 |
| 31 | 3.3805688588919414 | 1.0071968572512657 | 0.5915300441740619 |
| 32 | 0.5706936094999626 | 1.9979372129260853 | 0.6045146005372076 |
| 33 | 1.100245269915641 | 1.986117815900869 | 0.6255782894174885 |
| 34 | 1.90892627928209 | 1.9089262792820898 | 0.623306651489867 |
| 35 | 2.816962753463538 | 1.5457873563122881 | 0.6029845226743162 |
| 36 | 3.3296020281899956 | 1.409074280806729 | 0.5783492939376563 |
| 37 | 0.5703120664922404 | 2.8325693635137097 | 0.5981966611015848 |
| 38 | 1.0284532492877596 | 2.8536168286772536 | 0.6160388335061298 |
| 39 | 1.5457873563122884 | 2.816962753463538 | 0.6029845226743162 |
| 40 | 0.6196854057408007 | 3.332396179530681 | 0.5771531689763871 |
| 41 | 1.0071968572512657 | 3.3805688588919414 | 0.5915300441740617 |
| 42 | 1.409074280806729 | 3.3296020281899956 | 0.5783492939376562 |
Laplace Smoothing with Hierarchical Control
We illustrate the how hierarchical control affects the Laplace smoothing.
Conside the PRESCRIBED and BOUNDARY node hierarchy below:
node_hierarchy: NodeHierarchy = (
# hierarchy enum, node number, prescribed (x, y, z)
Hierarchy.PRESCRIBED, # 1 -> (0, 0, 0)
Hierarchy.PRESCRIBED, # 2 -> (1, 0, 0)
Hierarchy.PRESCRIBED, # 3 -> (2, 0, 0)
Hierarchy.PRESCRIBED, # 4 -> (3, 0, 0)
Hierarchy.PRESCRIBED, # 5 -> (4, 0, 0)
Hierarchy.PRESCRIBED, # 6 -> (0, 1, 0)
Hierarchy.BOUNDARY, # 7
Hierarchy.BOUNDARY, # 8
Hierarchy.BOUNDARY, # 9
Hierarchy.PRESCRIBED, # 10 -> (4.5*cos(15 deg), 4.5*sin(15 deg), 0)
Hierarchy.PRESCRIBED, # 11 -> *(0, 2, 0)
Hierarchy.BOUNDARY, # 12
Hierarchy.BOUNDARY, # 13
Hierarchy.BOUNDARY, # 14
Hierarchy.PRESCRIBED, # 15 -> (4.5*cos(30 deg), 4.5*sin(30 deg), 0)
Hierarchy.PRESCRIBED, # 16 -> (0, 3, 0)
Hierarchy.BOUNDARY, # 17
Hierarchy.BOUNDARY, # 18
Hierarchy.PRESCRIBED, # 19 -> (0, 4, 0)
Hierarchy.PRESCRIBED, # 20 -> (1.5, 4, 0)
Hierarchy.PRESCRIBED, # 21 -> (3.5, 4, 0)
#
Hierarchy.PRESCRIBED, # 22 -> (0, 0, 1)
Hierarchy.PRESCRIBED, # 23 -> (1, 0, 1)
Hierarchy.PRESCRIBED, # 24 -> (2, 0, 1)
Hierarchy.PRESCRIBED, # 25 -> (3, 0, 1)
Hierarchy.PRESCRIBED, # 26 -> (4, 0, 1)
Hierarchy.PRESCRIBED, # 27 -> (0, 1, 1)
Hierarchy.BOUNDARY, # 28
Hierarchy.BOUNDARY, # 29
Hierarchy.BOUNDARY, # 30
Hierarchy.PRESCRIBED, # 31 -> (4.5*cos(15 deg), 4.5*sin(15 deg), 1)
Hierarchy.PRESCRIBED, # 32 -> *(0, 2, 1)
Hierarchy.BOUNDARY, # 33
Hierarchy.BOUNDARY, # 34
Hierarchy.BOUNDARY, # 35
Hierarchy.PRESCRIBED, # 36 -> (4.5*cos(30 deg), 4.5*sin(30 deg), 1)
Hierarchy.PRESCRIBED, # 37 -> (0, 3, 1)
Hierarchy.BOUNDARY, # 38
Hierarchy.BOUNDARY, # 39
Hierarchy.PRESCRIBED, # 40 -> (0, 4, 1)
Hierarchy.PRESCRIBED, # 41 -> (1.5, 4, 1)
Hierarchy.PRESCRIBED, # 42 -> (3.5, 4, 1)
)
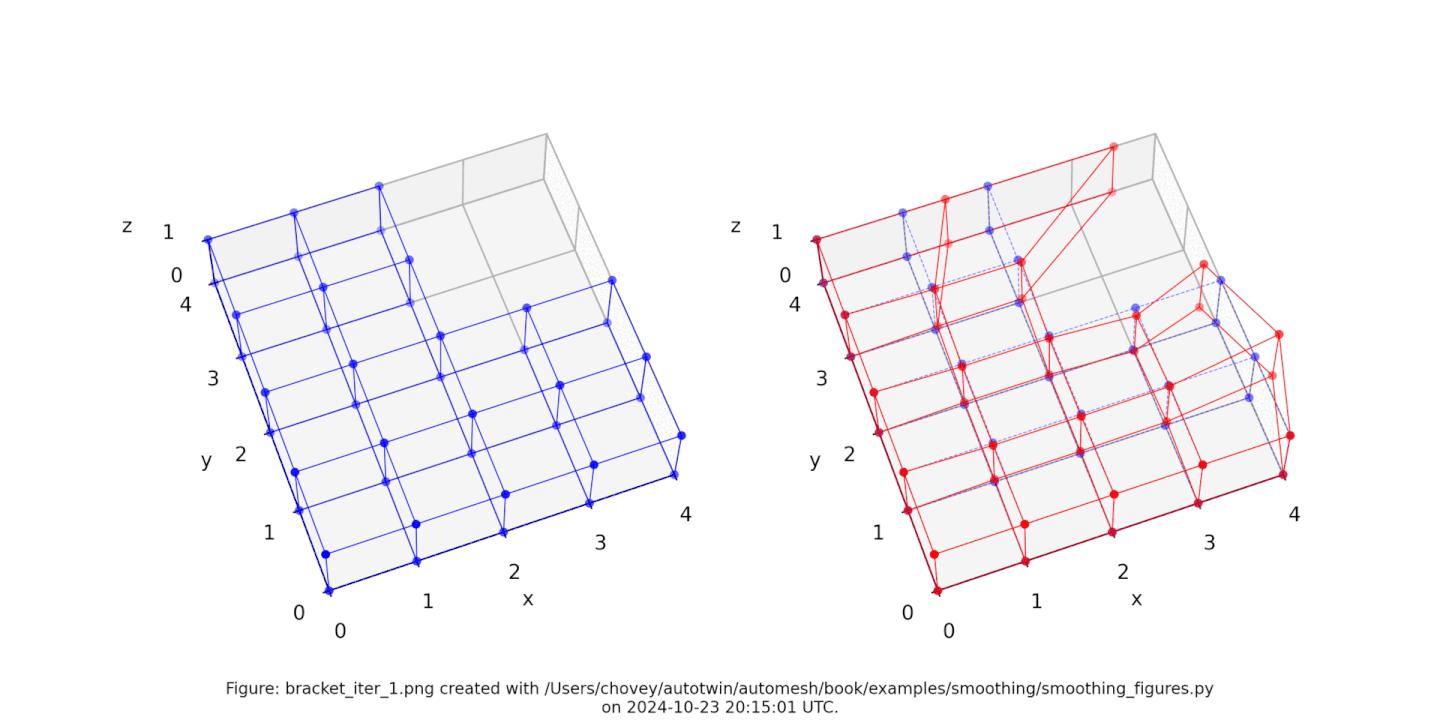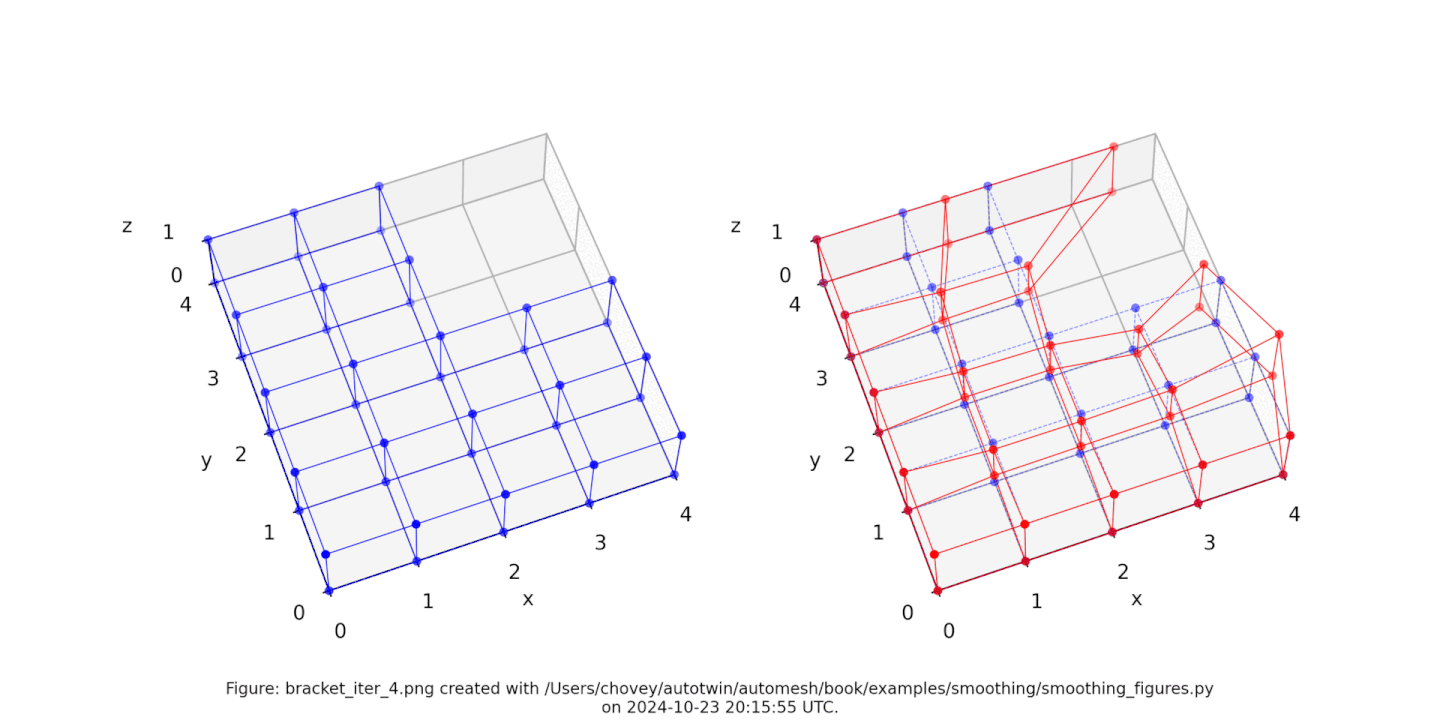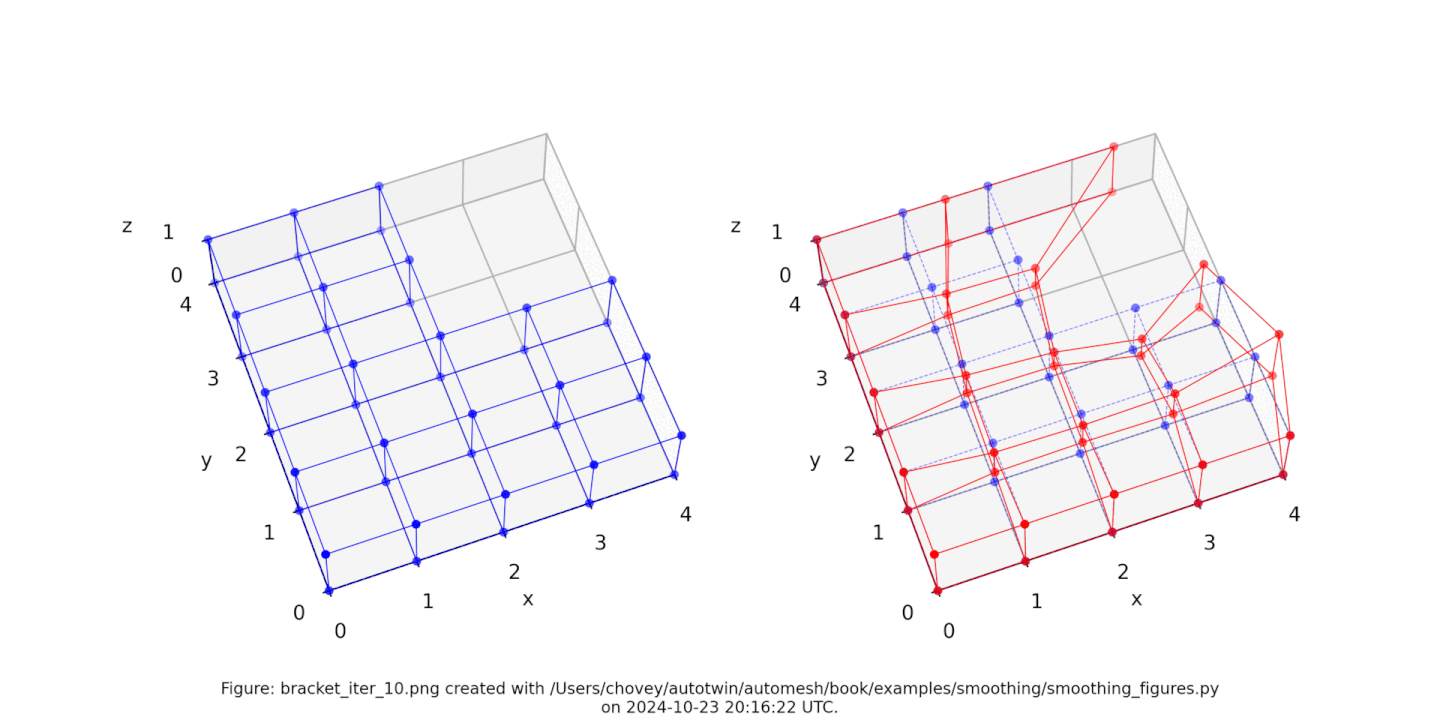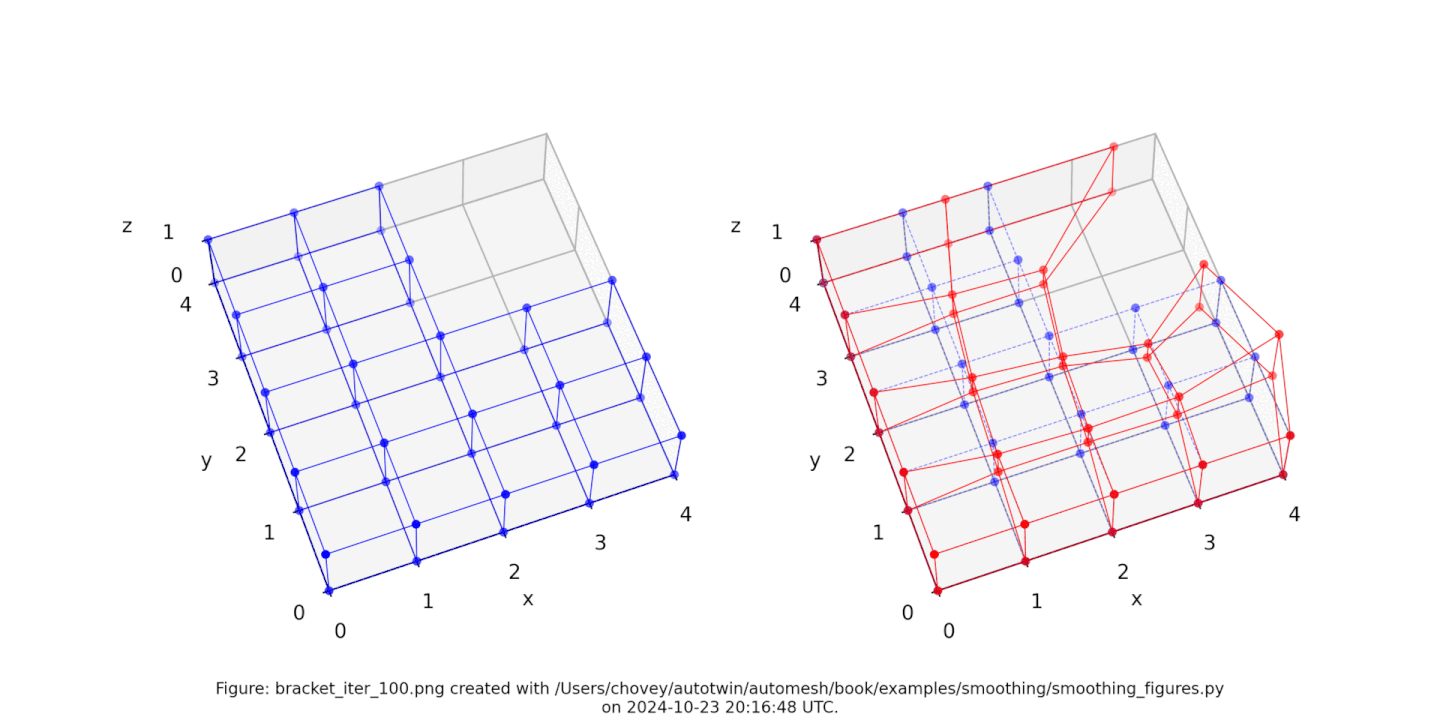
Figure: The Bracket test problem (left) original configuration, (right) subject to [1, 2, 3, 4, 5, 10, 20, 30, 100] iterations of Laplace smoothing with hierarchical control. Animation created with Ezgif.
As an example, the nodal positions after 10 iterations are as follows:
| node | x | y | z |
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| 2 | 1 | 0 | 0 |
| 3 | 2 | 0 | 0 |
| 4 | 3 | 0 | 0 |
| 5 | 4 | 0 | 0 |
| 6 | 0 | 1 | 0 |
| 7 | 1.0076218690550747 | 0.9988829259123082 | 0.24593434133370803 |
| 8 | 2.0218051968023 | 0.993985105791881 | 0.2837944855813176 |
| 9 | 3.0816593568068398 | 0.9931227966186256 | 0.24898414051620496 |
| 10 | 4.346666218300808 | 1.1646857029613433 | 0 |
| 11 | 0 | 2 | 0 |
| 12 | 1.0346002406957664 | 1.992982526945126 | 0.2837944855813176 |
| 13 | 2.0408618916639916 | 1.9528647520642073 | 0.3332231502067546 |
| 14 | 2.9955771790244468 | 1.7619821132207711 | 0.29909606343914835 |
| 15 | 3.897114317029974 | 2.2499999999999996 | 0 |
| 16 | 0 | 3 | 0 |
| 17 | 1.157261281731803 | 2.9982665159532105 | 0.24898414051620493 |
| 18 | 2.1973691292662734 | 2.991054895165017 | 0.29909606343914835 |
| 19 | 0 | 4 | 0 |
| 20 | 1.5 | 4 | 0 |
| 21 | 3.5 | 4 | 0 |
| 22 | 0 | 0 | 1 |
| 23 | 1 | 0 | 1 |
| 24 | 2 | 0 | 1 |
| 25 | 3 | 0 | 1 |
| 26 | 4 | 0 | 1 |
| 27 | 0 | 1 | 1 |
| 28 | 1.0076218690550747 | 0.9988829259123082 | 0.7540656586662919 |
| 29 | 2.0218051968023 | 0.993985105791881 | 0.7162055144186824 |
| 30 | 3.0816593568068398 | 0.9931227966186257 | 0.7510158594837951 |
| 31 | 4.346666218300808 | 1.1646857029613433 | 1 |
| 32 | 0 | 2 | 1 |
| 33 | 1.0346002406957664 | 1.9929825269451262 | 0.7162055144186824 |
| 34 | 2.0408618916639916 | 1.9528647520642073 | 0.6667768497932453 |
| 35 | 2.9955771790244468 | 1.7619821132207711 | 0.7009039365608517 |
| 36 | 3.897114317029974 | 2.2499999999999996 | 1 |
| 37 | 0 | 3 | 1 |
| 38 | 1.157261281731803 | 2.9982665159532105 | 0.751015859483795 |
| 39 | 2.1973691292662734 | 2.991054895165017 | 0.7009039365608516 |
| 40 | 0 | 4 | 1 |
| 41 | 1.5 | 4 | 1 |
| 42 | 3.5 | 4 | 1 |